В условиях научно-технического прогресса и постоянно растущего потока научной информации в образовательном процессе необходимыми шагами являются постоянный поиск новых эффективных форм обучения и переосмысление учебного материала с целью корректировки его подачи и объемов. Ясно также, что было приемлемо и целесообразно в образовании 20–30 лет назад, сегодня требует редакции. Главное при этом дать будущему специалисту фундаментальные знания и ограничить его от прослушивания второстепенных и малозначимых фактов теории, изучение которых может быть либо опущено вовсе, либо отдано на самостоятельную работу. Говоря точнее, учить надо тому, что является по-настоящему важным, трудным и актуальным. Второй немаловажной проблемой, стоящей сегодня в преподавании, является сокращение разрыва между учебным курсом, в данном случае курсом обыкновенных дифференциальных уравнений, и современным состоянием науки. Нельзя ограничиваться изложением научных фактов прошлого века, не знакомя с современными достижениями науки. Следующей проблемой является то, что по целому ряду объективных причин, сегодня на изучение обыкновенных дифференциальных уравнений (ОДУ) во многих технических вузах отводится, прямо скажем, недостаточно времени. На повестку дня встают два вопроса: чему учить и как, если в учебной программе предусмотрено 12–15 лекций и 15–20 практических занятий, а материал столь обширен. Ясно, что для таких втузов в сложившихся обстоятельствах необходима выработка новых концепций изложения, как теории ОДУ, так и практики.
Целью статьи является анализ проблем содержания курса дифференциальных уравнений втуза с малым количеством учебных часов и пути их решения, а также обоснование необходимости включения в тематические планы курсов математики втузов элементов качественного анализа нелинейных систем как важнейшего аппарата современной теории дифференциальных уравнений и нелинейной динамики.
Возможные пути решения проблем
Обсуждаемые проблемы многогранны, и все их аспекты нам не удастся обсудить. Остановимся на некоторых из них, относящихся к содержанию существующих учебных программ учебного курса ОДУ и выскажем некоторые критические замечания.
Курс ОДУ начинается с изучения уравнений первого порядка. Думается, что методы интегрирования дифференциальных уравнений первого порядка, сводящиеся к квадратурам, должны быть вынесены на практические занятия. На лекциях должны остаться общие вопросы теории уравнений первого порядка (типы уравнений, понятия о частном, общем и особом решениях, задачи, теоремы) и, возможно, ряд геометрических задач. На практике необходимо рассмотреть основные типы уравнений, но увлекаться интегрированием разных типов искусственно созданных примеров уравнений первого порядка, коих существует великое множество, также не следует. На лекциях при изложении дифференциальных уравнений высших порядков наряду с общей кратко изложенной теорией, должны найти отражение математические модели, за которыми стоят реальные физические процессы. На этих моделях надо демонстрировать понятия, задачи, утверждения, а также – приемы и методы исследования. Это позволит оживить изложение, более эффективно и рационально использовать учебное время и сблизить математику с ее инженерными приложениями. Тем самым на наш взгляд будет усилена и мотивация учащихся к изучению одного из центральных разделов математики. При этом здесь не идет речь о замене математики ее приложениями. В основной части изложение должно вестись строгим научным языком с использованием принятой научной лексики. Здесь наряду с основными понятиями и теоремами должны найти отражение: вопросы теории устойчивости решений, линеаризации уравнений, элементы теории бифуркаций, методы фазовой плоскости, малого параметра и усреднения, а также разностные схемы и дискретные отображения, т.е. те вопросы, которые естественным образом возникают при анализе любой технической задачи описываемой дифференциальными уравнениями. На наш взгляд, на математических кафедрах втузов для каждой специальности должны быть отобраны эталонные модели, изучение которых должно быть обязательным либо на лекциях, либо на практических занятиях. Определение таких моделей надо обсудить с преподавателями специальных кафедр на совместных совещаниях преподавательского состава. Например, для студентов электротехнического и радиотехнического профилей имеет смысл включить в тематические планы лекций и практических занятий исследование следующих математических моделей
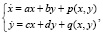
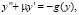
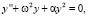
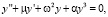
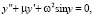
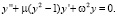
Эти модели чрезвычайно важны для формирования «нелинейного мышления» инженера. Их необходимо исследовать с учетом параметров и желательно разными методами: малого параметра, усреднения, фазовой плоскости. Такой объемный взгляд на одни и те же модели очень полезен и формирует глубокое знание. Кроме того, параллельно с теоретическим исследованием необходимо организовать и компьютерный практикум с целью выработки у студентов навыков моделирования решений на экране монитора с разными начальными данными и значениями параметров, а также исследованием дифференциальных систем, как в фазовом пространстве, так и в расширенном фазовом пространстве. Средства визуализации решений и траекторий, которые присутствуют в современных пакетах прикладных программ, несут неоспоримую помощь в освоении теории и реализуют эффективную обратную связь. Необходимо при этом помнить, что для будущего исследователя-прикладника инструментами должны выступать качественный анализ математической модели, вычислительный эксперимент, имитационное моделирование [1].
Что касается изложения теории линейных систем, то этот раздел необходимо изложить с особой тщательностью и полнотой, ибо к нему сводится огромное количество технических задач, и, кроме того, начальный этап исследования любой нелинейной задачи сводится к ее линеаризации, а следовательно, к линейной системе. Курс обыкновенных дифференциальных уравнений должен в обязательном порядке заканчиваться хотя бы кратким знакомством с некоторыми проблемами современной теории дифференциальных уравнений – с конкретными содержательными математическими примерами-моделями, над которыми работает современная наука.
Учитывая, что множество дифференциальных уравнений, допускающих интегрирование в замкнутом виде, мало, возрастает роль приближенных методов: численных, асимптотических и качественных. Эти последние методы в существующих учебных программах втузов отображены слабо. Именно на некоторых элементарных приемах качественного анализа дифференциальных уравнений мы и хотим остановиться далее подробнее. Желательно, чтобы приводимые ниже соображения нашли отражение и в общем курсе математики.
О качественном анализе в курсе ОДУ
Рассмотрим систему из n автономных обыкновенных дифференциальных уравнений, записанную в нормальной форме
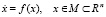. (1)
Здесь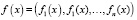 
– вектор правых частей, t – время,
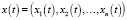– вектор неизвестных,
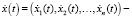вектор производных по времени t.
Предполагается, что функции fk(x) – непрерывно дифференцируемы в M и каждое решение системы (1) определено при всех t ≥ 0. Это предположение не является ограничительным, так как заменой времени в системе уравнений этого всегда можно достичь. Заметим, что, задание системы (1) эквивалентно заданию векторного поля f(x) на множестве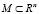 
.
Основы общего качественного анализа дифференциальных уравнений были заложены в конце XIX в. в трудах А. Пуанкаре и существенно продвинуты в части исследования устойчивости решений А.М. Ляпуновым [2, 3]. За последующие годы эта ветвь дифференциальных уравнений превратилась в мощный исследовательский аппарат. Продолжателями этой науки было получено множество важных результатов, изданы десятки монографий и учебников.
Идея качественных методов исследования дифференциальных уравнений весьма проста и заключается в исследовании свойств решений по структуре дифференциальных уравнений, не находя всей совокупности самих решений. Пуанкаре и Ляпунов первыми обратили внимание, что за основу новых методов нужно взять исследование векторного поля системы уравнений, так как поле порождает расслоение фазового пространства на траектории. А поле можно исследовать с помощью различных по конструкции дифференцируемых функций, поверхности уровня которых по отношению к полю являются трансверсальными – поле на которых направлено в одну сторону и не является касательным к ним. Эта геометрическая сторона качественной теории стала понятной, когда Ляпунов ввел понятие производной в силу системы дифференциальных уравнений от специально сконструированных функций, которые сегодня носят его имя. Позднее функции Ляпунова были обобщены, но их назначение осталось прежним – изучение поля, а следовательно, свойств всей совокупности решений, не занимаясь поиском самих решений.
Далее, не вдаваясь в теорию, на конкретном и чрезвычайно важном и познавательном примере излагаются некоторые приемы качественного исследования дифференциальных уравнений. Преследуется ознакомительная цель – введение в круг вопросов качественного анализа, при этом делается упор на те понятия, которые студентам первого и второго курса хорошо известны. Таким образом, малыми средствами делается введение в класс важных задач исследования математических моделей. Думается, что такой подход обоснован, учитывая малый ресурс времени, отводимый на изложение дифференциальных уравнений в общем курсе высшей математики втуза.
Приведем теперь некоторые определения из теории устойчивости [4–6].
Определение 1. Пусть система (1) имеет единственное положение равновесия x = a (f(a) = 0) – асимптотически устойчивое по Ляпунову. Система (1) называется устойчивой в целом если любое ее решение стремится к положению равновесия x = a.
Определение 2. Пусть в системе (1) несколько положений равновесия. Система (1) называется глобально асимптотически устойчивой, если любое ее решение стремится к некоторому положению равновесия.
Определение 3. Множество фазового пространства называется инвариантным, если оно состоит из целых траекторий.
Определение 4. Устойчивое положение равновесия и устойчивый предельный цикл называются аттракторами системы ОДУ.
Среди дифференциальных систем, описывающих физически важные процессы, особую роль играют системы, для которых выполняется следующее свойство: траектории с течением времени входят в некоторую замкнутую область G фазового пространства Rn и далее с течением времени не покидают ее. Такие системы в математической литературе называются диссипативными (диссипативными по Левинсону), а область G – областью диссипативности динамической системы (рис. 1). Сформулируем строгое определение.
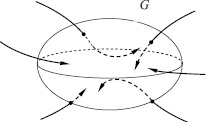
Рис. 1. Область диссипативности
Определение 5. Система (1) называется диссипативной [4], если для любого начального состояния x0∈Rn, найдется момент времени τ = τ(x0), такой, что при всех t ≥ τ выполняется включение x(t, x0)∈G. Отсюда, в частности, вытекает, что все решения системы определены на промежутке t ≥ 0 и нет решений, уходящих на бесконечность (решений типа «взрыва»).
Ясно, что доказательство диссипативности системы равносильно построению ее области диссипативности. При этом используются приемы, основанные на анализе векторного поля f(x) и заложенные во втором методе А.М. Ляпунова.
Опишем идею построения таких областей. Для этого зададимся функцией, из заданного класса, например из класса, положительно определенных квадратичных форм V(x) = (x, Ax). Здесь x∈Rn, A – симметричная квадратная n×n матрица. Поверхности уровня таких функций V(x) = c – const являются, как известно, вложенными эллипсоидами. Затем анализируется векторное поле f(x) системы на каждой из поверхностей. Если векторное поле системы ориентировано одинаково строго внутрь замкнутой области для всех поверхностей уровня c ≥ c0, то система диссипативна и можно утверждать, что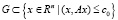 
.
Искусство нахождения такого семейства поверхностей связано с удачным выбором матрицы квадратичной формы А. Минимальное значение c0 определяется из условия касания поля f(x) поверхности уровня V(x) = c0 в некоторой точке.
Замечание. Аналитически установить точную конфигурацию области диссипативности G динамической системы, как правило, не удается. Однако ее оценка – множество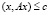 
полностью отвечает определению области диссипативности. Стремятся, как правило, найти ее лучшую оценку.
Для дальнейшего нам понадобится понятие производной от некоторой специальной функции V(x), в силу системы дифференциальных уравнений (1). История возникновения этих функций восходит к А.М. Ляпунову. Только у Ляпунова они знакоопределенные. Здесь же мы не будем этим ограничиваться. Таким образом, эти специальные функции являются обобщениями классических функций Ляпунова.
Определение 6. Пусть V(x), x∈Rn – дифференцируемая функция. Производной от функции V(x) в силу системы уравнений (1) называется
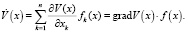(2)
Пример. Рассмотрим систему Э. Лоренца [7, 8]
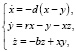(3)
где d > 0, b > 0 и r > 0 –параметры. Системе (3) посвящены десятки сотен статей, обзоров и книг в связи с открытием в 1960-х гг. сложного поведения траекторий, названного детерминированным хаосом. В связи с этим явлением множество работ было посвящено и оценкам ее области диссипативности [9, 10]. Далее мы приводим ряд простых утверждений, доказательства которых элементарны и доступны любому студенту знакомому с понятиями векторного поля, градиента, скалярного произведения векторов, критерием Сильвестра – знакоопределенности квадратичных форм.
Теорема 1. При r < 1 система (3) устойчива в целом, т.е. все ее траектории стремятся при t → +∞ к положению равновесия C0 (x = 0, y = 0, z = 0).
Доказательство. Рассмотрим положительно-определенную функцию
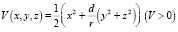(4)
и составим выражение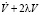 
, где λ – пока неопределенный параметр:
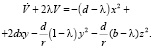
Потребуем, чтобы квадратичная форма, стоящая в правой части, была определенно-отрицательной. Следуя критерию Сильвестра это будет выполнено при
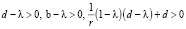. (5)
Пусть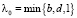 
. Тогда неравенства (5) будут выполнены, если λ∈(1, λ0). Таким образом, 
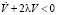при всех x, y, z кроме точки x = 0, y = 0, z = 0. Отсюда 
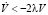. А так как V > 0, то 
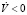. Последнее неравенство означает, что векторное поле на каждой из поверхностей V = С > 0, C = const направлено строго внутрь эллипсоида V = С. Это и доказывает утверждение теоремы.
Следствие. При r < 1 область диссипативности представляет собой точку C0.
При r > 1 – в системе (3) происходит первая бифуркация – положение равновесия C0 теряет устойчивость и из него рождаются два устойчивых
,
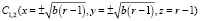(этот факт проверяется через линеаризацию системы (3) в окрестности положения равновесия) одновременно с этим рождается и нетривиальная область диссипативности, размеры и форма которой зависят от значений параметров d > 0, b > 0 и r > 1. Для построения области диссипативности системы (3) рассмотрим функцию
,
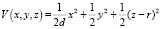заметив при этом, что поверхности уровня V = С этой функции представляют собой семейство эллипсоидов, и вычислим ее производную в силу системы (3):
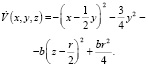
Ясно, что уравнение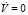 
также задает эллипсоид, причем для внутренних точек эллипсоида 
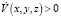, для точек вне эллипсоида 
.
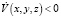Заметим, что условие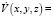 
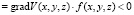геометрически означает, что векторное поле f(x, y, z) на поверхности V(x, y, z) = C направлено внутрь эллипсоида. Совершенно ясно, что если все поверхности V(x, y, z) = C > C0 будут содержать внутри себя эллипсоид 
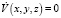, то областью диссипативности будет множество V(x, y, z) < C0, а это и доказывает, что система Лоренца (3) является диссипативной в смысле определения 2.
При доказательствах теорем теории устойчивости большую роль играют поверхности без контакта. Следующая теорема дает оценку области диссипативности снизу.
Теорема 2. При d > b имеют место следующие неравенства:
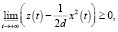(6)
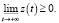(7)
Доказательство. Рассмотрим функцию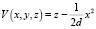 
и вычислим 
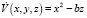. Во множестве 
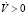рассмотрим цилиндрические поверхности V = C < 0. Они оказываются бесконтактными с направлением поля в полупространство V > C. А это и доказывает неравенство (6). Из (6) автоматически следует (7).
Теорема 3. При d = 2b система (3) глобально асимптотически устойчива.
Доказательству теоремы предпошлем следующие простые утверждения.
Лемма 1. При d = 2b система Лоренца имеет инвариантное множество, т.е. множество, состоящее из целых траекторий.
.
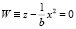Доказательство проводится непосредственной проверкой.
Лемма 2. При d = 2b система Лоренца на множестве W = 0 – глобально асимптотически устойчива.
Доказательство. Полагая в (3) d = 2b, получим, что третье уравнение становится тождественным первому. При этом полученная двумерная система описывает известное уравнение Дуффинга, глобально устойчивое при этих параметрах.
Доказательство теоремы 3 вытекает из лемм 1, 2 и того факта, что в области W > 0 выполняется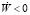 
, а в области W < 0 выполняется 
.
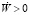На этом мы закончим обсуждение системы Лоренца. Отметим только, что она таит очень много интересных эффектов, среди которых есть явление странного аттрактора – инвариантного множества, которое, с одной стороны, притягивает все траектории и одновременно отталкивает их. При этом весь этот сложный сценарий разыгрывается как раз в области диссипативности, о существовании которой мы уже сказали выше. Почувствовать это понятие дифференциальных уравнений можно, если прибегнуть к численному эксперименту, впервые проделанному Э. Лоренцом в 1963 г. (рис. 2). Феномен странного аттрактора был обнаружен им при следующих значениях параметров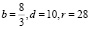 
.
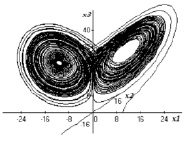
Рис. 2. Аттрактор Лоренца
Заключение
Подводя итог сказанному, зададимся вопросом. Должен ли курс обыкновенных дифференциальных уравнений быть универсальным для всех технических специальностей конкретного технического вуза? Возможно, да, если на его изложение отводится достаточное время. Однако проблема дефицита времени хорошо известна преподавателям высшей школы. Поэтому ответ на поставленный выше вопрос отрицательный. Объясняется это в первую очередь тем, что изложение теории чисто формально, строго, подробно и в общем виде не оставит времени на изложение важных математических моделей, рассмотрение которых необходимо сделать с точки зрения специальности, по которой происходит обучение. В силу сказанного мы рекомендуем во главу угла ставить не формальную теорию, а содержательные тщательно отобранные примеры, на которых и демонстрировать понятия, теорию, алгоритмы и приемы решения. Кроме того, не надо забывать, что студенческая аудитория технического вуза – это не аудитория будущих математиков. Для будущего инженера дифференциальные уравнения в первую очередь является инструментом исследования математических моделей объектов, технических систем, реальных процессов. При этом студент обретет определенную мотивацию к обучению, если он увидит хотя бы слабую, но связь лекционного материала и практических занятий со своей будущей специальностью или если он почувствует, что ему это в дальнейшем может пригодиться. В противном случае обучение будет малоэффективным, формальным и не будет способствовать главной цели – развитию творческого начала будущего специалиста. И последнее: учитывая, что класс дифференциальных уравнений, интегрируемых в замкнутом виде, ограничен, а многочисленные практические задачи приводят, как правило, к неинтегрируемым уравнениям, мы предлагаем в последней теме курса дифференциальных уравнений втузов включить изложение, хотя бы на элементарном уровне, элементов качественного анализа, позволяющих не интегрируя уравнения выносить суждение о свойствах решений, а это, как отмечалось выше, порой важнее знания самих решений.