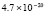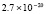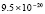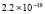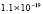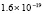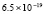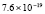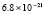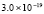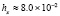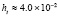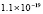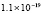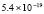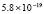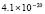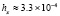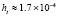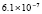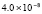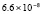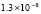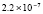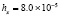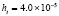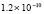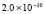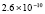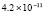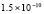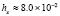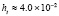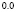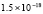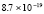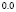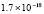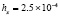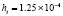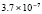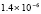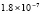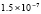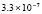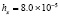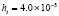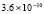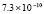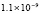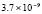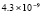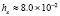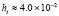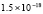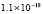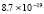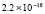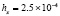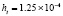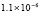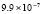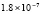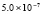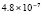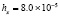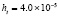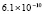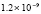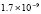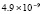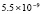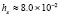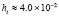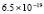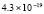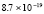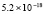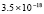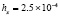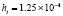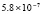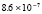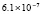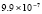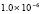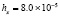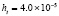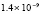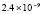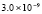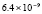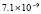Для уравнений в частных производных снижение погрешности приближенного решения является актуальной задачей. В частности, для уравнения переноса эта проблема обсуждается в [1–3]. Глубокому исследованию проблемы посвящены работы [4], где отмечается принципиальное значение уравнения переноса для численного решения нестационарных задач механики сплошной среды и задач газовой динамики. Границы погрешности существующих методов в прямоугольной области небольшого размера, в условиях гладкости решения, как правило, находятся в диапазоне 10–11–10-8. Для снижения погрешности в статье предлагается кусочно-интерполяционное решение задачи Коши для уравнения переноса с итерационным уточнением. Прототипом является представленный в [5] метод для случая обыкновенных дифференциальных уравнений. В случае уравнений в частных производных метод строится на основе интерполяционного полинома Ньютона от двух переменных, преобразуемого к виду алгебраического полинома с числовыми коэффициентами. Такая форма полинома позволяет естественным образом строить последовательные приближения для уточнения решения. В случае модельной одномерной задачи Коши для линейного уравнения переноса доказывается равномерная сходимость метода, оценивается скорость сходимости, для квазилинейного уравнения показана возможность аналогичных оценок. В [6] приведена программа и описан численный эксперимент, где рассматриваемая задача в прямоугольнике единичной высоты решается с погрешностью 10–19–10-18, ниже в статье приводятся результаты расширенного эксперимента. Схема построения метода формально допускает аналоги для разновидностей уравнений в частных производных, интегро-дифференциальных и интегральных уравнений.
В работе ставится цель построить численный метод решения уравнения переноса, который имеет следующие отличия от известных аналогов.
1. От разностных методов разрабатываемый метод отличается построением на основе интерполяционного полинома Ньютона для двух переменных с равноотстоящими по направлению осей декартовых координат узлами. Полином варьируемой степени строится в каждой прямоугольной подобласти, на которые делится исходная прямоугольная область, метод является кусочно-интерполяционным.
2. От интерполяционных аналогов метод отличается тем, что полином имеет форму алгебраического полинома с числовыми коэффициентами. Коэффициенты конструктивно вычисляются на основе восстановления по корням полинома с помощью формул, отличных от формул Виета.
3. На основе алгебраической формы выполняется табличное восстановление первообразной от полинома, интерполирующего правую часть уравнения. Первообразная подставляется в правую часть на место искомой переменной. Такие подстановки итерируются, в результате достигается итерационное уточнение приближенного решения, выполняемое по аналогии с последовательными приближениями Пикара.
4. Отличия дают положительное преимущество относительно известных методов приближенного решения уравнения переноса, позволяющее достигать сравнительного повышения точности приближения на несколько десятичных порядков.
Цель работы включает математическое обоснование метода, выполнение его алгоритмизации, помимо того, требуется представить численный эксперимент, наглядно иллюстрирующий перечисленные свойства предложенного метода.
Кусочно-интерполяционное вычисление функций двух переменных
В декартовой системе координат UXT кусочно-интерполяционное приближение действительной функции u = u(x, t) двух действительных переменных в прямоугольной области
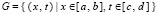 (1)
(1)
строится следующим образом. Область (1) разбивается на прямоугольные подобласти Gij с пересекающимися границами:
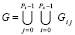 , (2)
, (2)
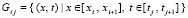 ,
,
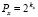 ,
, 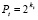 ,
, 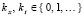 . (3)
. (3)
Интерполяционный полином Ньютона от двух переменных в подобласти (3) использует 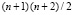 узлов с треугольным расположением:
узлов с треугольным расположением:
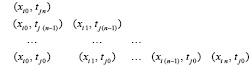 (4)
(4)
При расположении узлов (4) функция интерполируется в нижней треугольной части Gij, в верхней части фактически нужна экстраполяция, что учитывается в дальнейшем. Пусть произвольно задана граница ε абсолютной погрешности приближения функции u(x, t). В Gij интерполяционный полином Ньютона 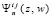 строится с равноотстоящими на шаги hx, ht по направлениям координат узлами
строится с равноотстоящими на шаги hx, ht по направлениям координат узлами  , где
, где
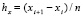 ,
, 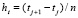 ,
, 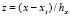 ,
, 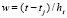 ,
, 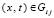 , (5)
, (5)
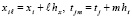 ,
, 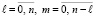 . (6)
. (6)
Искомый полином примет вид [7]
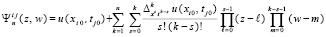 , (7)
, (7)
где 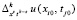 – конечные разности k-го порядка. Степень полинома n выбирается одинаковой для всех Gij и минимальной при условии
– конечные разности k-го порядка. Степень полинома n выбирается одинаковой для всех Gij и минимальной при условии
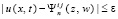
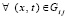 ,
,  . (8)
. (8)
Проверка точности приближения (8) в каждой подобласти выполняется на множестве точек 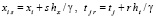 ,
, 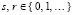 , где γ ≥ 3 – параметр. Минимальность n обеспечивается следующим образом. Построение и проверка точности начинаются с n = 1 и kx = 0, kt = 0 во всех Gij из (3). При нарушении неравенства (8) хоть в одной проверочной точке какой-либо подобласти значения kx и kt увеличиваются на единицу, и проверка начинается сначала. Процесс продолжается до нарушения априори заданных границ
, где γ ≥ 3 – параметр. Минимальность n обеспечивается следующим образом. Построение и проверка точности начинаются с n = 1 и kx = 0, kt = 0 во всех Gij из (3). При нарушении неравенства (8) хоть в одной проверочной точке какой-либо подобласти значения kx и kt увеличиваются на единицу, и проверка начинается сначала. Процесс продолжается до нарушения априори заданных границ 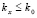 ,
, 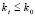 . Если в результате заданная точность не достигнута, то полагается kx = 0, kt = 0, степень n увеличивается на единицу и проверка возобновляется сначала для этой степени в тех же границах kx и kt. Описанный процесс циклически воспроизводится до нарушения априори заданной границы
. Если в результате заданная точность не достигнута, то полагается kx = 0, kt = 0, степень n увеличивается на единицу и проверка возобновляется сначала для этой степени в тех же границах kx и kt. Описанный процесс циклически воспроизводится до нарушения априори заданной границы 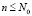 . В качестве искомого фиксируется наименьшее n, при котором неравенство (8) выполняется одновременно во всех проверочных точках всех
. В качестве искомого фиксируется наименьшее n, при котором неравенство (8) выполняется одновременно во всех проверочных точках всех 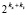 подобластей, в соответствии с этим фиксируются текущие значения kx и kt. Предполагается, что
подобластей, в соответствии с этим фиксируются текущие значения kx и kt. Предполагается, что 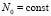 , но значения kx и kt абстрактно не ограничиваются. Полином (7) с видоизменением формул Виета [8] эквивалентно преобразуется к виду алгебраического полинома с числовыми коэффициентами
, но значения kx и kt абстрактно не ограничиваются. Полином (7) с видоизменением формул Виета [8] эквивалентно преобразуется к виду алгебраического полинома с числовыми коэффициентами
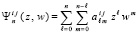 . (9)
. (9)
Значение (9) вычисляется по аналогии со схемой Горнера:
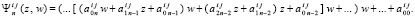
Для вычисления u(x, t), 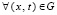 , дешифрируются индексы Gij:
, дешифрируются индексы Gij: 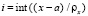 ,
, 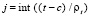 , int – целая часть числа,
, int – целая часть числа, 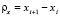 ,
, 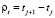 ,
, 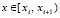 ,
, 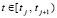 . Индексы определяют адрес массива коэффициентов полинома (9) в памяти компьютера, программа вычисления приводится в [6]. С целью оценки погрешности полином (7) рассматривается в эквивалентной форме
. Индексы определяют адрес массива коэффициентов полинома (9) в памяти компьютера, программа вычисления приводится в [6]. С целью оценки погрешности полином (7) рассматривается в эквивалентной форме
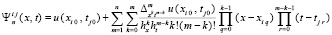 , (10)
, (10)
узлы интерполяции определяются из (5), (6). Сначала (10) рассматривается в области G, при этом не используются индексы подобласти. Остаточный член интерполяции в этом случае можно представить в виде [9]
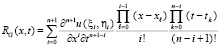 , (11)
, (11)
где 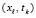 – узлы интерполяции,
– узлы интерполяции, 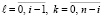 ,
, 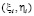 – некоторая точка внутри G. Если не оговорено иное, внутри области (подобласти) производные понимаются в обычном смысле, на границе – как односторонние производные по направлению изнутри к границе. Для дальнейшего предполагается существование, непрерывность, и, следовательно, ограниченность в замкнутой области G всех частных производных до порядка 2n + 1 включительно. Согласно (10) достаточно было бы ввести такое предположение относительно порядка n + 1. Смысл формального завышения порядка гладкости заключается в следующем. Вследствие треугольности расположения узлов (4) остаточный член (11) фактически относится только к нижней треугольной части, а не ко всей прямоугольной области G. Для оценки погрешности именно во всей области G преобразуется расположение узлов. Интерполяционный полином строится в описанном прямоугольном треугольнике, катеты которого продолжают нижнюю и левую стороны прямоугольника G, длина каждого катета вдвое больше продолжаемой стороны. Гипотенуза треугольника, охватывающего все узлы, пройдет через правую вершину G. В описанном треугольнике узлы (4) полностью охватят область G, остаточный член (11) будет распространяться на всю эту область. Аналогичное преобразование выполняется для каждой подобласти Gij. Вследствие преобразования расстояния hx, ht между узлами в (5), при неизменности степени полинома n, окажутся вдвое больше первоначально предполагавшихся в (5) значений. Чтобы не возросла погрешность, расстояния будут сохранены такими, как они были даны в (5), тогда степень интерполирующего полинома станет равной 2n. Это соответствует количеству
– некоторая точка внутри G. Если не оговорено иное, внутри области (подобласти) производные понимаются в обычном смысле, на границе – как односторонние производные по направлению изнутри к границе. Для дальнейшего предполагается существование, непрерывность, и, следовательно, ограниченность в замкнутой области G всех частных производных до порядка 2n + 1 включительно. Согласно (10) достаточно было бы ввести такое предположение относительно порядка n + 1. Смысл формального завышения порядка гладкости заключается в следующем. Вследствие треугольности расположения узлов (4) остаточный член (11) фактически относится только к нижней треугольной части, а не ко всей прямоугольной области G. Для оценки погрешности именно во всей области G преобразуется расположение узлов. Интерполяционный полином строится в описанном прямоугольном треугольнике, катеты которого продолжают нижнюю и левую стороны прямоугольника G, длина каждого катета вдвое больше продолжаемой стороны. Гипотенуза треугольника, охватывающего все узлы, пройдет через правую вершину G. В описанном треугольнике узлы (4) полностью охватят область G, остаточный член (11) будет распространяться на всю эту область. Аналогичное преобразование выполняется для каждой подобласти Gij. Вследствие преобразования расстояния hx, ht между узлами в (5), при неизменности степени полинома n, окажутся вдвое больше первоначально предполагавшихся в (5) значений. Чтобы не возросла погрешность, расстояния будут сохранены такими, как они были даны в (5), тогда степень интерполирующего полинома станет равной 2n. Это соответствует количеству 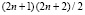 узлов в их преобразованном расположении. В дальнейших оценках и в соотношениях вида (7)–(11) n всегда будет заменяться на 2n. С данными изменениями имеет место соотношение
узлов в их преобразованном расположении. В дальнейших оценках и в соотношениях вида (7)–(11) n всегда будет заменяться на 2n. С данными изменениями имеет место соотношение
 . (12)
. (12)
Неравенство (12) получается следующим образом. Если для точки (x, t) из (11) в слагаемом под знаком Σ (c заменой n на 2n) выполняется 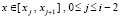 ,
, 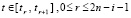 , то
, то
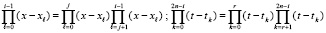 .
.
Поэтому
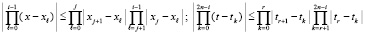 .
.
Отсюда
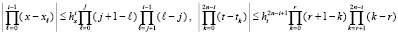 ,
,
или,
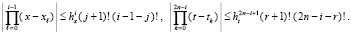
С учетом 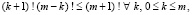 получится
получится
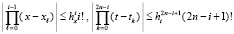 .
.
С другой стороны, если для (x, t) в рассматриваемом слагаемом с индексом i0, 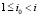 , под знаком Σ выполняется
, под знаком Σ выполняется 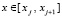 ,
, 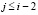 , но
, но 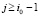 , то
, то 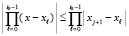 . Поэтому
. Поэтому 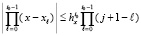 , следовательно,
, следовательно, 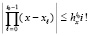 . Если под знаком Σ в (11) с рассматриваемым видоизменением
. Если под знаком Σ в (11) с рассматриваемым видоизменением 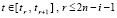 , но для i0,
, но для i0, 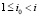 , выполняется
, выполняется 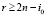 , то
, то 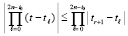 . Поэтому
. Поэтому 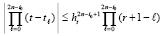 , следовательно,
, следовательно, 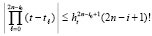 . В результате
. В результате
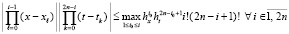 .
.
Тем более,
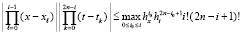 . (13)
. (13)
Неравенство (13) сохраняется в случае i = 0 и выполняется 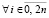 . Из (11) (при замене n на 2n)
. Из (11) (при замене n на 2n)
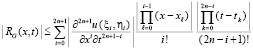 . (14)
. (14)
В рассматриваемых предположениях
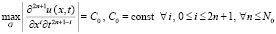 . (15)
. (15)
Подстановка в (14) правых частей из (13) и C0 из (15) влечет (12). Всюду ниже предполагается, что размеры G позволяют считать расстояния между узлами меньшими единицы при всех рассматриваемых n. Узлы являются равноотстоящими вдоль направлений осей, поэтому найдутся h, q, p, такие, что
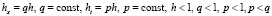 . (16)
. (16)
Из (12) и (16) 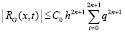 . Очевидно,
. Очевидно, 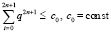 . В обозначении
. В обозначении 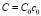 ,
,
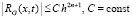 . (17)
. (17)
Пусть теперь по этой же схеме в каждой подобласти Gij построен интерполяционный полином (10) с заменой показателя степени n на 2n. Тогда расстояния между проекциями узлов на оси координат уменьшатся соответственно в обратной пропорции 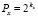 и
и 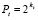 , где kx, kt из (3). В (12) тех же пропорциях соответственно уменьшатся hx, ht, поэтому
, где kx, kt из (3). В (12) тех же пропорциях соответственно уменьшатся hx, ht, поэтому 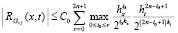 . Если выбрать
. Если выбрать 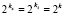 , то h в (17) обратно пропорционально 2k, в результате
, то h в (17) обратно пропорционально 2k, в результате
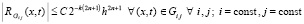 . (18)
. (18)
В (18) C, h из (17), h < 1, i, j из (2). Таким образом, имеет место
Лемма 1. Пусть функция u(x, t) определена в G из (1), где у нее существуют и непрерывны все частные производные до порядка 2n + 1 включительно. Тогда при условии разбиения G на 22k подобластей (2), (3) в случае 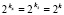 , кусочно-интерполяционное приближение данной функции в G с помощью полиномов вида (7), взятых в степени 2n, может быть выполнено с абсолютной погрешностью (18), где шаги интерполяции hx, ht из (5) связаны с h < 1 из (17) соотношениями (16).
, кусочно-интерполяционное приближение данной функции в G с помощью полиномов вида (7), взятых в степени 2n, может быть выполнено с абсолютной погрешностью (18), где шаги интерполяции hx, ht из (5) связаны с h < 1 из (17) соотношениями (16).
Рассматриваемое приближение инвариантно относительно i, j из (2), (3), поэтому в левой части (18) можно взять максимум по всем подобластям:
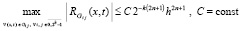 . (19)
. (19)
Отсюда вытекает
Теорема 1. В условиях леммы 1 кусочно-интерполяционное приближение равномерно сходится к функции u(x, t) в области G при k → ∞ со скоростью сходимости (19).
В каждой подобласти полином (7) может быть преобразован к виду (9) со степенью 2n без изменения оценок (18), (19). В дальнейшем используются соотношения
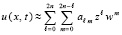 ,
, 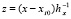 ,
, 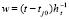 , (20)
, (20)
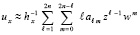 ,
, 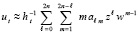 , (21)
, (21)
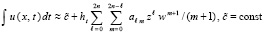 . (22)
. (22)
Значения констант и параметров определяются по ходу изложения, hx, ht в (20)–(22) пропорциональны h согласно (16).
Исходные предположения
Вначале рассматривается задача Коши для линейного уравнения
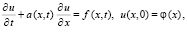 (23)
(23)
где a(x, t), f(x, t) – заданные функции, рассматриваемые в полуплоскости 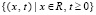 , φ(x) – заданная функция
, φ(x) – заданная функция 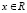 [4]. Для построения метода приближенного решения выбраны прямоугольная область задания этих функций и одна из ее границ, определяемые непосредственно ниже. Ввиду применения кусочной интерполяции с оценками (14), (19) для анализа сходимости используются следующие ограничения.
[4]. Для построения метода приближенного решения выбраны прямоугольная область задания этих функций и одна из ее границ, определяемые непосредственно ниже. Ввиду применения кусочной интерполяции с оценками (14), (19) для анализа сходимости используются следующие ограничения.
I. Приближенное решение задачи (23) строится в области G из (1), объединяющей подобласти Gij из (2), (3) при 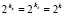 , областью определения φ(x) служит основание G на оси OX. Значения a и b не конкретизируются, вместе с тем всюду ниже c = 0, d = T,
, областью определения φ(x) служит основание G на оси OX. Значения a и b не конкретизируются, вместе с тем всюду ниже c = 0, d = T, 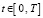 . Предполагается, что u(x, t) принадлежит области
. Предполагается, что u(x, t) принадлежит области 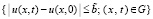 , где
, где 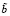 – постоянная, значение которой может быть задано произвольно, при необходимости оно конкретно оговаривается.
– постоянная, значение которой может быть задано произвольно, при необходимости оно конкретно оговаривается.
II. Предполагается, что в области 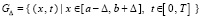 , при
, при 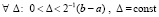 , существуют и непрерывны все частные производные u(x, t) до порядка 2n + 1 включительно
, существуют и непрерывны все частные производные u(x, t) до порядка 2n + 1 включительно 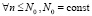 , с таким же порядком непрерывно дифференцируемы a(x, t) и f(x, t), функция φ(x) определена и непрерывно дифференцируема 2n + 1 раз на отрезке
, с таким же порядком непрерывно дифференцируемы a(x, t) и f(x, t), функция φ(x) определена и непрерывно дифференцируема 2n + 1 раз на отрезке 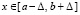 .
.
III. Предполагается, что в подобласти 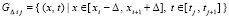 значение Δ может быть произвольным в границах
значение Δ может быть произвольным в границах 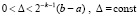 .
.
В предположениях I, II обусловлено существование и единственность, а также устойчивость решения задачи (23) относительно возмущения начальных данных [4].
В Gij приближенное решение строится с помощью интерполяционного полинома с итерационным уточнением, последовательно по j выполняется переход от Gij к Gi(j+1). За начальные условия в Gi(j+1) принимается приближение из Gij на смежной с Gi(j+1) границе. В G00 узловые значения интерполяции задает функция φ(x). Конкретно интерполируется 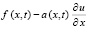 , что дает приближение
, что дает приближение 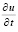 . Интеграл по времени от интерполяционного полинома принимается за приближение решения, которое подставляется в выражение
. Интеграл по времени от интерполяционного полинома принимается за приближение решения, которое подставляется в выражение 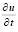 из (23). Полученное приближение
из (23). Полученное приближение 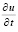 снова интерполируется, и описанный процесс повторяется с использованием (20)–(22). На практике итерации выполняются до искомой точности приближения, абстрактно их количество предполагается неограниченным. Процесс воспроизводится в каждой подобласти до полного прохода области G.
снова интерполируется, и описанный процесс повторяется с использованием (20)–(22). На практике итерации выполняются до искомой точности приближения, абстрактно их количество предполагается неограниченным. Процесс воспроизводится в каждой подобласти до полного прохода области G.
Итерационное уточнение с учетом остаточных членов интерполяции. В Gij
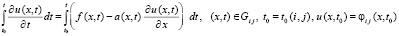 . (24)
. (24)
В дальнейшем обозначения корректируются с целью отличия от использованных при описании интерполяции функции. К нижним индексам полинома 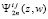 из (20) добавлен индекс 2k в соответствии с числом подобластей 22k, аналогичная индексация применяется к другим выражениям. Полином
из (20) добавлен индекс 2k в соответствии с числом подобластей 22k, аналогичная индексация применяется к другим выражениям. Полином 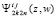 интерполирует не u(x, t), а подынтегральную функцию правой части (24), что отмечается слитным индексом ∂u, остаточный член интерполяции
интерполирует не u(x, t), а подынтегральную функцию правой части (24), что отмечается слитным индексом ∂u, остаточный член интерполяции 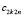 оценивается из (19), –
оценивается из (19), –
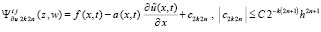 , (25)
, (25)
где z, w из (20), 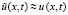 – приближение решения на предыдущей итерации. Аналогично (20),
– приближение решения на предыдущей итерации. Аналогично (20), 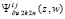 преобразуется к виду (9). Решение на текущей итерации приближается интегралом от
преобразуется к виду (9). Решение на текущей итерации приближается интегралом от 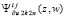 , определяемым аналогично (22). Полученный полином обозначается
, определяемым аналогично (22). Полученный полином обозначается 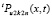 – по степени 2n, числу подобластей 22k и приближению u(x, t) путем интегрирования по t полинома
– по степени 2n, числу подобластей 22k и приближению u(x, t) путем интегрирования по t полинома 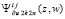 . Итерационный процесс примет вид
. Итерационный процесс примет вид
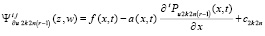 ,
,
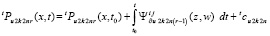 ,
,
где 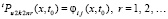 ,
, 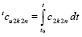 – остаточный член от приближения u(x, t) полиномом
– остаточный член от приближения u(x, t) полиномом 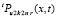 на отдельно взятой итерации. С учетом (25)
на отдельно взятой итерации. С учетом (25) 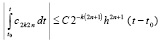 , согласно предположению II
, согласно предположению II 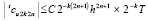 . Без явного выражения
. Без явного выражения 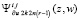 этот же процесс запишется в виде
этот же процесс запишется в виде
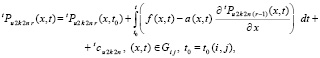 (26)
(26)
где 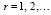 , коэффициенты
, коэффициенты 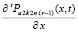 связаны с коэффициентами
связаны с коэффициентами  согласно (21), остаточный член оценивается из соотношения
согласно (21), остаточный член оценивается из соотношения
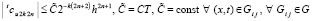 . (27)
. (27)
Пусть прямоугольник Gij произвольно фиксирован и уравнение (24) рассматривается в нем с теми же начальными условиями на границе, с которыми выполняются итерации (26). В этом случае решение не является точным, что отмечается чертой сверху, аналогично отмечается приближающий его полином, из (26) следует
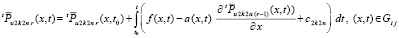 , (28)
, (28)
где использовано 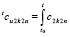 ,
, 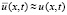 ,
, 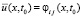 ,
, 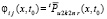 ,
, 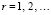
В предположениях I, II u(x, t) удовлетворяет соотношению
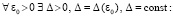
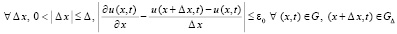 , (29)
, (29)
в частности (29) выполняется в случае Δx = Δ. В самом деле, по теореме о среднем, 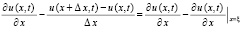 ,
, 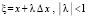 . Повторное применение теоремы влечет
. Повторное применение теоремы влечет 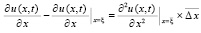 ,
, 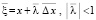 ,
, 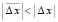 . Отсюда
. Отсюда 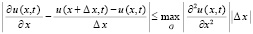 . Область G замкнута, поэтому
. Область G замкнута, поэтому 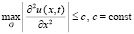 . Очевидно,
. Очевидно, 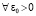 достаточно взять любое Δ = const,
достаточно взять любое Δ = const, 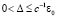 , чтобы выполнялось (29). Значение Δ в (29) можно произвольно уменьшить.
, чтобы выполнялось (29). Значение Δ в (29) можно произвольно уменьшить.
Для исследования сходимости (28) рассматривается вспомогательная задача
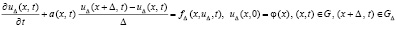 , (30)
, (30)
где 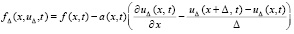 , f(x, t) из (23), Δ произвольно выбрано в соответствии с (29) и зафиксировано. Задача (30) является эквивалентным преобразованием (23), в области G решения задач совпадают и одновременно устойчивы к возмущению начальных данных. В предположениях I, II
, f(x, t) из (23), Δ произвольно выбрано в соответствии с (29) и зафиксировано. Задача (30) является эквивалентным преобразованием (23), в области G решения задач совпадают и одновременно устойчивы к возмущению начальных данных. В предположениях I, II 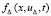 удовлетворяет условию Липшица относительно uΔ. В условиях (30) выполнено
удовлетворяет условию Липшица относительно uΔ. В условиях (30) выполнено 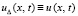 ,
, 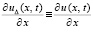 ,
, 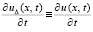 . В Gij решение задачи (30) представимо в виде
. В Gij решение задачи (30) представимо в виде
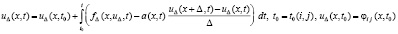 , (31)
, (31)
где 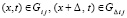 . Приближающий
. Приближающий 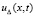 полином будет обозначаться
полином будет обозначаться 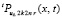 . Полином, приближающий
. Полином, приближающий 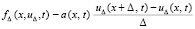 , обозначается
, обозначается 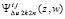 , где z и w из (20). Значения остаточных членов интерполяции изменятся, но их обозначения сохраняются, что не должно приводить к недоразумениям. В этих обозначениях решение (31) приближает последовательность
, где z и w из (20). Значения остаточных членов интерполяции изменятся, но их обозначения сохраняются, что не должно приводить к недоразумениям. В этих обозначениях решение (31) приближает последовательность
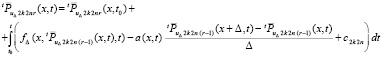 , (32)
, (32)
где 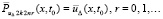 , ввиду неточности начальных данных решение отмечается чертой. Соотношение (31) перейдет в соотношение
, ввиду неточности начальных данных решение отмечается чертой. Соотношение (31) перейдет в соотношение
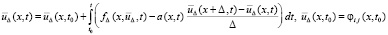 , (33)
, (33)
где 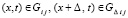 ,
, 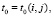
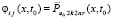 .
.
Всюду ниже значение Δ в (30)–(33) рассматривается как параметр, выбор которого в границах условия (29) позволит оценить сходимость последовательности (28) на основе оценки сходимости последовательности (32).
Из (32), (33)
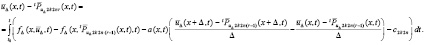
Замечание 1. С учетом постоянного числа подобластей 22k, k = const, не умаляя общности, можно считать, что к 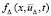 для всех
для всех 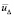 из области
из области 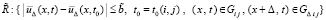 применимо условие Липшица при некотором достаточно большом значении
применимо условие Липшица при некотором достаточно большом значении 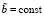 . Последовательность
. Последовательность 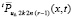 не выводит из
не выводит из 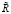 при таком определении
при таком определении 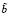 по следующим причинам. При r = 1 полином
по следующим причинам. При r = 1 полином 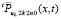 отличается от
отличается от 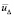 не более, чем на остаточный член однократного интерполирования
не более, чем на остаточный член однократного интерполирования 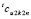 , под интегралом можно применить условие Липшица при этом r:
, под интегралом можно применить условие Липшица при этом r: 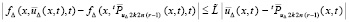 ,
, 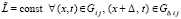 . Тогда
. Тогда 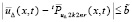 , r = 1, при некотором
, r = 1, при некотором 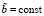 , таком, что
, таком, что 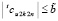 . Дальнейшие рассуждения строятся по индукции. Именно, с повторением данного приема для r ≥ 1 ниже доказывается сходимость
. Дальнейшие рассуждения строятся по индукции. Именно, с повторением данного приема для r ≥ 1 ниже доказывается сходимость 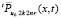 к
к 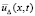 при r → ∞. В частности, полином данной последовательности не будет выводить из
при r → ∞. В частности, полином данной последовательности не будет выводить из 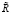
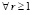 , поэтому к
, поэтому к 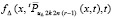 применимо условие Липшица. В качестве константы Липшица
применимо условие Липшица. В качестве константы Липшица 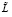 в дальнейшем принят ее максимум по всем подобластям из (1)–(3).
в дальнейшем принят ее максимум по всем подобластям из (1)–(3).
Таким образом, можно предположить, что для некоторого r ≥ 1 выполнено –
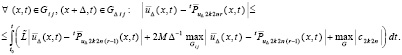 (34)
(34)
В (34) и ниже 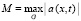 , M = const,
, M = const, 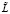 – отмеченное значение константы. Отсюда
– отмеченное значение константы. Отсюда
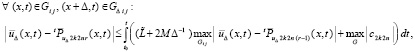
и
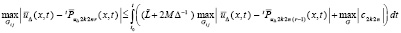 . (35)
. (35)
Сначала рассматривается случай, когда в (35) погрешность однократного интерполирования не превосходит погрешности r – 1 итераций с некоторым постоянным коэффициентом, точнее,
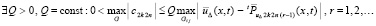 (36)
(36)
В (36) значение Q можно произвольно увеличить, и для 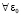 из (29) оно выбирается так, чтобы
из (29) оно выбирается так, чтобы
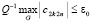 . (37)
. (37)
В дальнейшем исследуется случай, когда (36) нарушается: для некоторого r0 > r окажется выполненным соотношение
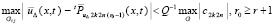 , (38)
, (38)
при этом в силу (38) и (37) нарушение (36) влечет 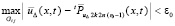 .
.
Пусть сначала (36) не нарушено, в этом случае согласно (35)
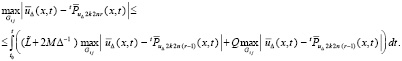 (39)
(39)
Не умаляя общности, можно считать Δ ≤ 1, тогда
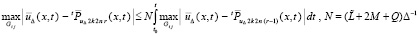 .
.
Если обозначить 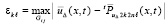 , то неравенство примет вид
, то неравенство примет вид
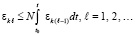 (40)
(40)
где 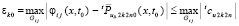 ,
, 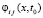 – функция на смежной с Gij границе Gi(j–1),
– функция на смежной с Gij границе Gi(j–1), 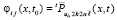 ,
, 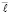 – номер заключительной итерации, выполнявшейся в Gi(j–1). Из (40) и (27)
– номер заключительной итерации, выполнявшейся в Gi(j–1). Из (40) и (27) 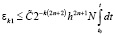 , или,
, или, 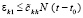 , здесь и ниже
, здесь и ниже 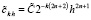 . Тогда
. Тогда 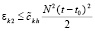 . По индукции
. По индукции 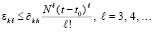 Согласно предположению I, с учетом размеров Gij, верно неравенство
Согласно предположению I, с учетом размеров Gij, верно неравенство 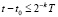 , в результате
, в результате
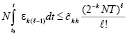 , (41)
, (41)
и
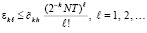 (42)
(42)
В (42) 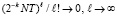 , поэтому
, поэтому 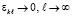 . Отсюда следует, что (36) необходимо окажется нарушенным, –
. Отсюда следует, что (36) необходимо окажется нарушенным, –
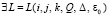 :
: 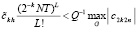 ,
, 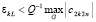 ,
, 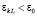 . (43)
. (43)
Пусть (43) и соответственно (38) впервые выполнились при 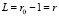 . Для индекса r – 1 еще сохранялось (36), не выполнялось (38) и оставалось верным (39), поэтому при ? = 0
. Для индекса r – 1 еще сохранялось (36), не выполнялось (38) и оставалось верным (39), поэтому при ? = 0
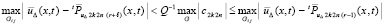 (44)
(44)
и
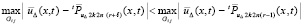 . (45)
. (45)
Если предположить, что (44), (45) выполняются для некоторого ? ≥ 0, то для оценки погрешности (r + ? + 1)-й итерации можно воспользоваться соотношением (35) при соответственных индексах:
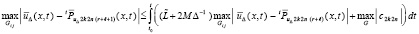 .
.
С учетом (45) и (44)
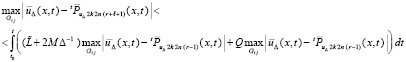 ,
,
или, в прежнем обозначении,
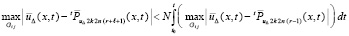 . (46)
. (46)
Согласно (41) правая часть (46) не превосходит 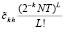 при L = r. С учетом (43)
при L = r. С учетом (43)
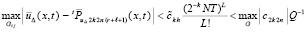 .
.
Отсюда 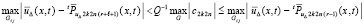 , и соотношения (44), (45) сохраняются при замене ? на ? + 1. В силу индукции и согласно (37)
, и соотношения (44), (45) сохраняются при замене ? на ? + 1. В силу индукции и согласно (37)
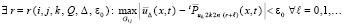 (47)
(47)
Из изложенного вытекает
Лемма 2. Пусть в (1)–(3) зафиксировано 22k подобластей и произвольно выбрана подобласть Gij. При условии, что 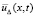 из (33) рассматривается в Gij,
из (33) рассматривается в Gij, 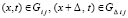 , с теми же начальными условиями на границе с Gi(j–1), с которыми выполняются итерации (32),
, с теми же начальными условиями на границе с Gi(j–1), с которыми выполняются итерации (32), 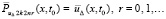 ,
, 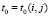 , последовательность (32) равномерно
, последовательность (32) равномерно 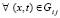 сходится к
сходится к 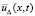 . До тех пор, пока не нарушается соотношение (36), скорость сходимости оценивается из (42). В любом случае имеет место (47).
. До тех пор, пока не нарушается соотношение (36), скорость сходимости оценивается из (42). В любом случае имеет место (47).
Попутно показано, что последовательность 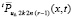 не выводит из области
не выводит из области 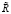 , как и предполагалось в замечании 1.
, как и предполагалось в замечании 1.
Рассматриваемое приближение непрерывно, следовательно, равномерно непрерывно в замкнутой подобласти Gij. Поскольку для (33) и для (32) в Gij выполнено 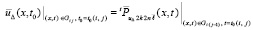 , где
, где 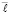 – номер заключительной итерации, выполнявшейся в Gi(j–1), то непрерывность и равномерная непрерывность приближения (32) сохраняется при переходе от Gi(j–1) к Gij и, таким образом, во всем временном слое
– номер заключительной итерации, выполнявшейся в Gi(j–1), то непрерывность и равномерная непрерывность приближения (32) сохраняется при переходе от Gi(j–1) к Gij и, таким образом, во всем временном слое 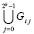 для каждого i = const.
для каждого i = const.
Отсюда вытекает
Следствие 1. Кусочно-интерполяционное приближение решения задачи (30) с итерационным уточнением в каждой подобласти Gij при любом количестве итераций является равномерно-непрерывной функцией. В частности, при k = 0 приближение равномерно-непрерывно в G, при k > 0 оно кусочно-непрерывно в G и сохраняет равномерную непрерывность в слое подобластей 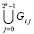 для каждого i = const.
для каждого i = const.
Для 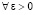 (47) сохранится, если взять
(47) сохранится, если взять 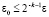 , априори в (29) взять соответственное значение Δ и в (47) указать зависящее от них r:
, априори в (29) взять соответственное значение Δ и в (47) указать зависящее от них r:
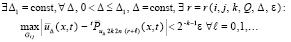 (48)
(48)
Из того, что на выходе из Gij полином 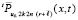 задает начальные условия
задает начальные условия 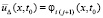 ,
, 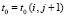 , в Gi(j+1) , и при этом выполняется (48), вытекает оценка изменения начальных условий при переходе от одной подобласти к другой.
, в Gi(j+1) , и при этом выполняется (48), вытекает оценка изменения начальных условий при переходе от одной подобласти к другой.
Следствие 2. В условиях леммы 2 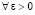 найдется
найдется 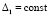 , такое что
, такое что 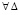 из (29),
из (29), 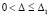 , максимальное отклонение последовательности (32) в Gij от
, максимальное отклонение последовательности (32) в Gij от 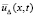 оценивается из (48). Этого же значения не превысит максимальное отклонение начальных условий в Gi(j+1) от тех начальных условий
оценивается из (48). Этого же значения не превысит максимальное отклонение начальных условий в Gi(j+1) от тех начальных условий 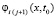 , которые задавались бы при переходе из Gij в Gi(j+1) точным решением, взятым с начальными условиями из Gij в виде
, которые задавались бы при переходе из Gij в Gi(j+1) точным решением, взятым с начальными условиями из Gij в виде 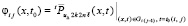 .
.
Устойчивость решения задачи (30) сохраняется в каждой подобласти и означает, что 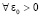
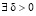 , такое, что если
, такое, что если 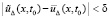 ,
, 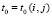 , то
, то 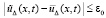
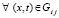 . В качестве невозмущенного решения в Gij рассматривается
. В качестве невозмущенного решения в Gij рассматривается 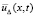 . Его возмущение – точное (не получающееся вследствие приближения) решение в этой подобласти
. Его возмущение – точное (не получающееся вследствие приближения) решение в этой подобласти 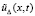 , соответственное возмущенным начальным условиям
, соответственное возмущенным начальным условиям 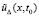 . По следствию 2 максимальное отклонение начальных данных при переходе от Gij к Gi(j+1) оценивается из (48). Аналогично, при переходе от Gi(j–1) к Gij, где это достигается за счет выбора Δ и r в Gi(j–1). Отсюда для
. По следствию 2 максимальное отклонение начальных данных при переходе от Gij к Gi(j+1) оценивается из (48). Аналогично, при переходе от Gi(j–1) к Gij, где это достигается за счет выбора Δ и r в Gi(j–1). Отсюда для 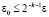 найдется δ > 0, и такие Δ, r для последовательности (32) в Gi(j–1), что выполняются соотношения:
найдется δ > 0, и такие Δ, r для последовательности (32) в Gi(j–1), что выполняются соотношения:
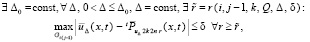 (49)
(49)
и
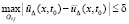 ,
, 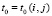 ,
,
поэтому, в силу устойчивости,
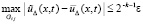 . (50)
. (50)
Пусть 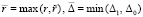 , где r и Δ1 из (48),
, где r и Δ1 из (48), 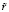 и Δ0 из (49) . Из (48) и (50)
и Δ0 из (49) . Из (48) и (50)
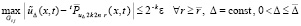 . (51)
. (51)
Поскольку число подобластей 22k зафиксировано, можно выбрать наименьшее по всем i, j значение 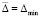 , и, при этом значении
, и, при этом значении 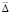 , наибольший по всем i, j номер rmax, которые обеспечат выполнение (48), следствия 2, соотношений (49), а также (50), (51) одновременно во всех подобластях Gij:
, наибольший по всем i, j номер rmax, которые обеспечат выполнение (48), следствия 2, соотношений (49), а также (50), (51) одновременно во всех подобластях Gij:
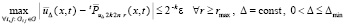 , (52)
, (52)
где 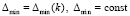 ,
, 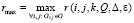 . Суммой отклонений во всех подобластях слоя
. Суммой отклонений во всех подобластях слоя 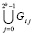 , i = const, можно оценить максимальное отклонение кусочно-интерполяционного приближения с итерационным уточнением от точного невозмущенного решения задачи (30) во всем этом слое:
, i = const, можно оценить максимальное отклонение кусочно-интерполяционного приближения с итерационным уточнением от точного невозмущенного решения задачи (30) во всем этом слое:
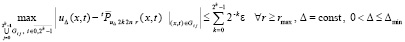 ,
,
или
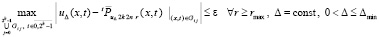 .
.
Согласно выбору максимума в (52), использованному в этих оценках, они сохраняются для любого слоя  с постоянным
с постоянным  из области G. Отсюда, а также из того, что по построению вспомогательной задачи (30) при любом Δ из (29)
из области G. Отсюда, а также из того, что по построению вспомогательной задачи (30) при любом Δ из (29) 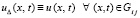 , где u(x, t) – решение уравнения (23), вытекает
, где u(x, t) – решение уравнения (23), вытекает
Лемма 3. В условиях леммы 2 кусочно-интерполяционное приближение с итерационным уточнением (32) решения задачи (30) равномерно сходится в области G к решению u(x, t) задачи (23). При этом
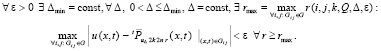 (53)
(53)
Относительно равномерной и кусочной непрерывности последовательных приближений без изменений повторяется утверждение следствия 1, с той оговоркой, что оно относится не только к решению задачи (30), но также и к решению задачи (23).
Замечание 2. Условия и утверждение леммы 3 сохранятся без существенных изменений, если кусочно-интерполяционное приближение решения задачи (30) с итерационным уточнением применить к решению задачи
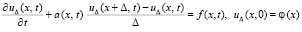 , (54)
, (54)
в виде
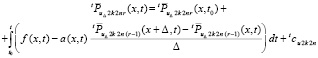 . (55)
. (55)
Аналогично предыдущему, доказывается сходимость (55) к решению uΔ(x, t) задачи (54), а также приближение этого решения с точностью до 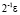 . Из того, что
. Из того, что 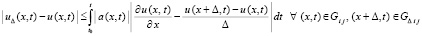 , где u(x, t) – решение задачи (23), с учетом (29), следует
, где u(x, t) – решение задачи (23), с учетом (29), следует 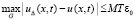 . При выборе
. При выборе 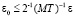 получится
получится 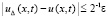 . В результате (55) будет приближать u(x, t) с точностью до ε.
. В результате (55) будет приближать u(x, t) с точностью до ε.
Тем не менее сходимость (32) к решению задачи (30) означает сходимость непосредственно к решению задачи (23), что используется ниже.
Сходимость основной последовательности к решению линейного уравнения переноса
Для перехода от (32) к (28), в условиях леммы 3 и с учетом (53), предварительно оценивается разность
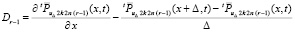 . (56)
. (56)
С применением теоремы о среднем,
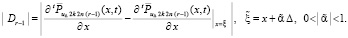 (57)
(57)
Повторное применение теоремы влечет
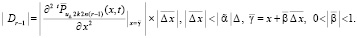 (58)
(58)
По построению, 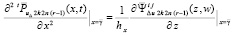 , где z, w из (20), отсюда
, где z, w из (20), отсюда
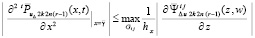 . (59)
. (59)
Правая часть (59) ограничена в силу следующих причин. Последовательность (32) сходится к решению u(x, t) задачи (23), и выполнено (53). Функция u(x, t) ограничена в G (в GΔ), в частности в Gij, поэтому при  значения
значения  также ограничены в Gij. Поскольку
также ограничены в Gij. Поскольку 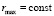 , то и вся последовательность
, то и вся последовательность 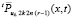 ограничена в Gij
ограничена в Gij 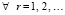 В G, GΔ и Gij ограничена функция
В G, GΔ и Gij ограничена функция 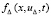 . Как следствие, при замене
. Как следствие, при замене 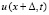 , u(x, t) в выражении
, u(x, t) в выражении 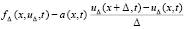 из (30) на полиномы
из (30) на полиномы 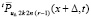 ,
, 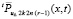 последовательность данных выражений останется ограниченной в Gij. Элементы именно этой последовательности интерполируются полиномами
последовательность данных выражений останется ограниченной в Gij. Элементы именно этой последовательности интерполируются полиномами 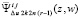 :
:
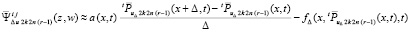 .
.
В процессе итерационного уточнения полином 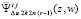 не меняет степень и расстояние между узлами, при этом множество всех узловых значений оказывается ограниченным в продолжение всего итерационного процесса. Структура полинома аналогична (7), таким образом, ограничены его коэффициенты. В то же время коэффициенты стоят перед не меняющимися частями полинома, которые непрерывны в Gij. Отсюда полином
не меняет степень и расстояние между узлами, при этом множество всех узловых значений оказывается ограниченным в продолжение всего итерационного процесса. Структура полинома аналогична (7), таким образом, ограничены его коэффициенты. В то же время коэффициенты стоят перед не меняющимися частями полинома, которые непрерывны в Gij. Отсюда полином 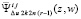 ограничен в Gij. Взятие производной от полинома с рассматриваемыми свойствами сохраняет ограниченность коэффициентов и непрерывность выражения полинома, представляющего производную. В результате
ограничен в Gij. Взятие производной от полинома с рассматриваемыми свойствами сохраняет ограниченность коэффициентов и непрерывность выражения полинома, представляющего производную. В результате 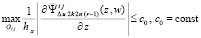 . С учетом
. С учетом 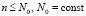 , и k = const,
, и k = const, 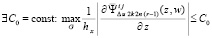 . Подстановка C0 в (59), затем в (58), с учетом (57) влечет
. Подстановка C0 в (59), затем в (58), с учетом (57) влечет 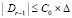 . Отсюда
. Отсюда 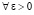 при априорном выборе
при априорном выборе 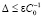 будет выполнено
будет выполнено
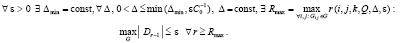 (60)
(60)
Пусть наряду с (32) рассматривается последовательность
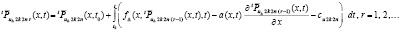 (61)
(61)
Из (33) и (61), при равенстве начальных условий в Gij,
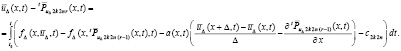 (62)
(62)
В обозначении 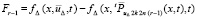 (62) эквивалентно
(62) эквивалентно
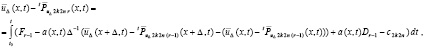
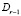 из (56). Применение условия Липшица к
из (56). Применение условия Липшица к 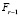 влечет
влечет
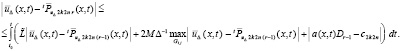 (63)
(63)
Пусть 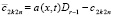 . Согласно (60)
. Согласно (60) 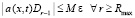 . Если априори выбрать
. Если априори выбрать 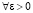 так, чтобы
так, чтобы 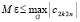 , то при
, то при 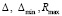 из (60), взятых для данного ε,
из (60), взятых для данного ε,
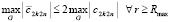 . (64)
. (64)
В предположении 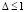 из (63) следует
из (63) следует 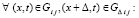
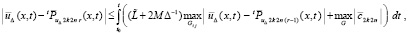
и
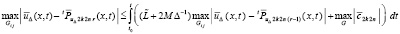 . (65)
. (65)
Для (65) с точностью до обозначений и постоянных множителей воспроизводятся все рассуждения, преобразования и соотношения от (35) до (53) включительно. С такой оговоркой рассматриваемые преобразования инвариантны относительно Δ, выбранного в (60) и, соответственно, в (64). В (64) предполагалось 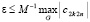 ,
, 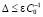 , или,
, или, 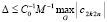 . С этим ограничением получится, –
. С этим ограничением получится, –
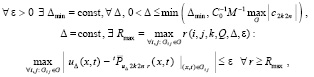 (66)
(66)
где 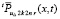 из (61),
из (61), 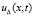 – решение задачи (30). Поскольку
– решение задачи (30). Поскольку 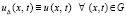 , последовательность (61) с оценкой (66) приближает решение задачи (23). По сравнению с (40)–(53) изменится коэффициент в аналоге (40). Именно, при выполнении оценки εk0 с учетом (64) получится
, последовательность (61) с оценкой (66) приближает решение задачи (23). По сравнению с (40)–(53) изменится коэффициент в аналоге (40). Именно, при выполнении оценки εk0 с учетом (64) получится 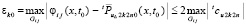 . Соответственно,
. Соответственно, 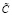 потребуется заменить на
потребуется заменить на 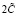 . Если обозначить
. Если обозначить 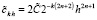 , то вид дальнейших оценок сохранится. Таким образом, имеет место
, то вид дальнейших оценок сохранится. Таким образом, имеет место
Лемма 4. В условиях леммы 2 кусочно-интерполяционное приближение с итерационным уточнением вида (61) решения задачи (30) равномерно сходится в области G к решению u(x, t) задачи (23). При этом 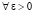 выполняется соотношение (66), где
выполняется соотношение (66), где 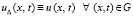 . Относительно равномерной и кусочной непрерывности последовательных приближений (61) без изменений повторяется утверждение леммы 3.
. Относительно равномерной и кусочной непрерывности последовательных приближений (61) без изменений повторяется утверждение леммы 3.
В (61), в силу леммы 4, для Δ из (66) 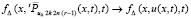 , r → ∞, и
, r → ∞, и
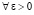
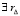 :
: 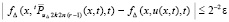
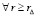 . (67)
. (67)
С другой стороны, из (23), (30) и (29) следует
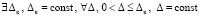 :
: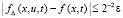 . (68)
. (68)
Пусть рассматривается аналог последовательности (61), получаемый заменой в (61) 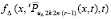 на
на 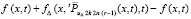 , при этом разность
, при этом разность 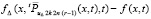 присоединяется к остаточному члену
присоединяется к остаточному члену 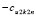 и в сумме образует новый остаточный член
и в сумме образует новый остаточный член 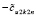 . Из (67), (68)
. Из (67), (68) 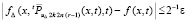 при условии
при условии 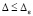 и
и 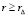 . В предположении
. В предположении 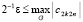 , получится
, получится 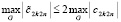 . В результате,
. В результате,
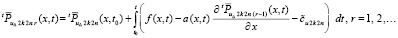 , (69)
, (69)
где
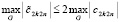 ,
, 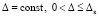 ,
, 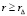 . (70)
. (70)
Из (33) и (69), при условии равенства начальных условий в Gij,
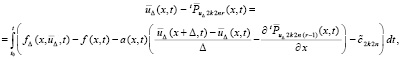
или
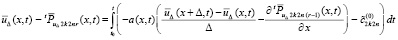 , (71)
, (71)
где 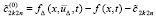 – новый остаточный член. При этом согласно (70) и (68), с учетом предположения
– новый остаточный член. При этом согласно (70) и (68), с учетом предположения 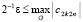 ,
,
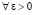 ,
, 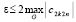 ,
, 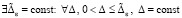 ,
, 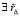 :
:
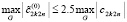
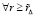 . (72)
. (72)
Тождественное преобразование (71) с учетом (56) влечет
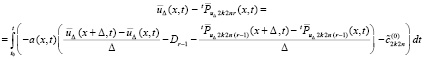
или
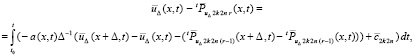
где 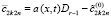 . Ввиду
. Ввиду 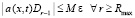 , в предположении
, в предположении 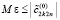 , будет выполняться
, будет выполняться 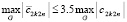 . Аналогично предыдущему, предположение относительно ε повлечет изменение ограничений Δ и r. Именно, с учетом (72),
. Аналогично предыдущему, предположение относительно ε повлечет изменение ограничений Δ и r. Именно, с учетом (72),
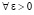 ,
, 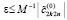 ,
,
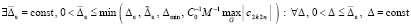 ,
,
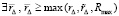 , такие, что
, такие, что 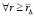 выполняется
выполняется
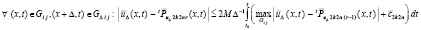 ,
,
и, в тех же условиях,
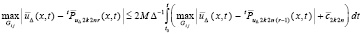 .
.
Остается повторить проделанные ранее рассуждения, чтобы с точностью до обозначений, значений констант и постоянных множителей вывести аналог соотношения (66), в котором 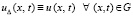 из (23),
из (23), 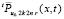 из (69) с точностью до обозначения совпадает с
из (69) с точностью до обозначения совпадает с 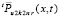 из (28). Отсюда рассуждения, проделанные с данными видоизменениями для
из (28). Отсюда рассуждения, проделанные с данными видоизменениями для 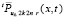 из (69) и
из (69) и 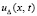 из (30), сохраняются для
из (30), сохраняются для 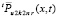 из (28) и u(x, t) из (23). Сохраняются также описанные выше ограничения значений констант. Однако они дополнительно скорректируются при введении аналога соотношений (36), (37) путем выбора Q для нового остаточного члена
из (28) и u(x, t) из (23). Сохраняются также описанные выше ограничения значений констант. Однако они дополнительно скорректируются при введении аналога соотношений (36), (37) путем выбора Q для нового остаточного члена 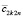 . Чтобы не усложнять обозначений, ниже данные ограничения неявно подразумеваются, но не детализируются. С этой оговоркой, в условиях леммы 2, выполняется соотношение
. Чтобы не усложнять обозначений, ниже данные ограничения неявно подразумеваются, но не детализируются. С этой оговоркой, в условиях леммы 2, выполняется соотношение
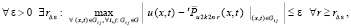 (73)
(73)
где u(x, t) – решение уравнения (23), 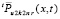 из (28); по построению
из (28); по построению 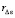 зависит от ε, Δ и
зависит от ε, Δ и 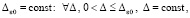 Δ из (29);
Δ из (29); 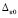 существует в качестве параметра условий сходимости (69), на основе которых доказывается сходимость (28).
существует в качестве параметра условий сходимости (69), на основе которых доказывается сходимость (28).
Имеет место
Теорема 2. Пусть в области G из (1)–(3) зафиксировано 22k подобластей. Пусть в каждой подобласти Gij уравнение (24) рассматривается с теми же начальными условиями на границе с Gi(j–1), с которыми выполняются итерации (28), при этом они сохраняются с изменением номера итерации: 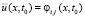 ,
, 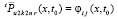 ,
, 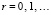 ,
, 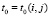 . Тогда кусочно-интерполяционное приближение с итерационным уточнением (28) решения задачи (23) равномерно сходится в G к решению u(x, t) с оценкой (73). Относительно равномерной и кусочной непрерывности последовательных приближений (28) без принципиальных изменений формулируется аналог утверждения леммы 4, данного относительно приближений (61).
. Тогда кусочно-интерполяционное приближение с итерационным уточнением (28) решения задачи (23) равномерно сходится в G к решению u(x, t) с оценкой (73). Относительно равномерной и кусочной непрерывности последовательных приближений (28) без принципиальных изменений формулируется аналог утверждения леммы 4, данного относительно приближений (61).
Приближение частных производных
Пусть выполнены условия леммы 2 и теоремы 2. Тогда
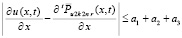 ,
,
где
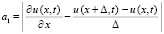 ,
,
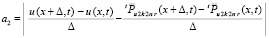 ,
,
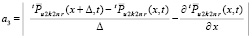 .
.
Слагаемое a1 оценивается из (29), для оценки a3 можно повторить рассуждения, проделанные для (56)–(60). При этом Δ = const можно считать столь малым, что 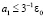 и
и 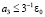 . Кроме того,
. Кроме того, 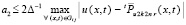 . В (73) для такого Δ ничто не исключает
. В (73) для такого Δ ничто не исключает 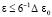 , при необходимости можно указать соответственные Δε и
, при необходимости можно указать соответственные Δε и 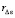 . Тогда
. Тогда 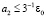 . В неравенствах можно перейти к максимуму по
. В неравенствах можно перейти к максимуму по 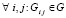 . В результате
. В результате
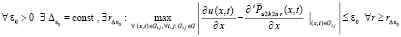 . (74)
. (74)
Производная 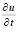 приближается с оценкой, зависящей от размера подобласти. Из (23) и (69)
приближается с оценкой, зависящей от размера подобласти. Из (23) и (69) 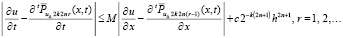 , где учитывается (70) и c = 2C. С подстановкой (74),
, где учитывается (70) и c = 2C. С подстановкой (74), 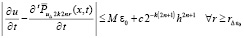 . Здесь и в (74) вместо ε0 можно взять
. Здесь и в (74) вместо ε0 можно взять 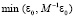 , соответственно скорректировав
, соответственно скорректировав 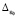 и
и 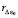 . Тогда
. Тогда
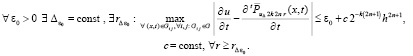
Случай квазилинейного уравнения переноса
Пусть рассматривается задача
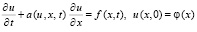 , (75)
, (75)
где принимается, что f(x, t) – заданная функция в области 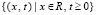 , φ(x) – заданная функция
, φ(x) – заданная функция 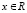 , a(u, x, t) – функция, заданная в области
, a(u, x, t) – функция, заданная в области 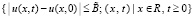 ,
, 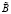 – некоторая постоянная, выбор которой оговаривается аналогично условию I. Изложенный выше метод рассматривается в предположениях I–III, с тем изменением, что a(u, x, t) задана в области
– некоторая постоянная, выбор которой оговаривается аналогично условию I. Изложенный выше метод рассматривается в предположениях I–III, с тем изменением, что a(u, x, t) задана в области 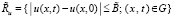 , и относительно (75) приняты все предположения, сделанные относительно (23). Из (75)
, и относительно (75) приняты все предположения, сделанные относительно (23). Из (75)
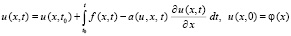 .
.
Аналогично предыдущему, определяются последовательности
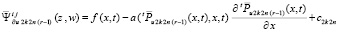 ,
,
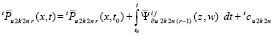 ,
,
где z, w из (20). Отсюда,
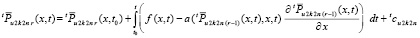 .
.
Рассматривается вспомогательная задача
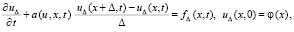 (76)
(76)
где
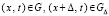 ,
, 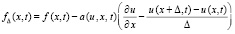 ,
, 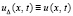 из (75)
из (75) 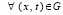 ,
, 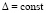 произвольно выбрано в соответствии с (29). В Gij при
произвольно выбрано в соответствии с (29). В Gij при 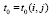 (75) преобразуется к виду
(75) преобразуется к виду
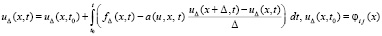 , (77)
, (77)
где 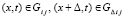 . Строится последовательность
. Строится последовательность
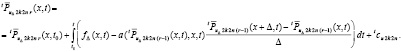 (78)
(78)
Пусть в (77) и (78) начальные условия одинаковы: 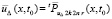 ,
, 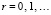 ,
, 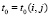 , решение
, решение 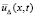 отмечается чертой. Тогда
отмечается чертой. Тогда
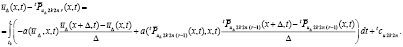 (79)
(79)
Выражение под знаком интеграла преобразуется в сумму 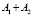 , где
, где
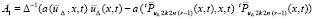 ,
,
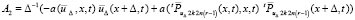 .
.
В A1 можно добавить и вычесть 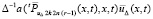 . Отсюда
. Отсюда
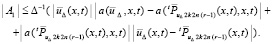
Учитывая аналог замечания 1, можно применить условие Липшица к функции 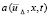 :
:
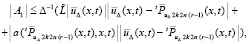
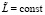 .
.
В результате 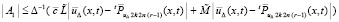 , где
, где 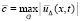 ,
, 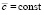 ,
, 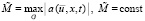 . Отсюда
. Отсюда
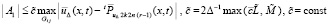 .
.
В A2 можно добавить и вычесть 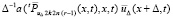 . Тогда
. Тогда
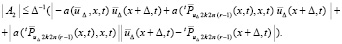
С применением условия Липшица,
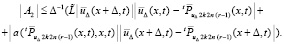
Как и выше, 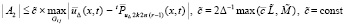 . Отсюда и из (79)
. Отсюда и из (79) 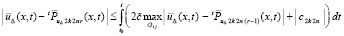 . Ввиду произвольности
. Ввиду произвольности 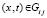 ,
,
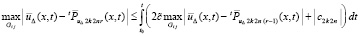 . (80)
. (80)
На основе (80) можно рассматривать преобразования, аналогичные выполненным для линейного уравнения, включая (36), (40), а также переход от (30) к (23), в данном случае – от (76) к (75).
Если в (75) вместо f(x, t) рассматривать f(u, x, t), то в (79) в качестве слагаемого под знаком интеграла появится разность 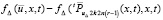 , модуль которой оценивается по условию Липшица. Это изменит значение константы в (80), но не исключает оценку сходимости метода.
, модуль которой оценивается по условию Липшица. Это изменит значение константы в (80), но не исключает оценку сходимости метода.
Численный эксперимент
Изложенный метод реализован программно, код программы дан в [6]. Реализация содержит отклонения от исходного описания. Именно, не использован переход к описанному треугольнику области G. Интерполирование выполняется на основе (7) с переводом в форму (9) без удвоения степени полинома. Аналог (28) 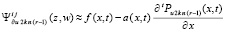 ,
, 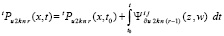 , служит для итерационного уточнения, коэффициенты преобразуются с учетом (20)–(22). Интерполяция с итерационным уточнением выполняется в G, кроме того, в области, получающейся сдвигом G вдоль OX влево (Gleft) на половину длины катета треугольника, образованного узлами интерполяции. Этот же процесс выполняется в области, полученной аналогичным сдвигом G вправо (Gright). Для приближения решения в G выбираются полиномы из третьей слева направо четверти области Gleft (ниже они обозначаются
, служит для итерационного уточнения, коэффициенты преобразуются с учетом (20)–(22). Интерполяция с итерационным уточнением выполняется в G, кроме того, в области, получающейся сдвигом G вдоль OX влево (Gleft) на половину длины катета треугольника, образованного узлами интерполяции. Этот же процесс выполняется в области, полученной аналогичным сдвигом G вправо (Gright). Для приближения решения в G выбираются полиномы из третьей слева направо четверти области Gleft (ниже они обозначаются 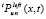 ) и первой слева направо четверти области Gright (ниже
) и первой слева направо четверти области Gright (ниже 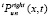 ), а также из промежуточной между ними половины области G (ниже
), а также из промежуточной между ними половины области G (ниже 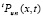 ). Этим исключаются наименее точные приближения вдоль сторон треугольника, образованного узлами интерполяции. Полный процесс приближения со сдвигами вдоль оси OX циклически повторяется со сдвигом по вертикали вдоль оси OT. Окончательные полиномиальные приближения выбираются из десятой части, отсчитанной от нижнего основания вертикально сдвигаемой прямоугольной области («нижний прямоугольный слой»), что устойчиво повышает точность приближения. В процессе смещения вдоль OT полученные на верхней границе текущего нижнего прямоугольного слоя приближения решения принимаются за начальные условия для следующего за ним временного слоя. Контроль точности привязан к текущему нижнему прямоугольному слою. Степень полинома выбирается на основе минимизации аналога невязки (ниже просто невязки) специального вида. Невязка
). Этим исключаются наименее точные приближения вдоль сторон треугольника, образованного узлами интерполяции. Полный процесс приближения со сдвигами вдоль оси OX циклически повторяется со сдвигом по вертикали вдоль оси OT. Окончательные полиномиальные приближения выбираются из десятой части, отсчитанной от нижнего основания вертикально сдвигаемой прямоугольной области («нижний прямоугольный слой»), что устойчиво повышает точность приближения. В процессе смещения вдоль OT полученные на верхней границе текущего нижнего прямоугольного слоя приближения решения принимаются за начальные условия для следующего за ним временного слоя. Контроль точности привязан к текущему нижнему прямоугольному слою. Степень полинома выбирается на основе минимизации аналога невязки (ниже просто невязки) специального вида. Невязка
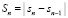
определяется из соотношений
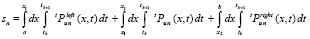 ,
,
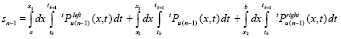 ,
,
и вычисляется в текущем (k-м) нижнем прямоугольном слое. Здесь xi – соответственные границы сдвигов вдоль OX, tk, 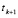 – временные границы k-го нижнего прямоугольного слоя. Геометрически невязка представляет разность объемов параллелепипедов, ограниченных криволинейными поверхностями, которые задаются кусочно-интерполяционными приближениями решения u(x, t) посредством полиномов степени n и n – 1 соответственно. Сходная форма невязки используется при выборе числа итераций r, для каждой разновидности полиномов
– временные границы k-го нижнего прямоугольного слоя. Геометрически невязка представляет разность объемов параллелепипедов, ограниченных криволинейными поверхностями, которые задаются кусочно-интерполяционными приближениями решения u(x, t) посредством полиномов степени n и n – 1 соответственно. Сходная форма невязки используется при выборе числа итераций r, для каждой разновидности полиномов 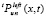 ,
, 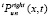 и
и 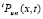 это число выбирается отдельно. Для
это число выбирается отдельно. Для 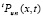 вычисляется
вычисляется 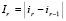 ,
, 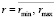 , где
, где 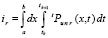 ,
, 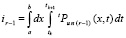 . Аналогичные вычисления выполняются для
. Аналогичные вычисления выполняются для 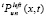 и
и 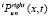 . Фиксируются значения n и r, при которых Sn и Ir принимают наименьшие значения.
. Фиксируются значения n и r, при которых Sn и Ir принимают наименьшие значения.
Эксперимент составляют примеры задач, имеющих точные решения, сравнением с ними определяется погрешность приближенных решений.
Пример 1. Задача Коши
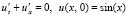 , (81)
, (81)
точное решение 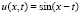 , рассматривается как модель для сравнения численных методов [10]. Ее приближенное решение ниже дано в
, рассматривается как модель для сравнения численных методов [10]. Ее приближенное решение ниже дано в 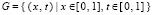 . В табл. 1 приводятся значения абсолютной погрешности кусочно-интерполяционного решения с итерационным уточнением (здесь и ниже – реализация в Delphi, тип данных extended) в 10 равномерно распределенных точках на отрезке
. В табл. 1 приводятся значения абсолютной погрешности кусочно-интерполяционного решения с итерационным уточнением (здесь и ниже – реализация в Delphi, тип данных extended) в 10 равномерно распределенных точках на отрезке 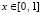 при значениях t = 0,1 и t = 1,0 (степень интерполяционного полинома n = 13, число итераций – r = 50, область G не делится на подобласти). В первом столбце таблицы – время решения на персональном компьютере (для сравниваемых методов время на том же компьютере дано в табл. 3, 4).
при значениях t = 0,1 и t = 1,0 (степень интерполяционного полинома n = 13, число итераций – r = 50, область G не делится на подобласти). В первом столбце таблицы – время решения на персональном компьютере (для сравниваемых методов время на том же компьютере дано в табл. 3, 4).
Таблица 1
Абсолютная погрешность приближенного решения задачи (81)
|
11 s |
hx ≈ 0.08 |
ht ≈ 0.04 |
t = 0.1 |
|
|
|
… |
|
|
|
t = 1.0 |
|
|
|
… |
|
|
Пример 2. Задача Коши
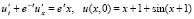 (82)
(82)
имеет решение 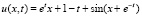 . Приближенное решение построено в квадрате G из примера 1. Табл. 2 содержит абсолютную погрешность предложенного метода в точках, распределенных как в примере 1 (n = 13, r = 25,число подобластей Gij равно 4).
. Приближенное решение построено в квадрате G из примера 1. Табл. 2 содержит абсолютную погрешность предложенного метода в точках, распределенных как в примере 1 (n = 13, r = 25,число подобластей Gij равно 4).
Таблица 2
Абсолютная погрешность приближенного решения задачи (82)
|
23 s |
hx ≈ 0.04 |
ht ≈ 0.02 |
t = 0.1 |
5.4×10-19 |
0.0 |
2.2×10-19 |
… |
4.3×10-19 |
0.0 |
|
t = 1.0 |
1.8×10-18 |
3.3×10-19 |
9.8×10-19 |
… |
6.5×10-19 |
5.6×10-18 |
В системах компьютерной математики решение рассматриваемых уравнений опирается на граничные условия. Для единства условий сравнения ниже даны решения начально-краевых задач в системах MathCAD, Maрle и предложенным методом без его принципиальных изменений. В табл. 3, 4 строка (1) соответствует предложенному методу, (2) – функции pdesolve программы MathCAD (выбор разностного метода отвечает наилучшему приближению), (3) – pdsolve программы Maрle. Соотношение шагов удовлетворяет условию сходимости метода сеток для уравнений гиперболического типа.
Пример 3. Рассматривается начально-краевая задача
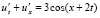 ,
, 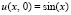 ,
, 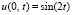 . (83)
. (83)
Погрешность ее решения в области из примера 1 сравнивается в 10 равномерно распределенных точках на отрезке 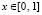 при значении t = 1. В предложенном методе n = 13, r = 20, область G не делится на подобласти.
при значении t = 1. В предложенном методе n = 13, r = 20, область G не делится на подобласти.
Таблица 3
Абсолютная погрешность приближенного решения задачи (83)
|
(1) |
4 s |
|
|
|
|
|
… |
|
|
|
(2) |
14 s |
|
|
|
|
|
… |
|
|
|
(3) |
4 min 27 s |
|
|
|
|
|
… |
|
|
Пример 4. В [11] рассматривается нелинейная краевая задача
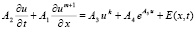 ,
, 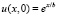 ,
, 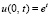 . (84)
. (84)
Если решение взято в виде 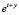 ,
, 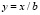 , то источник E принимает вид
, то источник E принимает вид
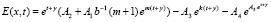 .
.
В качестве опорных согласно [11] взяты значения: m = 0, 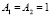 ,
, 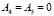 и b = 1. В табл. 4 приводится погрешность приближенного решения при различных значениях параметров k и A3 (первая строка таблицы) в 10 равномерно распределенных точках из примера 3. Остальные обозначения соответствуют табл. 3. В предложенном методе n = 13, r = 20, r = 35, r = 40 соответственно параметрам данных задач, деление G на подобласти не выполнялось.
и b = 1. В табл. 4 приводится погрешность приближенного решения при различных значениях параметров k и A3 (первая строка таблицы) в 10 равномерно распределенных точках из примера 3. Остальные обозначения соответствуют табл. 3. В предложенном методе n = 13, r = 20, r = 35, r = 40 соответственно параметрам данных задач, деление G на подобласти не выполнялось.
Таблица 4
Абсолютная погрешность приближенного решения задачи (84)
|
k = 1, A3 = 0 |
|||||||||
|
(1) |
4 s |
|
|
|
|
|
… |
|
|
|
(2) |
24 s |
|
|
|
|
|
… |
|
|
|
(3) |
4 min 37 s |
|
|
|
|
|
… |
|
|
|
k = 1, A3 = –1 |
|||||||||
|
(1) |
10 s |
|
|
|
|
|
… |
|
|
|
(2) |
25 s |
|
|
|
|
|
… |
|
|
|
(3) |
4 min 44 s |
|
|
|
|
|
… |
|
|
|
k = 2, A3 = –1 |
|||||||||
|
(1) |
16 s |
|
|
|
|
|
… |
|
|
|
(2) |
1 min 47 s |
|
|
|
|
|
… |
|
|
|
(3) |
51 min 14 s |
|
|
|
|
|
… |
|
|
В [11] приводится относительная погрешность 2,21 % при t = 1. Предложенный метод в этом случае дает 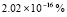 .
.
Пример 5. Рассматривается задача Коши
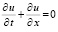 ,
,
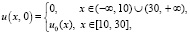
где 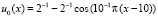 . Точное решение имеет вид [2]:
. Точное решение имеет вид [2]:
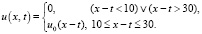
Область приближения
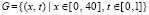 .
.
В точке с абсциссой x = 21, соответствующей пику волны при t = 1, абсолютная погрешность рекурсивной 5-точечной разностной схемы MathCAD составляет 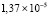 , предложенный метод в этой точке даст
, предложенный метод в этой точке даст 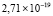 . Кусочная непрерывность приближения позволяет сравнительно адекватно отразить характер изменения решения в окрестности амплитуды. В начале и в конце волны погрешность можно снизить, окружив эти точки узкой областью с большим количеством подобластей. Так, в точке x = 11,2, соответствующей окрестности начала волны при t = 1, абсолютная погрешность составит
. Кусочная непрерывность приближения позволяет сравнительно адекватно отразить характер изменения решения в окрестности амплитуды. В начале и в конце волны погрешность можно снизить, окружив эти точки узкой областью с большим количеством подобластей. Так, в точке x = 11,2, соответствующей окрестности начала волны при t = 1, абсолютная погрешность составит 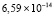 .
.
В аналогичных исследованиях точность данных численных экспериментов, как правило, не превосходят точность в строках 2, 3 табл. 3, 4. Так, в [12] строится решение гиперболического уравнения второго порядка с помощью полиномов Тейлора от двух переменных. Абсолютная погрешность этого метода в квадрате из примера 1 при t = 0 составляет 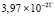 , но с ростом t растет до
, но с ростом t растет до 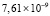 . В [13] эта же задача решается на основе кубической тригонометрической сплайн-интерполяции. В
. В [13] эта же задача решается на основе кубической тригонометрической сплайн-интерполяции. В 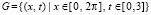 абсолютная погрешность приближения не ниже
абсолютная погрешность приближения не ниже 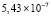 . В [14] строится кусочно-интерполяционное решение уравнения переноса с помощью кубической B-сплайн квазиинтерполяции, ее абсолютная погрешность в квадрате из примера 1 не ниже
. В [14] строится кусочно-интерполяционное решение уравнения переноса с помощью кубической B-сплайн квазиинтерполяции, ее абсолютная погрешность в квадрате из примера 1 не ниже 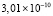 при t = 1.
при t = 1.
Сравнительная точность предложенного метода достигается за счет итерационного уточнения (не применяемого в работах, с которыми проводилось сравнение). Его реализация опирается на аналитический вид первообразной и производной от интерполяционного полинома, преобразованного в форму алгебраического полинома с числовыми коэффициентами. Для снижения погрешности существенны также сдвиги области приближения по горизонтали и вертикали, с их помощью обходится зона погрешности экстраполяции за пределами треугольного расположения узлов интерполяционного полинома.
Замечание 3. В табл. 1–4 время решения задачи предложенным методом дано без использования программного выбора степени полинома и числа итераций. С программным выбором n и r время существенно возрастает, наиболее долго решается задача (82) – 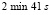 . В целом с таким выбором время решения занимает промежуточное значение между MathCAD и Maрle в границах погрешности, приведенной в таблицах.
. В целом с таким выбором время решения занимает промежуточное значение между MathCAD и Maрle в границах погрешности, приведенной в таблицах.
Алгоритм выбора параметров можно выполнить параллельно по всем сравниваемым значениям невязки Sn одновременно для всех степеней полиномов n (в силу взаимной независимости сравниваемых значений), аналогично, по всем Ir для всех значений r. По параллельно найденным значениям без труда определяются параметры минимизации погрешности при наименьшей временной сложности. Вместе с тем вычислительный алгоритм решения рассматриваемой задачи Коши является взаимно независимым по временным слоям подобластей 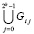 , i = const, поэтому решение распараллеливается по всем номерам слоев
, i = const, поэтому решение распараллеливается по всем номерам слоев 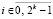 , ускоряя последовательный алгоритм пропорционально 2k. Распараллеливание допускает также алгоритм вычисления коэффициентов и значения интерполяционного полинома Ньютона. Для полинома от одной переменной временная сложность оценивается в [15], для полинома от двух переменных – в [6].
, ускоряя последовательный алгоритм пропорционально 2k. Распараллеливание допускает также алгоритм вычисления коэффициентов и значения интерполяционного полинома Ньютона. Для полинома от одной переменной временная сложность оценивается в [15], для полинома от двух переменных – в [6].
Об аналогах метода для уравнений других видов
Интерполяционным полиномом (7), преобразованным к виду (9), приближаются частные производные решения уравнения гиперболического типа второго порядка и выше, итерационное уточнение в этом случае выполнимо с помощью первообразной соответственной кратности. Для линейного гиперболического уравнения второго порядка такой подход реализован в [6]. Формально рассмотренный метод переносится на уравнения порядка выше первого на основе их преобразования в систему уравнений первого порядка. Пусть, например, рассматривается задача Коши для уравнения гиперболического типа
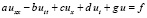 ,
,
где a, b, c, d, g, f – заданные функции независимых переменных x и t, ab > 0. Пусть приближенное решение ищется в прямоугольнике G из (1)–(3) при начальных условиях
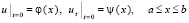 ,
,
где φ и ψ – заданные функции 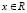 . Замена переменных влечет
. Замена переменных влечет
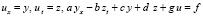 ,
,
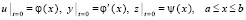 .
.
В каждой подобласти значения y и z из первых двух уравнений можно интерполировать полиномами (7) с преобразованием к виду (9). Для решения 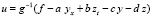 в качестве приближений частных производных подставляются соответственные частные производные преобразованных полиномов. Кроме того, используются полиномиальные приближения y, z. Процесс можно циклически повторять до достижения искомой точности. Вопрос о сходимости при данном подходе требует отдельного исследования.
в качестве приближений частных производных подставляются соответственные частные производные преобразованных полиномов. Кроме того, используются полиномиальные приближения y, z. Процесс можно циклически повторять до достижения искомой точности. Вопрос о сходимости при данном подходе требует отдельного исследования.
Аналогично итерационному уточнению можно строить последовательность приближений решения интегро-дифференциальных уравнений. Пусть, например, рассматривается задача Коши для линейного уравнения с интегральным оператором типа Вольтерры
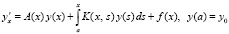 . (85)
. (85)
Предполагается, что A(x) и f(x) непрерывны при 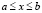 ,
, 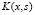 непрерывно при
непрерывно при 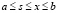 . В качестве нулевого приближения принимается
. В качестве нулевого приближения принимается 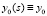 . С подстановкой
. С подстановкой 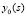 подынтегральную функцию можно интерполировать полиномом (7) с преобразованием к (9):
подынтегральную функцию можно интерполировать полиномом (7) с преобразованием к (9): 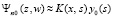 , где
, где 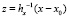 ,
, 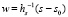 (здесь и ниже не индексируется подобласть и соответственные ей выражения). Тогда
(здесь и ниже не индексируется подобласть и соответственные ей выражения). Тогда 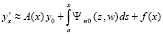 . Если
. Если 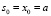 , то
, то 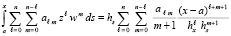 . Правую часть приближения
. Правую часть приближения 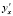 можно интерполировать полиномом Ньютона от одной переменной с равноотстоящими узлами, преобразовав его согласно [5] к виду алгебраического полинома с числовыми коэффициентами,
можно интерполировать полиномом Ньютона от одной переменной с равноотстоящими узлами, преобразовав его согласно [5] к виду алгебраического полинома с числовыми коэффициентами, 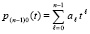 ,
, 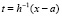 , h – шаг интерполяции. В результате
, h – шаг интерполяции. В результате 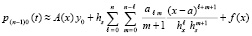 . Первообразная от
. Первообразная от 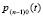 принимается за первое приближение:
принимается за первое приближение: 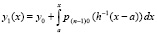 , или,
, или, 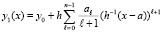 . Циклическое повторение описанного процесса с рекуррентными подстановками влечет
. Циклическое повторение описанного процесса с рекуррентными подстановками влечет 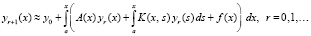 (знак
(знак 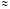 ставится, поскольку не учитываются остаточные члены интерполяции), отсюда
ставится, поскольку не учитываются остаточные члены интерполяции), отсюда 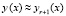 . Сходимость метода требует отдельного исследования.
. Сходимость метода требует отдельного исследования.
Задача (85) сводится к интегральному уравнению Вольтерры второго рода
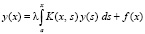 ,
,
где K(x, s) и f(x) – непрерывные функции при 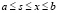 . Метод последовательных приближений для этого уравнения сходится к единственному непрерывному решению. Если в качестве нулевого приближения взять
. Метод последовательных приближений для этого уравнения сходится к единственному непрерывному решению. Если в качестве нулевого приближения взять 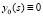 , то
, то 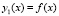 . Подынтегральную функцию с подстановкой y1 можно интерполировать полиномом (7) и преобразовать его к виду (9):
. Подынтегральную функцию с подстановкой y1 можно интерполировать полиномом (7) и преобразовать его к виду (9): 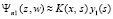 ,
, 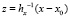 ,
, 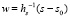 . Отсюда
. Отсюда 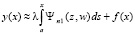 . Если
. Если 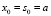 , то
, то 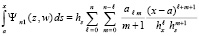 . Правую часть приближения y(x) можно интерполировать полиномом Ньютона от одной переменной, преобразовав его к виду
. Правую часть приближения y(x) можно интерполировать полиномом Ньютона от одной переменной, преобразовав его к виду 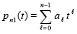 . Тогда
. Тогда 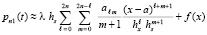 ,
, 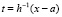 , и в качестве второго приближения принимается
, и в качестве второго приближения принимается 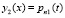 . В продолжение процесса, с рекуррентными подстановками, получится
. В продолжение процесса, с рекуррентными подстановками, получится 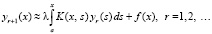 , откуда
, откуда 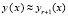 . Сходимость в данном случае можно анализировать, сопоставляя yr(x) со сходящейся последовательностью приближений, каждое из которых имеет точное аналитическое выражение.
. Сходимость в данном случае можно анализировать, сопоставляя yr(x) со сходящейся последовательностью приближений, каждое из которых имеет точное аналитическое выражение.
Для неоднородного уравнения Фредгольма 2-го рода 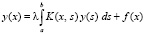 метод последовательных приближений сходится лишь при условии
метод последовательных приближений сходится лишь при условии 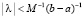 , где
, где 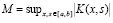 . Поэтому аналог рассмотренной схемы допустимо строить только при выполнении этого условия.
. Поэтому аналог рассмотренной схемы допустимо строить только при выполнении этого условия.
Заключение
Изложен метод кусочно-интерполяционного решения задачи Коши для уравнения переноса с итерационным уточнением. Решение и его частные производные интерполируются полиномами Ньютона от двух переменных, преобразуемыми к виду алгебраических полиномов с числовыми коэффициентами. На этой основе строится последовательное уточнение решения, которое сходно с двумерным аналогом последовательных приближений Пикара. В случае линейного уравнения переноса метод равномерно сходится к решению в прямоугольной области, строятся приближения частных производных. Приближение решения равномерно-непрерывно в данной области, кусочно-непрерывно – при ее делении на подобласти. Согласно эксперименту решение линейного и квазилинейного уравнений переноса в условиях гладкости приближается с абсолютной погрешностью 10-19–10-18. Метод отличается структурой и сравнительно малой погрешностью, что позволяет детализировать численное моделирование процесса переноса волны.