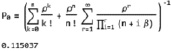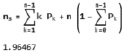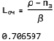Одной из важнейших компонент современного общества, обеспечивающих его жизнедеятельность и безопасность, являются так называемые системы массового обслуживания (СМО). От качества их функционирования зависит эффективность взаимодействия различных составляющих производственных, социально-экономических и технологических процессов, нацеленных на жизнеобеспечение человечества. Системы массового обслуживания нацелены на поддержание высокого уровня обслуживания отдельных индивидов, а в целом решают глобальные проблемы повышения эффективности функционирования сложных неоднородных социумов.
Настоящее исследование посвящено разработке математического обеспечения и отработке методологии компьютерного моделированию СМО с ограничениями по длине и продолжительности пребывания заявок в очереди на базе современных платформ символьной математики и имитационного моделирования.
Материалы и методы исследования
1. СМО с ограничением на длину очереди.
1.1. Одноканальные системы.
Рассмотрим одноканальную СМО, характризуемую следующими параметрами:
λ – интенсивнгость входящего потока заявок;
m – интенсивность обслуживания заявок в канале;
m – предельно допустимая длина очереди.
Диаграмма состояний одноканальной СМО с ограниченной длиной очереди может быть представлена следующим образом [1, 2]:
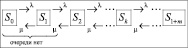
Состояния системы пронумерованы по числу заявок, находящихся в ней: S0 – канал свободен, заявок нет; 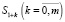 – канал занят, k заявок стоят в очереди.
– канал занят, k заявок стоят в очереди.
Поток заявок переводит систему из состояния 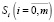 в состояние Si+1 с интенсивностью λ, а обратно – поток обслуживания с интенсивностью μ.
в состояние Si+1 с интенсивностью λ, а обратно – поток обслуживания с интенсивностью μ.
Если новая заявка поступает в момент, когда все т мест в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.
Очевидно, предельные вероятности состояний определятся следующим образом [2, 3]:
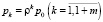 ,
,
где 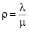 – коэффициент загрузки канала.
– коэффициент загрузки канала.
Из условия 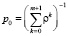 получим вероятность простоя канала
получим вероятность простоя канала 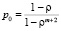 .
.
Относительная пропускная способность (вероятность того, что заявка будет обслужена) и абсолютная пропускная способность (число заявок, обслуживаемых в единицу времени) определятся по следующим формулам: 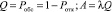 .
.
Выведем формулу для вычисления среднего числа заявок в системе (длины очереди). Очевидно, суммирование будет осуществляться с состояния S2, когда в очереди одна заявка, до состояния S1+m, в котором m заявок стоят в очереди.
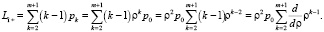
Выполнив элементарные преобразования, получим
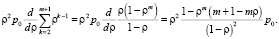
Таким образом, длина очереди определится следующим образом:
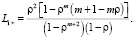
1.2. Многоканальные системы.
Исследуем n-канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью λ; интенсивность обслуживания равна m (для одного канала); максимально допустимое число мест в очереди равно m.
Возможные состояния многоканальной СМО с ограничением на длину очереди могут быть представлены следующей структурой [2, 3]:

Справа налево систему переводит поток, интенсивность которого равна интенсивности обслуживания, умноженной на число занятых каналов.
Выражения для предельных вероятностей состояний системы таковы:
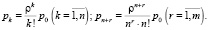
В данном случае вероятность простоя каналов обслуживания при отсутствии заявок определится следующим образом:
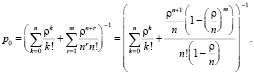
Соответственно, определятся выражения для вероятности отказа в обслуживании (заняты все n каналов и длина очереди m) 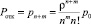 , относительной пропускной способности системы
, относительной пропускной способности системы 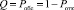 , абсолютной пропускной способности A = λQ, среднее число занятых обслуживанием каналов
, абсолютной пропускной способности A = λQ, среднее число занятых обслуживанием каналов 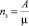 .
.
Получим формулу для вычисления среднего числа заявок в системе (длины очереди). Суммирование будет осуществляться с состояния Sn+1, когда в очереди одна заявка до состояния Sn+m в котором m заявок стоят в очереди.
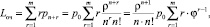
где 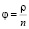 – интенсивность нагрузки канала.
– интенсивность нагрузки канала.
Преобразуем полученное выражение:
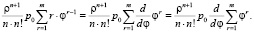
Далее, выполнив дифференцирование суммы убывающей прогрессии со знаменателем φ, получим
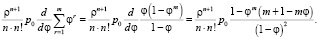
Окончательно длина очереди найдется по следующей формуле:
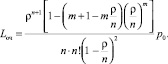
2. СМО с ограниченной продолжительностью пребывания заявок в очереди.
Для формализации описания функционирования систем с ограниченным временем ожидания их также удобно представлять в виде структуры состояний [4], которая по сути является схемой гибели и размножения

Здесь введены следующие обозначения: 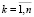 – число занятых каналов; r – число заявок, находящихся в очереди; ν – интенсивность уходящего из очереди (не дождавшись обслуживания) потока заявок.
– число занятых каналов; r – число заявок, находящихся в очереди; ν – интенсивность уходящего из очереди (не дождавшись обслуживания) потока заявок.
Для систем с ограниченным временем ожидания предельные вероятности состояний определяются по следующим формулам (здесь 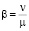 ):
):
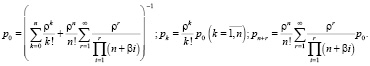
Исследуем формулу вероятности того, что система находится в состоянии S0 (все каналы свободны). Представим бесконечную сумму 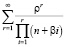 в виде двух слагаемых, в первом учитывается конечное число q – 1 ее элементов, а второе (бесконечная сумма) – остаток.
в виде двух слагаемых, в первом учитывается конечное число q – 1 ее элементов, а второе (бесконечная сумма) – остаток.
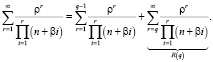
Можно получить оценку остатка сверху:
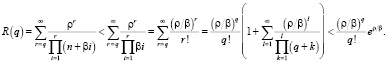
Результаты исследования и их обсуждение
Проведем практическую апробацию моделирования, например, СМО с ограниченным временем ожидания на унифицированном примере: система состоит из n = 3 каналов, интенсивность входящего потока составляет λ = 4 заявки, интенсивность обслуживания на каждом из каналов μ = 2 заявки. На основании статистических данных известна интенсивность досрочного ухода заявок из очереди v.
Компьютерное моделирование осуществлялось в пакете символьной математики Wolfram Mathematica. Фрагмент реализации компьютерной модели при v = 0,1 приведен в табл. 1.
Таблица 1
Фрагмент компьютерной модели
|
Вероятность простоя |
Число занятых каналов |
Длина очереди |
|
|
|
|
Использование пакета Wolfram Mathematica позволяет перенести в эту систему зависимости математической модели практически в исходном формальном представлении.
Оценку влияния величины интенсивности досрочного ухода из очереди на параметры функционирования СМО можно оценить на основании данных, представленных в табл. 2.
Таблица 2
Параметры функционирования СМО
|
Показатель Режим |
p0 |
Lоч |
tоч |
tСМО |
|
|
Без досрочного ухода из очереди |
0,111 |
0,889 |
0,222 |
0,722 |
|
|
Интенсивность ухода |
v = 0,1 |
0,115 |
0,707 |
0,177 |
0,677 |
|
v = 0,2 |
0,118 |
0,605 |
0,151 |
0,651 |
|
|
v = 0,3 |
0,120 |
0,536 |
0,134 |
0,634 |
|
В таблице tоч и tСМО определяют среднюю продолжительность пребывания заявок в очереди и в целом в системе обслуживания, соответственно.
Очевидно увеличение интенсивности досрочного ухода из очереди приводит к возрастанию вероятности простоя каналов обслуживания, уменьшению продолжительности пребывания заявок в системе и одновременно к снижению ее пропускной способности.
Результаты исследования зависимости вероятности простоя каналов и величины остатка R(q) от числа учитываемых членов в его разложении (при v = 0,1) приведены на рис. 1.
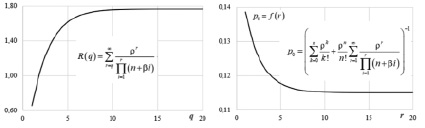
Рис. 1. Зависимость параметров от количества членов разложения
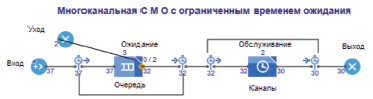
Рис. 2. Принципиальная схема модели
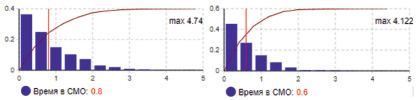
Рис. 3. Характеристики продолжительности пребывания заявок в СМО
Очевидно, наблюдается быстрая сходимость параметров к своим предельным значениям.
Исследование систем с ограниченным временем ожидания c уходом по TimeOut осуществлялось в среде пакета имитационного моделирования AnyLogic. На рис. 2 представлена принципиальная схема модели в среде пакета имитационного моделирования.
На текущий период моделирования в систему поступило 37 заявок, из них 30 покинули СМО после обслуживания, 3 ожидают в очереди, 2 находятся на обслуживании в каналах и 2 покинули систему из-за превышения допустимого времени ожидания в очереди.
На рис. 3 приведены гистограммы распределения времени пребывания заявки в СМО без ограничений и при досрочном уходе из очереди в случае превышения этого времени на 1 (для ранее заданных интенсивностей входящего потока заявок и их обслуживания).
Очевидно, ограничение предельно допустимого времени пребывания приводит к сокращению общего времени пребывания заявок в СМО и, одновременно, к уменьшению пропускной способности системы.
Выводы
Выполнен синтез математического описания функционирования систем массового обслуживания с ограничениями в виде:
– предельно допустимой для заявок длины очереди;
– заданной интенсивности досрочного ухода заявок из очереди без обслуживания;
– предельной продолжительности пребывания «нетерпеливых» заявок в очереди.
Представленные в работе математические модели, формальные зависимости и оценки апробированы и подтверждены в результате компьютерного и имитационного экспериментов, выполненных на базе системы символьной математики Wolfram Mathematica и аналитической платформы AnyLogic.
Анализу систем массового обслуживания с другими дисциплинами очереди посвящены современные исследования, например, в публикациях [5, 6].