Современная российская школа уже несколько лет (с 2011 г.) работает в условиях реализации новых федеральных государственных образовательных стандартов (ФГОС), кардинально изменивших представления о целях образования школьников и путях их достижения. Произошел переход к «стратегии социального проектирования и конструирования, от простой ретрансляции знаний к развитию творческих способностей обучающихся, раскрытию их возможностей, подготовке к жизни в современных условиях» [1, с. 8].
Достижение желаемого результата в познавательном и личностном развитии ребенка – формирование компетентной мотивированной личности – предполагает активную роль всех участников образовательного процесса и предъявляет новые требования к деятельности учителя и его педагогической квалификации. Большое значение, в частности, придается психологическим аспектам педагогического труда. У современного школьного учителя, наряду с традиционными функциями – обучать, организовывать, контролировать, оценивать, и др. – появились новые – планировать результаты обучения, на основе «выделения ожидаемого уровня актуального развития большинства обучающихся и ближайшей перспективы их развития, определять динамическую картину развития обучающихся, поощрять продвижения обучающихся, выстраивать индивидуальные траектории движения с учётом зоны ближайшего развития ребёнка» [1, с. 15].
Эффективная реализация этих функций требует освоения педагогом новых компетенций – в целеполагании (предметном и личностном), в разработке программ деятельности и их корректировке с учетом изменяющихся педагогических условий, в психологической диагностике личности и классного коллектива, в обработке и анализе диагностических данных с применением информационных технологий и др. Фактически квалифицированный учитель призван моделировать определенные условия образовательного процесса: выявлять его закономерности, представлять их в виде математических моделей и на этой основе прогнозировать результаты обучения и воспитания во временнóй перспективе.
Цель исследования: совершенствование мониторинга образовательного процесса в русле требований ФГОС [2] на основе построения и анализа моделей различных составных элементов образовательного процесса с использованием табличного процессора Microsoft Excel.
Материалы и методы исследования
Корреляционная связь между различными параметрами – это статистическая связь, при которой изменение среднего значения одного признака соответствует изменению среднего значения другого признака; она не является причинно-следственной, но указывает на более или менее согласованное изменение значений двух признаков.
Если при увеличении значений одного признака значения другого признака также увеличиваются – корреляция считается положительной, а если уменьшаются – отрицательной [3, c. 202].
При изучении корреляционной связи важно измерить ее тесноту с помощью коэффициента корреляции, например линейной корреляции К. Пирсона, и проверить уровень его значимости. В общем случае применяется следующая градация, характеризующая силу прямолинейной связи в зависимости от абсолютной величины коэффициента корреляции: если 0 ≤ ?rxy? < 0,3, то связь практически отсутствует; если 0,3 ≤ ?rxy? < 0,5, то связь слабая; если 0,5 ≤ ?rxy? < 0,7, то связь умеренная; если 0,7 ≤ ?rxy? < 1, то связь сильная; если ?rxy? = 1, то связь является функциональной. В математической статистике уровень значимости – это вероятность ошибки, которую можно допустить, принимая то или иное утверждение. Для педагогических исследований высказывания, имеющие вероятность ошибки р ≤ 0,05, называются значимыми [3, c. 207].
Для проверки значимости корреляционной связи необходимо вычислить значение статистики: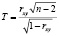 
, где rxy – коэффициент корреляции Пирсона, рассчитанный по выборке n. Если корреляционная связь незначима, то статистика Т имеет распределение Стьюдента с (п – 2) степенями свободы. Поэтому необходимо сравнить значение Т с критическим значением критерия Стьюдента tкрит. по заданному уровню значимости – 0,05 и числу степеней свободы – (п – 2). Если |T| < tкрит., то делается вывод – значение коэффициента корреляции статистически неотличимо от нуля. Если |T| ≥ tкрит., то коэффициент корреляции статистически значим: между переменными существует линейная связь [3, c. 207].
Результаты исследования и их обсуждение
Рассмотрим результаты диагностики личностных и познавательных универсальных учебных действий (УУД) [1, с. 20] обучающихся 3-го класса. В качестве примера возьмем такие значимые показатели, как «школьная мотивация», «школьная тревожность» (личностные УУД) и «словесно-логическое мышление» (познавательные УУД). Нас интересует, каким образом каждый из них влияет на учебную успешность (успеваемость) школьников.
Математическая обработка этого массива данных позволяет выявить следующие закономерности:
1. Взаимосвязь между исследуемыми параметрами развития школьников (на основе корреляционного анализа).
2. Тенденция изменения определенного параметра во времени (в сторону уменьшения или увеличения) – на основе регрессионного анализа.
3. Достоверность изменения определенного параметра во времени.
Рассмотрим расчет коэффициента корреляции и определение его значимости в MS Excel. Для проведения статистической обработки данных табличный процессор Microsoft Excel имеет большой набор встроенных статистических функций, а также подключаемую дополнительно программную надстройку «Пакет анализа» с различными модулями статистического анализа [4].
Пример 1. Определим, существует ли корреляция между следующими параметрами: уровнем развития школьной мотивации (данные по методике Н.Г. Лускановой), уровнем развития словесно-логического мышления (данные по методике Э.Ф. Замбацявичене), уровнем школьной тревожности (данные по методике А.М. Прихожан) и успеваемостью обучающихся (преобладающие оценки «отлично», «хорошо» и «удовлетворительно»). В диагностике участвовали 23 ученика 3 класса общеобразовательной школы (табл. 1).
Таблица 1
Результаты диагностики учеников 3-го класса
|
Уровень мотивации |
Уровень словесно-логического мышления |
Уровень тревожности |
Успеваемость |
|
|
1 |
2 |
2 |
2 |
3 |
|
2 |
5 |
3 |
3 |
4 |
|
3 |
2 |
2 |
1 |
3 |
|
4 |
3 |
4 |
2 |
4 |
|
5 |
4 |
4 |
3 |
5 |
|
6 |
3 |
3 |
3 |
3 |
|
7 |
4 |
4 |
2 |
5 |
|
8 |
3 |
3 |
2 |
3 |
|
9 |
3 |
3 |
4 |
4 |
|
10 |
2 |
3 |
2 |
3 |
|
11 |
3 |
4 |
3 |
4 |
|
12 |
4 |
4 |
2 |
5 |
|
13 |
3 |
3 |
1 |
3 |
|
14 |
5 |
4 |
4 |
5 |
|
15 |
4 |
4 |
2 |
5 |
|
16 |
4 |
3 |
2 |
4 |
|
17 |
4 |
3 |
2 |
4 |
|
18 |
5 |
4 |
2 |
4 |
|
19 |
2 |
3 |
1 |
3 |
|
20 |
4 |
3 |
3 |
5 |
|
21 |
4 |
4 |
3 |
5 |
|
22 |
2 |
4 |
2 |
3 |
|
23 |
2 |
3 |
3 |
3 |
Примечание: в столбце 2 цифрами 2, 3, 4, 5 обозначены уровни школьной мотивации: 2 – низкий, 3 – средний, 4 – выше среднего, 5 – высокий (1 – очень низкий уровень, в данной выборке отсутствует). В столбце 3 цифрами 2, 3, 4 обозначены уровни словесно-логического мышления: 2 – низкий, 3 – средний, 4 – высокий (1 – очень низкий уровень, в данной выборке отсутствует). В столбце 4 цифрами 1, 2, 3, 4 обозначены уровни школьной тревожности: 1 – чрезмерное спокойствие, 2 – нормальный, 3 – несколько повышенный, 4 – явно повышенный. В столбце 5 цифрами 3, 4, 5 обозначена успеваемость школьников: 3 – преобладают оценки «3», 4 – преобладают оценки «4», 5 – преобладают оценки «5».
В программе MS Excel открываем новый рабочий лист и переносим данные из табл. 1. MS Excel дает возможность провести корреляционный анализ с помощью различных инструментов. Рассмотрим один из возможных вариантов.
Чтобы вычислить коэффициент корреляции для переменных «Уровень мотивации» и «Успеваемость», используем встроенную функцию «КОРРЕЛ» (рис. 1, 2).
Получаем коэффициент корреляции rxy = 0,7666, который свидетельствует о наличии прямой и сильной корреляционной связи. Определим теперь, значима ли эта связь.
В нашем случае, после подстановки соответствующих величин в формулу получаем значении статистики Т = 7,2816. Значение tкрит. позволяет вычислить функция «СТЬЮДЕНТ.ОБР.2Х». В диалоговом окне данной функции открываются два поля для ввода значений: поле Вероятность – вводим значение уровня значимости р = 0,05 и поле Степени свободы – вводим значение 21 (так как наша выборка содержит 23 наблюдения) (рис. 3).
Получили tкрит. = 2,0796. Сравнив расчетное и критическое значения статистики Т, делаем вывод: найденный коэффициент корреляции – статистически значим. Аналогично, для пары переменных «Уровень словесно-логического мышления» и «Успеваемость» и для пары переменных «Уровень тревожности» и «Успеваемость» получаем соответственно следующие значения: rxy = 0,6372, Т = 4,8479 и rxy = 0,4315, Т = 2,6222, что также подтверждает значимость и этих коэффициентов корреляции.
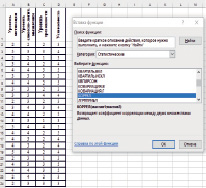
Рис. 1. Диалоговое окно функции «КОРРЕЛ» с данными диагностики
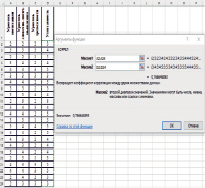
Рис. 2. Окно вывода функции «КОРРЕЛ»
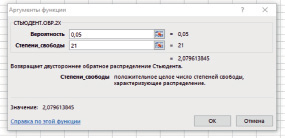
Рис. 3. Окно вывода функции «СТЬЮДЕНТ.ОБР.2Х»
Таким образом, мы выявили взаимосвязь успеваемости обучающихся данного класса с каждым из трех факторов (мотивация, тревожность, словесно-логическое мышление). В целях планирования результатов образовательного процесса важно выяснить, какой фактор вносит наибольший вклад в изменение успеваемости школьников. Ответ на этот вопрос может дать построение математических моделей этих взаимосвязей, например, с помощью регрессионного анализа в MS Excel.
Надстройка Пакет анализа MS Excel с модулем Регрессия позволяет достаточно эффективно моделировать взаимосвязи признаков [4, 5]. Во вкладке ДАННЫЕ запускаем команду Анализ данных и в открывшемся диалоговом окне выбираем модуль Регрессия.
После подтверждения выбора в окне модуля Регрессия заполняем поля ввода данных: Входной интервал Y – указываем расположение значений зависимой переменной «Успеваемость», Входной интервал Х – расположение значений независимой переменной «Уровень мотивации». Выбираем уровень надежности 95 %.
В окне вывода модуля Регрессия нас будут интересовать только значения коэффициентов и границы 95 % доверительных интервалов для них (рис. 4).
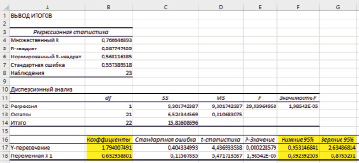
Рис. 4. Окно вывода модуля Регрессия пакета анализа MS Excel
Таким образом, мы получаем уравнение зависимости переменной Y – Успеваемость – от переменной Х – Уровень мотивации: Y = 0,63X + 1,79. Поскольку каждый из коэффициентов попадает в свой 95 %-ный доверительный интервал, то оба коэффициента признаются статистически значимыми на уровне значимости р = 0,05 (в противном случае коэффициент признается статистически не отличимым от нуля).
Аналогично получаем уравнение зависимости переменной «Успеваемость» от переменной «Уровень словесно-логического мышления»: Y = 0,84Х + 1,12; и уравнение зависимости переменной «Успеваемость» от переменной «Уровень тревожности»: Y = 0,44Х + 2,88. Сравнивая коэффициенты при Х в данных уравнениях (0,63; 0,84 и 0,44), мы можем сделать вывод, что наиболее существенный вклад в изменение успеваемости вносит второй фактор – уровень словесно-логического мышления (коэффициент 0,84), в меньшей степени – уровень школьной мотивации (коэффициент 0,63) и уровень тревожности (коэффициент 0,44). Подобным образом можно исследовать взаимосвязь и других факторов (например, особенностей общения учителя с уровнем тревожности школьников), что дает представление о закономерностях образовательного процесса в данном классе, тенденциях в развитии детей, позволяет прогнозировать ближайшие результаты обучения и воспитания и на этой основе корректировать образовательные программы.
Во многих случаях требуется установить не наличие взаимозависимости между переменными, а наоборот, имеется ли статистически значимое различие между выборками по уровню выраженности признака. Такая задача может возникнуть, если требуется проследить изменения во времени по каким-либо показателям для одного и того же класса.
Пример 2. Учитель провел два диагностических среза (в мае 2015 г. и в мае 2016 г.) особенностей самооценки обучающихся своего класса (по методике «Лесенка» В.Г. Щур) (табл. 2). Выявилась следующая динамика показателей: число детей с заниженной самооценкой снизилось на 4,3 % (с 8,7 % во втором классе до 4,3 % в третьем классе), число детей с адекватной самооценкой увеличилось на 17,4 % (с 43,5 % до 60,9 % соответственно), число детей с завышенной самооценкой уменьшилось (с 47,8 % до 34,8 % соответственно). Можем ли мы утверждать, что изменения показателей самооценки младших школьников статистически значимы?
Таблица 2
Результаты диагностики самооценки учеников
|
Испытуемый |
2 класс (май 2015 г.) |
3 класс (май 2016 г.) |
|
1. Оля А. |
1 |
2 |
|
2. Вика Б. |
2 |
2 |
|
3. Саша Б. |
2 |
2 |
|
4. Дима В. |
2 |
2 |
|
5. Аня В. |
2 |
2 |
|
6. Дима Г. |
2 |
2 |
|
7. Илья Д. |
3 |
3 |
|
8. Вова З. |
2 |
2 |
|
9. Ира К. |
3 |
3 |
|
10. Катя К. |
2 |
2 |
|
11. Андрей К. |
3 |
2 |
|
12. Маша Н. |
1 |
1 |
|
13. Наташа П. |
3 |
3 |
|
14. Игорь П. |
3 |
2 |
|
15. Саша Р. |
2 |
2 |
|
16. Лиза С. |
3 |
3 |
|
17. Максим Т. |
3 |
3 |
|
18. Юля Т. |
2 |
2 |
|
19. Егор Т. |
3 |
3 |
|
20. Оксана Х. |
3 |
3 |
|
21. Алёна Ц. |
2 |
2 |
|
22. Максим Ш. |
3 |
3 |
|
23. Аня Ш. |
3 |
3 |
Примечание: в столбцах 2 и 3 цифрами 1, 2, 3 обозначены уровни самооценки: 1 – низкий (заниженная самооценка), 2 – средний (адекватная самооценка), 3 – высокий (завышенная самооценка).
Для выявления статистической значимости (достоверности) различия между двумя выборками по уровню выраженности исследуемого признака наиболее часто применяется t-критерий Стьюдента. Применив встроенную функцию «СТЬЮДЕНТ.ТЕСТ», мы можем вычислить достоверность различий между выборками (показателями самооценки в конце второго и в конце третьего классов).
После подтверждения выбора в открывшемся диалоговом окне данной функции в полях Массив 1 и Массив 2 мы указываем расположение соответственно данных первого и последнего столбцов, в поле Хвосты вводим значение 2, что означает двусторонний тест, в поле Тип – значение 1 (парный тест) (рис. 5).
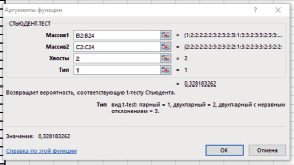
Рис. 5. Окно вывода функции «СТЬЮДЕНТ.ТЕСТ»
Получили уровень значимости р = 0,328, что значительно больше граничного; следовательно, различие между выборками по уровню выраженности признака не может быть признано достоверным. Если сравнивать показатели самооценки школьников в процентном соотношении (традиционный способ обобщения данных), то напрашивается вывод о положительной динамике. Но этот вывод ошибочен, поскольку различие значений изучаемых параметров статистически незначимо, случайно.
Заключение
Таким образом, использование педагогом информационных технологий открывает новые возможности совершенствования мониторинга образовательного процесса: выявлять взаимосвязи различных его составляющих, правильно интерпретировать данные диагностики УУД обучающихся, прогнозировать тенденции в их развитии, выстраивать корректную стратегию учебно-воспитательной работы.
Рассмотренные нами методы анализа данных на основе программного продукта MS Excel являются начальной ступенью повышения информационной культуры педагога, их освоение и дальнейшее развитие позволяет сделать процесс реализации новых ФГОС более эффективным.