Вся история человечества характеризуется настойчивыми попытками описания окружающего мира в строго фиксированных категориях. Философские рассуждения каждой эпохи сводились к поиску первопричин, литература – к отражению наиболее актуальных проблем своего периода. Широко известные легенды и мифы Древней Греции – это не что иное, как систематизация частичных представлений о мире в художественной форме, выражающая непоколебимую идею об упорядоченности и обусловленности событий. С развитием точных и естественных наук произошел раздел сфер влияния, так что несмежные области знания начали говорить практически на разных языках. Лишь с рождением таких понятий, как «системный подход» и «системные исследования», междисциплинарность и диффузия одних наук в другие стали очевидными и рациональными в научном сообществе. Параллельно с этим начали набирать силу такие направления, как имитационное моделирование, исследование операций, синергетика [1]. К настоящему моменту взаимное влияние преобразило самую суть смежных дисциплин и размыло границы между ними.
Моделирование технологических систем и процессов – несравненно более узкая сфера изысканий, имеющая, тем не менее, колоссальное влияние на жизнь общества. Централизованное производство тепловой и электрической энергии априори требует высокой степени внимания к показателям надежности, безопасности, эффективности и экологичности. Многие объекты топливно-энергетического комплекса относятся к категории многосвязных нестационарных нелинейных объектов управления, и на данный момент разработано множество подходов к моделированию подобных систем. Так, в статье [2] описан классический подход к построению математических моделей многосвязных объектов управления, состоящий в переходе от качественных зависимостей между переменными объекта к структурированной формализации задачи. В работе [3], напротив, предпочтение отдается перспективным методам управления ГТУ – адаптивной САУ с эталонной моделью, САУ с применением нечеткой логики и управляющей системе, основанной на нейронных сетях.
Рассматривая модель с позиции ее использования в процессе автоматического управления, авторы склоняются к использованию гибридной модели, включающей в себя аппарат теория автоматического управления, классического дифференциального исчисления и технологий искусственного интеллекта. Целью данной работы является анализ современных подходов к построению моделей многосвязных объектов, перспектив использования гибридных алгоритмов в данном контексте.
Материалы и методы исследования
В статье [4] авторами рассматривался подход, основанный на декомпозиции технологического объекта или технологического процесса и представлении каждой части в виде некоторого функционального блока. Предполагалось, что блоки воздействуют друг на друга с помощью потоков различной природы – энергии, вещества, а также информации – а потому могут определять некоторые операции над потоками. Рассматриваемая система – паровой котел в составе парогазовой установки – представляет собой многосвязную нелинейную нестационарную систему, в которой основное значение имеют потоки теплоносителей. Эти потоки в системе движутся по индивидуальным траекториям, пересекая блоки в определенном порядке и взаимодействуя в пределах каждого блока между собой, а также напрямую с самой системой, косвенно – с окружающей средой. Таким образом, можно утверждать, что на характер взаимодействий внутри блока оказывают влияние три группы величин:
1. Характеристики потоков.
2. Характеристики среды взаимодействия – то есть самого блока.
3. Внешние причины, не относящиеся ни к блоку, ни к рассматриваемым потокам (это могут быть неучтенные факторы, в частности неучтенные потоки).
На данном этапе будем рассматривать каждый поток и сам блок как объекты с сосредоточенными параметрами, но, как отмечалось ранее, нестационарные. Процессы внутри блока могут быть описаны следующей системой уравнений в изображениях по Лапласу:
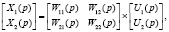 (1)
(1)
где U1(p) – изображения некоторого входного параметра первого потока; U2(p) – изображения входного параметра второго потока; X1(p) – изображения некоторого выходного параметра первого потока; X2(p) – изображения выходного параметра второго потока; Wij(p) – передаточная функция, связывающая изменение выходного параметра i с изменением входного параметра j. Движение потоков теплоносителей в общем случае предполагает прохождение различных последовательностей блоков. В пределах каждого блока процессы взаимодействия могут быть описаны с помощью передаточных функций – по четыре на каждый блок. Для использования этих передаточных функций в вычислительном эксперименте необходимо определить как их типы, так и определяющие параметры. Рассматриваемая многосвязная система может быть описана структурной схемой следующего вида (рисунок).
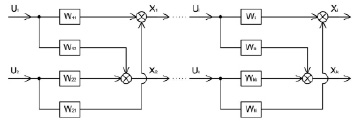
Структурная схема многосвязного объекта управления с двумя потоками теплоносителей – потоком пара (воды) и потоком дымовых газов
Проанализируем смысловую нагрузку каждой передаточной функции:
– W11 (как и Wii) связывает изменение выходного параметра первого потока с входным параметром того же потока – эта передаточная функция не учитывает взаимодействие потоков между собой, но акцентирует внимание на взаимодействии потока со средой;
– W22 (как и Wkk) связывает изменение выходного параметра второго потока с входным параметром того же потока – по смысловому значению эта передаточная функция аналогична W11;
– W12 (как и Wik) связывает изменение выходного параметра второго потока с входным параметром первого потока – эта передаточная функция учитывает взаимодействие потоков между собой, не учитывая их взаимодействие со средой;
– W21 (как и Wki) связывает изменение выходного параметра первого потока с входным параметром второго потока – по смысловому значению эта передаточная функция аналогична W12.
Будем исходить из физической и химической природы процессов, происходящих в системе, при решении задач структурной и параметрической идентификации. На данном этапе будем рассматривать передаточные функции без запаздывания. Взаимодействие потоков со средой не предполагает теплообмен, однако, поскольку движение теплоносителей происходит в каналах, потоки теряют энергию на преодоление линейных и местных гидравлических сопротивлений. В пределах одного блока линейные участки могут чередоваться с местными сопротивлениями, и общие потери давления в результате движения по такому участка для потоков рассчитываются по формуле
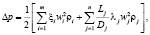 (2)
(2)
где wi, wj – скорость потока на i-м и j-м участках соответственно, м/с; ρi, ρj – плотность потока на i-м и j-м участках соответственно, кг/м3; ξi – коэффициент местного гидравлического сопротивления на i-м участке; Lj – характеристическая длина j-го участка, м; Dj – характеристический диаметр j-го участка, м; λj – коэффициент Дарси (коэффициент потерь на трение по длине) j-го участка. Перепад давления, испытываемый на участке, может быть измерен при различных скоростях и температурах потока, а затем по экспериментальным значениям ?p, w, T могут быть определены функциональные зависимости. С большой долей вероятности можно предположить, что прямое или косвенное измерение температуры и скорости потока производится не на всех локальных участках, общее количество которых равно m + n. Совокупность участков неоднородна, сложна и характеризуется следующими особенностями:
1. Участки неравномерны как по геометрическим, так и по техническим свойствам, а потому вносят различный вклад в изменение параметров потока.
2. Изменение целевого параметра не обязательно является монотонной функцией пройденного поток пути.
3. Количество участков, которое может быть выделено, является произвольным, поэтому необходим некоторый критерий, задающий условие остановки дробления.
Усреднение скорости потока в качестве одного из возможных решений означает постоянство режима течения, что в свою очередь отразится на модели теплообмена между потоками. Уравнения, описывающие турбулентный режим движения жидкости или газа по сравнению с ламинарным режимом имеют корреляции, вызванные не только пульсациями скорости, но и пульсациями плотности и температуры, при этом для замыкания системы уравнений требуются дополнительные соотношения [5]. Очевидно, что эта часть модели требует подробного изучения и принятия специального решения.
Для описания взаимодействия между потоками теплоносителей можно попытаться использовать апериодическое звено первого порядка, что требует на этапе параметрической идентификации вычисления четырех неизвестных параметров (коэффициенты W12 и W21). В работе [4] было предложено использовать следующее определения постоянной времени, полученное на основе подобия физических процессов:
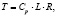 (3)
(3)
где L – характеристический размер рассматриваемого объема газовой смеси в блоке, м; cp – изобарная теплоемкость газовой смеси, Дж/(м3·К); R – термическое сопротивление в блоке, К·c·м2/Дж. Для расчета изобарных теплоемкостей были аппроксимирующие функции, термическое сопротивление является величиной, обратной коэффициенту теплопередачи, характеристический объем в связи с неопределенностью состояния потока подлежит уточнению.
Коэффициент теплопередачи характеризует интенсивность взаимодействия потоков и определяет теплообмен между ними. Примем за основной параметр потока температуру. Поскольку значения температур потоков на выходе и выходе из блока предполагаются известными или рассчитанными, то коэффициент может быть вычислен, казалось бы, банальным отношением температуры на выходе к температуре на входе. Такой расчет имеет три серьезных недостатка:
1. Не учитываются инерционные свойства потоков.
2. Не учитываются транспортные запаздывания.
3. Коэффициенты передачи зависят от самих температур потоков и от множества других факторов, причем учесть все в полной мере априори невозможно.
Следовательно, процесс теплообмена также требует некоторого приближения.
Результаты исследования и их обсуждение
Нужно отметить, что в целом нас интересует некоторая интегральная характеристика взаимодействия, построенная на основе усредненных параметров потоков. Основная сложность заключается в моделировании самих потоков. Поскольку поток представляет собой ключевую фигуру в предлагаемой концептуальной модели, рассмотрим возможные варианты его описания. На текущий момент в качестве базы имитационного моделирования выделяют четыре парадигмы: дискретно-событийное моделирование, динамическое моделирование, системная динамика в смысле Форрестера и мультиагентный подход. При этом все четыре компонента используют причинно-следственный механизм продвижения процессов во времени, а отличия заключаются в оперировании различными наборами объектов [6].
Известно, что параметры, определяющие тепловые процессы, носят неопределенный интервально стохастический характер. В работе [7] предложен метод моделирования, основанный на получении уравнений для статистических мер (математических ожиданий, дисперсий, ковариаций) тепловых процессов при заданных статистических мерах входных интервально стохастических определяющих параметров. Однако в данной работе предполагается разбиение системы на совокупность изотермических элементов, находящихся во взаимодействии между собой, в то время как принятая концепция предполагает изобарные и неизотермические процессы. К тому же предлагаемые изотермические элементы располагаются неподвижно в пространстве, что совершенно отличает их от потоков, которые движутся с переменной скоростью и взаимодействуют друг с другом в различных сечениях.
Очевидно, что описание потока в каждой его точке при заданном уровне дискретизации является избыточным с позиции процесса управления – требуются лишь некоторые интегральные характеристики потоков. Кроме того, следует учитывать зашумленность измеренных сигналов. Все вышеперечисленное наталкивает на мысль использования нечеткой логики для устранения неопределенности в определении характеристик потока. Нечеткая логика особенно уместна, когда процесс сложен, не полностью известен, медленен и труден для моделирования аналитически или экспериментально [8]. Основное требование, однако, заключается в том, что должна быть доступна база знаний. Использование нечетких множеств при высокой степени гранулированности информации позволяет сократить объем обрабатываемой информации и тем самым ускорить вычисления [9]. Для обучения нечеткой модели потока можно использовать методы, основанные на использовании нейронечетких сетей.
В статье [10] рассматривается моделирование поведения газа с помощью клеточного автомата, функционирующего в режиме синхронной работы. На каждом шаге по времени изменение состояния происходит в два этапа: сначала происходит перемещение частиц в соседние узлы (этап сдвига), а затем соударение частиц в узлах (этап столкновения). Эффективность применения клеточных автоматов привела к большому разнообразию их типов, описываемых во множестве публикаций. Так, в исследовании [11] демонстрируется применение нечеткого клеточного автомата для регулирования поля температуры. Показано, что задачу расчета поля температуры в динамических условиях можно решить с помощью нечетких клеточных автоматов без памяти или нечетких комбинационных схем. Матричный подход нечеткой логики позволяет достичь большей гибкости в использовании аппаратных ресурсов, чем вычислительный метод, основанный на решении интегро-дифференциальных уравнений.
Заключение
Проведенный анализ позволяет сделать вывод, что предлагаемая авторами концепция построения блочной модели парового котла может быть реализована в виде гибридной информационной системы, основанной на применение операторного исчисления и подкрепленной методами искусственного интеллекта. Результаты подобного синтеза будут представлены в последующих работах.



