При разработке прогнозов эксплуатационной безопасности технических объектов, особенно прогнозов, обеспечивающих предупреждение аварийных отказов, отказов с катастрофическими исходами, необходима надёжная и точная модель прогноза, учитывающая индивидуальные данные объекта, работающего в индивидуальных условиях эксплуатации.
Цель исследования: обеспечение надёжности и повышение точности прогнозов эксплуатационной безопасности технических систем, определение остаточного ресурса и момента отказов.
Задача настоящей работы – при формировании прогнозов конкретного объекта с ростом продолжительности наблюдения за ним обратить внимание на динамику изменения параметров устанавливаемых закономерностей деградации, на изменение вида закономерностей и даже на исключение одних видов и переход на другие модели, наиболее точно отражающие исследуемые явления непосредственно в процессе эксперимента. Таким образом, обеспечиваются более качественные и достоверные показатели прогноза.
Материалы и методы исследования
Объектом исследования является деградационное изменение технических устройств в процессе эксплуатации. Предмет исследования – прогноз эксплуатационной безопасности технических устройств.
Фиксируя количественные значения характеристических показателей конкретного объекта, отражающие его деградационное изменение в индивидуальной истории эксплуатации, формируют временные ряды. Аппроксимируя временные ряды по методу наименьших квадратов различными функциями, устанавливают аналитические виды закономерностей изменения характеристических показателей. Формируют модели. В динамике наблюдения эксплуатационного изменения объекта с увеличением объёмов совокупностей экспериментальных данных уточняют и корректируют параметры моделей. Для сравнительного анализа моделей и выделения моделей с лучшими показателями качества прогнозов предложены статистические критерии. Путем экстраполяции выполняют индивидуальный прогноз изменения объекта в конкретных условиях его эксплуатации, определяют остаточный ресурс и устанавливают моменты отказа.
Результаты исследования и их обсуждение
Для каждого технического объекта можно определить параметры, называемые характеристическими, по изменению которых можно судить о деградационном состоянии объекта. Формируя математическую модель деградационного изменения характеристического параметра объекта, можно установить его закономерность, оценить остаточный ресурс и определить таким образом момент отказа [1, 2].
Абсолютно разные модели для ограниченного множества экспериментальных данных деградационного изменения характеристического параметра могут обеспечить одинаковые математические критерии прогноза, однако результаты прогнозов у них могут быть совершенно различны.
Пусть экспериментально получены данные для 10 первых точек изменения характеристического параметра (табл. 1).
Таблица 1
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
х, ед. |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
yэ |
3,6 |
16,1 |
27,0 |
36,5 |
44,8 |
52,0 |
58,2 |
63,6 |
68,3 |
72,4 |
При аппроксимации таблицы экспериментальных точек yэ по методу наименьших квадратов (МНК) наибольшую точность обеспечили экспоненциальная функция y1 и полином третьей степени y2 [3–5]:
y1 = 99,6-96e-0.07x
и
y2 = 3,58 + 6,64x – 0,21x2 + 0,003x3.
В области задания обе функции имеют средние квадратические отклонения одного порядка, равные: σ1 = 0,055, σ2 = 0,039.
Анализ динамики изменения значений экспериментальных данных показывает, что они имеют характер насыщения. Функцию насыщения отражает экспоненциальная зависимость y1. Кубическая парабола y2 в области задания обеспечивает меньшее среднее квадратическое отклонение σ2 < σ1. однако, при х = 50 она показывает физически противоречивый результат.
Для оценки точности моделей и качества прогноза целесообразно использовать следующие три критерия.
1. Среднее квадратическое отклонение между экспериментальными значениями и значениями, полученными по аппроксимирующей функции, называемое погрешностью аппроксимации:
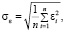
где εi = ypi – yэi,
ypi, yэi – значения исследуемой функции расчетное и экспериментальное в i-й точке.
2. Коэффициент детерминации D:
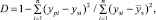(1)
где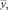 
– среднее значение экспериментальной функции.
Коэффициент детерминации D показывает, насколько точно аппроксимированы исходные данные функцией, выражающей закономерность процесса, функцией прогнозирования. Из анализа расчетной формулы (1) следует, что при абсолютном совпадении расчетной аппроксимирующей функции yp c экспериментальной yэ во всех точках для любого i ypi = yэi, числитель дроби равен нулю, а значение D = 1. Если коэффициент детерминации D имеет значение, близкое к 1, то считают, что функция прогноза достаточно точно описывает (приближает) экспериментальную функцию «в прошлом», а потому вычисленные значения yp для будущих моментов времени, также будут соответствовать реальным величинам. Для табл. 1 и аппроксимирующих функций y1 и y2 значения коэффициентов детерминации соответственно равны:
D1 = 0,999993691, D2 = 0,999996814.
Оба коэффициента детерминации практически равны единице, оба «свидетельствуют» о точном прогнозе в будущем. Однако это не так. Нужно исследовать третий критерий – доверительный интервал L.
3. Доверительным интервалом L для прогнозного значения называется случайный интервал, который с заданной вероятностью α содержит неизвестное точное значение функции у(х). Вероятность α называется доверительным уровнем или надёжностью. Для оценки доверительных интервалов нужно вычислить:
а) расчетные значения прогнозируемых величин в заданные моменты времени. Пусть задан момент x0 = 50; расчетные значения исследуемых функций в этой точке абсолютно разные: y1p(50) = 96,7 y2p(50) = 185,58.
б) среднее арифметическое аргумента и сумму квадратов его отклонений от среднего:
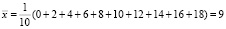
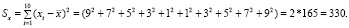
в) стандартные ошибки прогноза
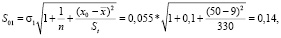
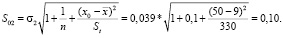
г) границы доверительного интервала можно оценить с использованием распределения Стьюдента, но в практических оценках рекомендуют ширину ? интервала выбирать равной ? = 3S0 при α = 0,95 (согласно эмпирическому правилу «три сигма»). Таким образом, для аппроксимирующих функций y1 и y2 получим
;
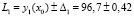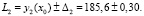
Очевидно, что расчетные значения третьего критерия тоже близки.
В рассмотренном примере при значениях средних квадратических отклонений и стандартных ошибок прогноза одного порядка, при практически одинаковых значениях коэффициентов детерминации и при близких доверительных интервалах, тем не менее значения прогнозных величин существенно различны. То есть при верных вычислительных алгоритмах показана опасность применения математических методов прогнозирования без пошагового анализа их промежуточных результатов в последовательности всех режимов испытаний, показана возможность грубейших ошибок долгосрочного прогноза.
При реализации прогнозирования для исключения указанной выше опасности необходимо выполнить следующее.
1. Разработать план эксперимента с оптимальной дискретностью контрольных испытаний.
2. Выбрать аппроксимирующую функцию (или функции) с наилучшими показателями по всем трем вышеуказанным критериям.
3. Мощным средством для анализа, сравнения, коррекции и уточнения моделей прогноза является рекурсивное прогнозирование. В соответствии с его рекомендациями из получаемых данных выделяют последние значения, определяют по ним прогнозы, сравнивают с реальностью.
Такой прием «пристрелочного прогноза» позволяет оценить точность будущего прогноза на реальных данных. В случае расхождений следует выполнять анализ причин их возникновения. «Пристрелочный прогноз» нужно выполнять в процессе всего эксперимента. Добавляя в исходные данные результаты нового последнего контрольного испытания, уточняют параметры аппроксимирующих моделей. Здесь также целесо- образен анализ и контроль динамики изменения параметров моделей (коэффициентов аппроксимирующих функций). Если при последовательном пересчете параметров модели они остаются достаточно стабильными или монотонно стремятся к определённому значению предела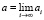 
, то можно считать, что модель верно отражает закономерность процесса.
Результаты вычислительного эксперимента по определению влияния количества экспериментальных точек на параметры аппроксимирующих функций показаны на примере короткого замыкания витков индуктивных элементов. Зависимость выходного тока yэ во времени (ось х) представлена в табличной форме (табл. 2) [6].
Таблица 2
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
x, ед. |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
38 |
40 |
|
yэ |
0,0 |
0,67 |
1,56 |
2,78 |
4,54 |
7,35 |
12,5 |
25,0 |
47,5 |
100,0 |
Если использовать начальный участок для пяти точек, то в результате полиномиальной аппроксимации получены следующие полиномы первой очереди:
;
;
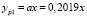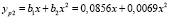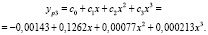
Для сравнительного анализа точности аппроксимации поточечно вычислены значения yр1, ε1, yр2, ε2, yр3, ε3 и построены графики (рис. 1).
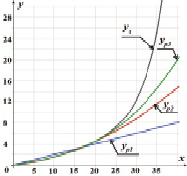
Рис. 1. Сравнительный анализ аппроксимирующих и экспериментальной функций при ограниченном начальном участке. yэ – график экспериментальной функции; yp1 – линейная аппроксимация; yp2 – квадратичная аппроксимация; yp3 – аппроксимация кубической параболой
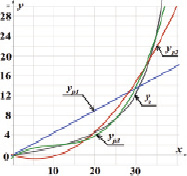
Рис. 2. Сравнительный анализ аппроксимирующих и экспериментальной функций при пролонгированном начальном участке. yэ – график экспериментальной функции; yp1 – линейная аппроксимация; yp2 – квадратичная аппроксимация; yp3 – аппроксимация кубической параболой
Анализ графиков (рис. 1) показывает, что наилучшие результаты в совпадении экспериментальной и расчётных зависимостей обеспечивает в области x ≤ 20 полином 3-й степени. Однако для всех полиномов ошибка сильно растёт в точках прогноза (в 6-й и в 7-й). Наименьшую погрешность в этих точках также обеспечивает кубическая парабола.
Если увеличить начальный участок до восьми точек, то в результате полиномиальной аппроксимации получаются следующие полиномы второй очереди:
;
;
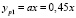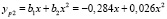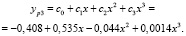
Для сравнения точности аппроксимации полиномов 2-й очереди поточечно вычислены значения yp1, ε1, yp2, ε2, yp3, ε3 и построены графики (рис. 2).
Сравнительный анализ аппроксимирующих функций 1-й и 2-й очереди показывает существенное изменение параметров. Оно обусловлено существенным изменением характера экспериментальной зависимости, появлением участка с крутым фронтом роста.
Погрешности кубической параболы во 2-й очереди существенно возросли, но эта функция остаётся наилучшей среди всех исследуемых многочленов.
Анализ графиков показывает также, что погрешности многочленов yp1 и yp2 настолько велики, что их использование для дальнейших расчетов нецелесообразно. Появление крутого фронта роста в экспериментальной функции может свидетельствовать о лавинном характере развития процесса. Если аппроксимировать экспериментальную функцию yэ для n = 5 точек дробно-рациональной функцией, то будет получена функция:
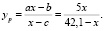
Для неё поточечно вычислены значения yp и ε, и дальнейший анализ показал, что дробно-рациональная функция наилучшим образом аппроксимирует экспериментальную функцию во всем диапазоне исследования. Полученная на основе пяти начальных экспериментальных точек при табулировании, она показала практическое совпадение для всех точек полного ресурса. В сравнении с этой функцией точность аппроксимирующего полинома yp3 существенно ниже.
Таким образом, продемонстрированы проблемы и методы обеспечения реальных прогнозов изменения характеристических показателей, получаемых в эксперименте. Особенно следует подчеркнуть, что для качественного прогнозирования целесообразно сформировать несколько моделей исходных данных, постоянно анализировать их точность и достоверность в процессе эксперимента, при необходимости изменять дискретность контрольных испытаний, корректировать и обоснованно выбрать модели, отражающие реальную динамику процессов с наибольшей достоверностью.
Выводы
1. Для решения задач прогноза деградационных изменений характеристических параметров технических объектов эффективен регрессионный МНК к формированию математической модели, с отражением всей последовательности режимов работы объекта и рекуррентным учетом всех предыдущих режимов в каждой последующей точке.
2. Установлена целесообразность формирования нескольких моделей, отражающих закономерности исследуемых процессов. При реализации эксперимента необходим анализ стабильности параметров моделей или учет их изменения, коррекции и даже исключения или замены некоторых моделей в целом.
3. Проведён сравнительный анализ моделей прогноза – аппроксимирующих функций, построенных по МНК. Показано, что параметры этих функций существенно зависят от числа точек наблюдения. Добавление текущей точки может существенно изменить параметры моделирующей функции. С учётом последующих участков наблюдения может измениться вид моделирующей функции. Приведены критерии качества моделей прогноза.