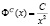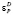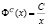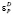Рассматривая логистические процессы, агенты (производители, посредники и конечные потребители) торгово-посреднической сети (ТПС) обращают внимание не только на свои потенциальные возможности, но и на реакцию свободного рынка конкурирующих товаров. Важное место здесь занимают спрос и предложение. В классических моделях микроэкономики [1] рассматривается точка равновесия, образованная пересечением линий спроса и предложения, которая определяет цену товара и объем продаж. Если под воздействием факторов эта точка покидает равновесное состояние и путем управляющих воздействий должна вернуться в исходное состояние или близкое к нему, то речь идет об устойчивости системы. Движение точки имеет колебательный характер с равными по величине отклонениями справа и слева от точки равновесия. В этом случае будем иметь идеальный случай устойчивости, который подтвердится нормальностью закона распределения случайной величины таких показателей, как цена и объем продаж. В реальных условиях функционирования рынка можно предположить, что вид линии и, следовательно, функцию спроса можно построить исходя из покупательского спроса при различных ценах на один и тот же товар. Но вид линии предложения, как правило, неизвестен, и его практически невозможно оценить по наблюдениям за состоянием рынка [2].
Цель исследования заключается в разработке упрощенной математическая модели построения линий спроса с учетом возможных закономерностей распределения статистических данных в процессе функционирования микрорынка для агентов торгово-посреднической сети.
В системе поставок и реализации продукции на спрос и предложение оказывает немаловажное значение количество факторов влияния, что не позволяет четко судить о наличии той или иной закономерности распределения случайной величины [3]. Следовательно, на множестве 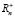 будем иметь множество точек, отображение которого на
будем иметь множество точек, отображение которого на 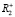 представляет собой поле (хаотично разбросанных) точек с координатами (P;Q), где P – цена товара, Q – объем приобретённого на рынке товара. Попытка установить корреляционную связь между данными параметрами вряд ли увенчается успехом. В таких случаях построение функций спроса затруднительно. Тем не менее, решая задачу планирования поставок, агенты сети вынуждены учитывать спрос на товарном рынке. Далее в данной работе рассматривается упрощенная математическая модель построения возможных линий спроса на
представляет собой поле (хаотично разбросанных) точек с координатами (P;Q), где P – цена товара, Q – объем приобретённого на рынке товара. Попытка установить корреляционную связь между данными параметрами вряд ли увенчается успехом. В таких случаях построение функций спроса затруднительно. Тем не менее, решая задачу планирования поставок, агенты сети вынуждены учитывать спрос на товарном рынке. Далее в данной работе рассматривается упрощенная математическая модель построения возможных линий спроса на 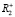 , не требующая знаний о линии предложения, но использующая знание факторов потребительского спроса.
, не требующая знаний о линии предложения, но использующая знание факторов потребительского спроса.
Модель построения линий спроса
Если представить ТПС в виде графа сети, то его простейшее изображение имеет ребра/ветви – агенты и вершины/узлы – микрорынки, на которых осуществляется процесс купли-продажи. Микрорынки характеризуются показателями: P – цена единицы товара; Q – объем реализации товара при данной цене. Агент, связывающий микрорынки между собой, характеризуется количеством приобретенного и реализованного товара (производитель только реализует товар, конечный потребитель только приобретает его). Соотношение этих показателей позволяет рассчитать коэффициент R указывающий, в каком соотношении находится сложившийся спрос на микрорынках.
Определить коэффициент R можно следующим образом. На каждом из микрорынков, которые связывает агент, следует иметь данные о приобретении товара у поставщика/продавца и о его реализации покупателю, то есть P1,Q1∈?1 и P2,Q2∈?2. Здесь ?1 и ?2 – области данных, принадлежащие соответственно результатам покупки и продажи товара на микрорынках 1 и 2 (рис. 1). Анализ данных каждой из областей следует направить на выявление закономерностей распределения цены и объемов. В этом случае первое, что обычно приходит в голову – проверка на нормальность распределения случайных величин. Если данный закон распределения подтверждается, найти координату в ?1 и ?2 не составляет особого труда, поскольку речь идет о возможности определения математического ожидания или средней величины. Однако часто анализ указывает на наличие асимметрии (что обусловлено инфляционными процессами), то координаты возможно определить через медиану. Определить коэффициент, связывающий показатели двух микрорынков, можно по выражению
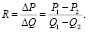 (1)
(1)
Этот коэффициент представляет собой тангенс угла α наклона прямой, связывающий две координаты, каждая из которых относится к своему микрорынку (рис. 1). Величина R может быть как отрицательной (относящейся к спросу), так и положительной (относящейся к предложению). Единицей измерения коэффициента является ден.ед/объем. Для производителей – 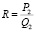 (так как P1,Q1 принимаются равными нулю), конечных потребителей –
(так как P1,Q1 принимаются равными нулю), конечных потребителей – 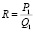 (при P2,Q2 = 0).
(при P2,Q2 = 0).
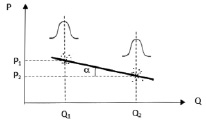
Рис. 1. Линия спроса между микрорынками
Переходя к рассмотрению спроса, сложившегося на микрорынке, построение её линии, которая отвечала бы требования учета практического большинства факторов – сложная задача. Далее будем рассматривать её построение в упрощенной постановке данной задачи.
В простейшем случае линия спроса, определяющая зависимость объема спроса товара от его цены, представляется прямой линией [1, 2], понижающейся с ростом цены:
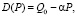 (2)
(2)
где α – модуль тангенса угла наклона линии (что и R) в координатах цена-спрос (P, Q), Q0 – спрос при нулевой цене.
Пример 1. Построение линии спроса линейного вида. Имеется две координаты: (144; 0) и (84; 6). Определим коэффициент: 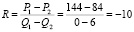 . Функция спроса будет иметь вид:
. Функция спроса будет иметь вид: 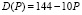 .
.
В действительности спрос D(P) не линеен (одна из его функций представлена в [4]). Когда цена приближается к нулю, объем очень быстро возрастает, а при значительном увеличении цены – медленно стремится к нулю, оставаясь положительным. Если принять во внимание линейную модель спроса (2), то она описывает простейшее приближение линии спроса, достаточно адекватное реальности лишь в окрестности точки рыночного равновесия, когда спрос и предложение сбалансированы. В данном случае если спрос на товар полностью удовлетворен, то выручка от продажи товара (как фактор будущего предложения) определяется по формуле: I = P·D(P).
Важной характеристикой спроса D(P) является следующее: в процессе купли/продажи на микрорынке агенты стремятся обеспечить покупательский спрос и при этом добиться максимальной прибыли путем соответствующего регулирования цены товара. В этом процессе становится очевидным факт того, что слишком высокие цены приведут к снижению покупательского спроса на товар и уменьшат объем продаж с соответствующим понижением прибыли. С другой стороны, попытка установить слишком низкие цены сделает рынок нерентабельным для продавцов. Следовательно, критерий оптимальности поведения микрорынка направлен на соблюдение требования поддержания покупательского спроса при цене, обеспечивающей максимальную прибыль продавцов, т.е. максимальную рентабельность микрорынка. Эти требования не исключают необходимости построения линии спроса для каждого агента, поскольку он, будучи задействованным на микрорынке, определяет спрос. Следовательно, на микрорынке каждый агент на будущее будет придерживаться тактики, опирающейся на собственный спрос, и ему предстоит строить для себя функцию спроса. Тем самым будем иметь к рассмотрению несколько линий спроса. Исходя из сложившейся ситуации на микрорынке в результате купли/продажи сформируется новый спрос с координатами, которые образуют обобщенный спрос. Данный спрос определяет количество благ, которые получат/приобретут все агенты на микрорынке в течение заданного времени и при сложившихся условиях. В такой постановке решение задачи определения координат обобщенного спроса и построения его функции может послужить основанием для принятия к анализу полученных результатов всеми агентами микрорынка. Следовательно, можно рассчитывать на упрощение расчетов распределения товарных потоков в ТПС.
Далее рассмотрим процедуру построения линии спроса нелинейного вида. Как было отмечено выше, наблюдение за спросом – «размазанное» поле точек в пространстве и во времени. Кроме пространственной и временной индивидуальной «размазанности» присутствует коллективная, когда множество факторов распределяются в пространстве, а множество событий – во времени [5]. Анализ коллективного явления предполагает помимо параметров P и Q рассматривать некоторые дополнительные измеримые параметры, которые можно характеризовать некоторой совокупностью распределений. Среди них часто выделяют два класса распределений: экспоненциальное и степенное.
Если имеем в распоряжении данные, относящиеся к рассматриваемым параметрам (не имеющим нулевых значений), то наиболее простой и во многих случаях подтверждающейся гипотезой является гипотеза о том, что параметр (например, Q) имеет нормальное распределение (рис. 1). Аналогично, если анализ указывает на то, что рассматриваемый параметр чаще принимает малые значения, нежели большие, то, вполне возможно, подтвердится гипотеза, когда параметр отвечает экспоненциальному распределению [6].
Тем не менее первое предположение о нормальности распределения считается главной гипотезой [5]. Это связано с тем, что механизм развития нормального распределения выглядит фундаментально просто и элегантно, чего нельзя сказать об упомянутых альтернативах. Простота обеспечивает универсальность механизма, поскольку можем предположить его действие во многих случаях, когда рассматриваемое явление характеризуется параметрами, демонстрирующими колоколообразные распределения.
В подтверждение упомянутого рассмотрим следующий пример. Пусть на микрорынке присутствует несколько агентов (производителей и посредников). Обозначим начальный момент времени, когда агенты не имеют в своем распоряжении ресурсов, то есть количества товаров, подлежащих купле/продаже. Запускаем механизм купли/продажи и под воздействием факторов спроса количество товара случайным образом распределяется между агентами. Очевидно в таком случае будем иметь нормальное распределение и, вполне возможно, с наличием асимметрии. Если аналогичные процессы будут протекать на всех микрорынках, то распределение товарного потока по всей ТПС также будет нормальным. Данное утверждение основано на наличии спроса конечных потребителей, когда товар между ними распределяется случайным образом, в зависимости от их предпочтений.
Еще один пример. Пусть на одном из микрорынков рассматривается вопрос об управлении товарным потоком. В данном случае количество товаров будет попадать на другие микрорынки и по истечении некоторого времени распределение количества товара на них будет экспоненциальным, а не нормальным.
Разница между распределениями товарного потока заключается в том, что в первом примере количество товара на микрорынке связано со спросом (чем чаще возникает спрос, тем больше представлено на рынке товара), тогда как во втором – частота продаж/покупок не зависит от имеющегося количества товара. Очевидно следующее: в первом случае спрос определяет количество реализованного товара, а во втором – скорее всего формируется агентами.
Кроме упомянутых распределений существует особый класс распределений – степенной [7]. В сфере потребления он определяет распределение объема собственных средств граждан некоторого общества. В ситуации, когда гражданин распределяет собственные средства нельзя сказать, что он это делает случайным образом, тем не менее множество граждан определяют спрос на товарном рынке. Не исключено при этом не только нормальное или экспоненциальное, но и степенное распределения, уравнение которого можно записать в таком виде:
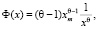 (3)
(3)
где θ > 1 – показатель степени, xm – минимальное значение наблюдаемого статистического параметра x. Поскольку степенное распределение не должно иметь нулевого значения параметра, то необходимо вести нижнюю границу возможных значений параметра, иначе распределение не сходится.
Важное значение в (3) принимает показатель степени. Если принять θ = 2, то будем иметь известный «закон Зипфа» [8, 9]:
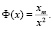 (4)
(4)
Форма данного распределения схожа с формой экспоненциального: малые значения параметра P встречаются чаще (покупатель предпочитает брать больше товара с низкой ценой, нежели с высокой), кривая распределения спадает. Справедливость (4) уместна, когда при покупке товара, покупатель рассчитывает на объем денежных средств C, используя которые он может купить xm по самой высокой цене Pmax. Тогда (4) можно переписать в виде:
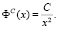 (5)
(5)
Функция (5) имеет степенной вид, то есть относится к степенному закону:
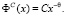 (6)
(6)
Константа C, так же как и θ, имеет фиксированное значение, но может изменяться экспоненциально: 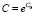 , где C0 – некоторая стартовая величина. Напомним, что степенные распределения наблюдаются в чрезвычайно широком спектре примеров.
, где C0 – некоторая стартовая величина. Напомним, что степенные распределения наблюдаются в чрезвычайно широком спектре примеров.
Построенная кривая спроса (5) на каждом из рассматриваемых участках характеризуется эластичностью. Поскольку нас интересует эластичность по цене, её определяют по формуле:
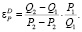 (7)
(7)
Далее представим примеры построения линий спроса, используя функцию (3).
Пример 2. Построение линии спроса вида 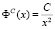 . Условие: имеется одна точка с координатой (144;1) и ряд значений x. Для xm = 1, величина Pmax = 144 является максимальной и определяет величину денежных средств C, необходимых для приобретения товара на микрорынке. Исходные данные и решение представлены в табл. 1.
. Условие: имеется одна точка с координатой (144;1) и ряд значений x. Для xm = 1, величина Pmax = 144 является максимальной и определяет величину денежных средств C, необходимых для приобретения товара на микрорынке. Исходные данные и решение представлены в табл. 1.
Таблица 1
Решение задачи построения
линии спроса 
|
№ п/п |
Количество x (или Q) |
|
|
|
1 |
1 |
144,00 |
– |
|
2 |
2 |
36,00 |
1,3 |
|
3 |
3 |
16,00 |
0,9 |
|
4 |
4 |
9,00 |
0,8 |
|
5 |
5 |
5,76 |
0,7 |
|
6 |
6 |
4,00 |
0,7 |
|
7 |
7 |
2,94 |
0,6 |
Линия спроса изображена на рис. 2.
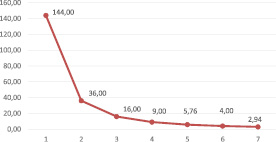
Рис. 2. Линия спроса 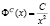
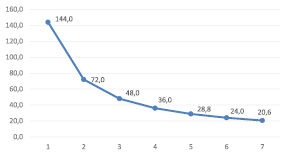
Рис. 3. Линия спроса 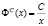
Поскольку спрос по цене в данном примере не эластичен, то есть 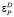 < 1, покупатель готов приобретать больше товара за низкую цену. Однако продавец не всегда готов пойти на такие уступки, поскольку он при продаже старается сопоставить свои доходы с издержками, не планируя при этом понести убытки. По факту, на рис. 2 виден так называемый «тяжелый хвост», указывающий на то, что в области больших значений параметра x спрос спадает гораздо медленнее. Эмпирически это означает, что на микрорынке при экспоненциальном распределении покупки большими партиями при очень низких ценах маловероятны. Следовательно, «тяжелый хвост» степенного распределения содержит в себе эту аномалию. Становится очевидным: возможно, применимо иное экспоненциальное распределение, которое требует подтверждения гипотезы о его существовании. Здесь мы не будем решать данную задачу, а обратимся ко все той же формуле (5), приняв степень θ = 1. В такой постановке задачи, в отличие от предыдущей, следует ожидать положительного результата, в частности роста эластичности спроса по цене.
< 1, покупатель готов приобретать больше товара за низкую цену. Однако продавец не всегда готов пойти на такие уступки, поскольку он при продаже старается сопоставить свои доходы с издержками, не планируя при этом понести убытки. По факту, на рис. 2 виден так называемый «тяжелый хвост», указывающий на то, что в области больших значений параметра x спрос спадает гораздо медленнее. Эмпирически это означает, что на микрорынке при экспоненциальном распределении покупки большими партиями при очень низких ценах маловероятны. Следовательно, «тяжелый хвост» степенного распределения содержит в себе эту аномалию. Становится очевидным: возможно, применимо иное экспоненциальное распределение, которое требует подтверждения гипотезы о его существовании. Здесь мы не будем решать данную задачу, а обратимся ко все той же формуле (5), приняв степень θ = 1. В такой постановке задачи, в отличие от предыдущей, следует ожидать положительного результата, в частности роста эластичности спроса по цене.
Пример 3. Построение линии спроса вида: 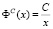 . Условие: наличие координаты (144;1), значений x∈X и Pmax = 144. Исходные данные и решение представлены в табл. 2.
. Условие: наличие координаты (144;1), значений x∈X и Pmax = 144. Исходные данные и решение представлены в табл. 2.
Таблица 2
Решение задачи построения
линии спроса 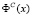
|
№ п/п |
Количество x (или Q) |
|
|
|
1 |
1 |
144,00 |
– |
|
2 |
2 |
72,0 |
2,0 |
|
3 |
3 |
48,0 |
1,5 |
|
4 |
4 |
36,0 |
1,3 |
|
5 |
5 |
28,8 |
1,3 |
|
6 |
6 |
24,0 |
1,2 |
|
7 |
7 |
20,6 |
1,2 |
Линия спроса изображена на рис. 3.
Как видно, на рис. 3 «тяжелый хвост» отсутствует. Спрос по цене в данном примере эластичен, 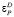 > 1, что в целом при равных обстоятельствах, складывающихся на микрорынке, оправдывает предположение о наличии в рассматриваемой функции величины θ = 1.
> 1, что в целом при равных обстоятельствах, складывающихся на микрорынке, оправдывает предположение о наличии в рассматриваемой функции величины θ = 1.
В конечном итоге нельзя однозначно сказать о том, какой вид будет иметь линия спроса, которая необходима агенту как некоторое условие для совершения сделок покупки/продажи. Для более точного результата все-таки требуется выполнить процедуру обработки статистических данных с тем, чтобы подтвердить гипотезу о наличии закона распределения случайной величины.
Заключение
Построение линии потребительского спроса для агентов торгово-посреднической сети предполагает наличие математической модели, а по существу – функции спроса. Она позволяет агенту торгово-посреднической сети определиться с ценой и объемами продаж/покупки на её микрорынках. Построение функции спроса основывается на наличии статистических данных параметров рынка (цена и объем продаж) и их обработке. Выдвигая гипотезу о возможном распределении случайной величины рассматриваемого параметра, её подтверждение – основа для построения функции спроса. В тех случаях, когда рынок нестабилен, довольно сложно решить задачу о справедливости наличия закона распределения случайной величины. Здесь прослеживается вариант, когда с некоторой долей уверенности, при наличии одной или двух координат на евклидовом пространстве (имеющих некоторое усредненное или медианное значение), можно построить функции спроса в виде прямой или кривой линии.
Представленная в данной работе математическая модель построения линий спроса, в своей основе базируется на уравнении степенного распределения. Выдвигается подтверждённое примерами предположение о том, что степень определяет не только связь цены с объемом, но и обосновывает взаимоотношения агентов на микрорынке торгово-посреднической сети, пусть даже и в весьма упрощенной постановке задачи. Изменяя степень и начальные условия, модель позволяет строить линию спроса с её приближением к реально складывающемуся спросу на микрорынке.
Исследование выполнено при финансовой поддержке РФФИ и республики Хакассия в рамках научного проекта № 19-47-190001.