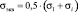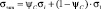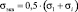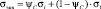Данная публикация является продолжением исследований, проводимых авторами и опубликованных ранее в диссертациях [1, 2], а позже в статьях [3, 4]. Одной из наиболее сложных проблем в расчётах на длительную прочность является определение значений эквивалентных напряжений [5], на основе которых рассчитывается время до разрушения конструкции. Для таких расчётов наиболее универсальным и обоснованным, по мнению авторов, является обобщённый критерий длительной прочности Писаренко – Лебедева [6].
В предыдущей публикации [4] авторами был предложен достаточно простой и удобный способ конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева, применяемого при определении эквивалентных напряжений, используемых для описания процессов накопления повреждений в материале с помощью кинетического уравнения повреждаемости Ю.Н. Работнова [7]. При этом параметр, характеризующий «степень ответственности сдвиговой деформации за микроразрушение, создающий благоприятные условия для растрескивания и разрушения материала» [6], считается равным относительному остаточному сужению при разрыве стандартного образца, значение которого можно определить по информации, имеющейся в справочной литературе для большинства конструкционных материалов. В работах [3] и [4] был проведен анализ экспериментальных данных, который показал, что такой подход обеспечивает возможность вычисления эквивалентного напряжения с достаточной степенью достоверности. Кроме этого, с использованием обобщенного критерия длительной прочности Писаренко – Лебедева и предложенного способа его конкретизации был проведен расчет напряженно-деформированного состояния плоской пластины с отверстием [4].
Однако для того, чтобы сделать окончательный вывод о возможности использования предложенного способа конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева, требуется сравнение результатов расчетов, полученных с помощью рассмотренного критерия длительной прочности, с результатами натурных экспериментов. Только в случае хорошего согласования результатов расчетов и экспериментов можно считать предложенный способ конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева достаточно обоснованным [8].
Цель исследования: выполнение проверочных численных расчетов времени до разрушения ряда простых осесимметричных конструкций (к которым, в частности, относятся кольцевые пластины и трубы), для которых имеются экспериментальные значения времени разрушения. На основе сравнения полученных результатов планируется сделать вывод о достоверности предложенного способа конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева, предложенного ранее авторами в публикации [4].
Материалы и методы исследования
Для определения эквивалентного напряжения при помощи обобщенного критерия длительной прочности Писаренко – Лебедева используется следующее соотношение [6]:
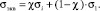(1)
Здесь σэкв – эквивалентное напряжение; χ – коэффициент пластичности материала, характеризующий степень ответственности сдвиговой деформации за макроразрушение, σi – интенсивность напряжений, которая в случае плоского напряженного состояния будет определяться с помощью следующей формулы: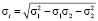 
, σ1 и σ2 – главные нормальные напряжения.
Для конкретизации указанного критерия требуется определить значение величины χ. В работе [4] достаточно подробно описаны варианты определения данного параметра при различных видах нагружения. Там же был предложен простой и удобный для использования в практических расчётах способ определения этого параметра. Суть его заключается в том, что параметр χ для материала принимается численно равным относительному остаточному сужению ψC сплошного круглого образца, полученному при его испытании на ползучесть и длительную прочность при постоянном напряжении σ и заданной фиксированной температуре Т.
Возможность использования такого подхода обусловлена многочисленными результатами практических испытаний стандартных цилиндрических образцов, изготовленных из металлов и сплавов на ползучесть и длительную прочность, проведенных в разные годы, например, таких как [9].
Тщательный анализ этих результатов позволил выявить следующую закономерность [1, 10]: при высоких уровнях напряжений, значительно превышающих предел текучести материала, преобладает внутризеренное (вязкое) разрушение, которое сопровождается локализацией деформаций ползучести и последующим образованием характерной шейки [11]. Относительное остаточное сужение образца ψC, полученное при испытаниях на ползучесть, почти равно относительному остаточному сужению ψ, полученному при стандартном испытании на растяжение цилиндрических образцов при той же температуре.
Вместе с тем, если значение действующих напряжений незначительно превышает предел ползучести материала и значительно ниже предела текучести, в основном преобладает межзеренный характер деформации, имеет место охрупчивание материала без образования шейки, то есть деформация образца в течение всего процесса нагружения практически постоянна по всей длине [12, 13].
Величина накопленной необратимой деформации в таких условиях, наоборот, будет малой, а время до разрушения – большим, порядка тысяч, а в отдельных случаях – десятков тысяч часов. В этих условиях величина относительного остаточного сужения ψC будет стремиться к нулю, а разрушение материала будет иметь хрупкий характер. В условиях эксплуатации реальных конструкций это представляет серьезную опасность, поскольку материал разрушается внезапно и без видимых деформаций.
Опираясь на результаты, изложенные выше, авторами была построена зависимость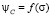 
для фиксированных значений температуры следующего вида [4]:
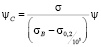, (2)
где ψC – относительное остаточное сужение стандартного образца круглого сечения, получаемое при испытании на ползучесть и длительную прочность при постоянном напряжении σ и фиксированной температуре Т; ψ – относительное остаточное сужение, полученное при испытании на разрыв (при мгновенной деформации) стандартного образца круглого сечения при его и при такой же температуре; σВ – предел прочности материала;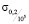 
– предел ползучести материала при указанной температуре.
Таким образом, в рамках рассмотренного здесь подхода вычисление эквивалентного напряжения для каждого элемента конструкции производится с использованием следующей формулы:
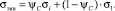(3)
Величина ψC вычисляется по формуле (2). Исходные данные, необходимые для выполнения расчетов, дополняются следующими механическими свойствами материала, определяемыми при фиксированной температуре в пределах диапазона ее изменения в процессе эксплуатации конструкции: предел прочности, предел ползучести и относительное остаточное сужение. Эти данные имеются в справочной литературе для большинства конструкционных материалов [14, 15].
В работе [4] был проведен анализ результатов моделирования, полученных с использованием предложенного подхода, который показал, что выбор критерия длительной прочности оказывает влияние на оценку расчетного времени до разрушения конструкции существенным образом, и это влияние тем больше, чем меньше нагрузка и больше время нагружения конструкции. Предложенный вариант конкретизации обобщенного критерия Писаренко – Лебедева позволяет учитывать изменение пластических характеристик материала (охрупчивание), возникающее при развитии деформаций ползучести.
Следующим этапом исследований является проверка достоверности результатов прочностного расчета конструкций, получаемых с использованием обобщенного критерия Писаренко – Лебедева.
К настоящему времени опубликовано большое количество работ, посвященных экспериментальным и теоретическим методам изучения накопления повреждений в кристаллических телах и их разрушению. Примерами могут служить некоторые работы, приведенные в обзоре [9]. Однако в основном эти работы посвящены исследованию повреждаемости цилиндрических образцов или других изделий с простой геометрической формой. Однако для проведения полноценной проверки достоверности предложенного способа конкретизации критерия длительной прочности требуются результаты натурных экспериментов по исследованию ползучести и разрушения изделий, выполненных в виде тонких оболочек вращения.
К сожалению, в настоящее время такие эксперименты практически не проводятся, как в России, так и в мире. Поэтому авторами были взяты за основу результаты экспериментов, опубликованных в предыдущие годы, такие как [16, 17]. Далее рассмотрим эти эксперименты более подробно.
Результаты исследования и их обсуждение
В рамках данной работы будут рассмотрены результаты двух натурных экспериментов – цилиндрическая оболочка, находящаяся под действием внутреннего давления и тонкая пластинка с круглым отверстием, растягиваемая внешними радиальными силами. Для каждого из экспериментов имеются данные о времени разрушения, а также значения деформаций конструкций в определенные моменты времени.
В рассматриваемом примере путем сопоставления результатов расчета и эксперимента оценивается достоверность определения, с помощью разработанной методики, времени разрушения оболочек, находящихся в условиях неустановившейся ползучести.
В качестве материала в обеих задачах была взята сталь 20, механические характеристики которой, необходимые для решения рассматриваемых задач, взяты из справочной литературы [14, 15]. Эти характеристики использовались авторами ранее при расчетах других конструкций.
В данной статье будут рассмотрены только результаты расчетов времени до разрушения конструкций и их соответствие результатам экспериментов. Анализ кинетики разрушения конструкций, развитие деформаций и накопление повреждений этих конструкций будут проанализированы авторами позже в других публикациях.
Расчет обеих конструкций проводился с использованием четырех различных критериев длительной прочности:
– максимальное главное напряжение (критерий Джонсона): σэкв = σ1;
– интенсивность напряжений (критерий Каца): σэкв = σi;
– критерий Сдобырева: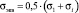 
;
– обобщённый критерий Писаренко – Лебедева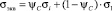 
.
Расчеты с применением первых трех критериев были проведены авторами ранее в работах [3] и [4].
Минимальная оценка времени разрушения конструкции (абсолютно хрупкое разрушение) возможна при использовании критерия Джонсона, а максимальная (абсолютно пластическое разрушение) – при использовании критерия Каца [3, 4]. Это означает, что независимо от того, какой критерий длительной прочности применяется, время до разрушения элемента конструкции всегда будет находиться в диапазоне между значениями, полученными при использовании критериев Каца и Джонсона. Критерий Сдобырева – это их полусумма, таким образом, вклад вязкого и хрупкого характеров разрушений в общую картину должен быть равнозначным.
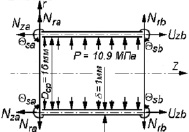
Рис. 1. Ползучесть и разрушение цилиндрической оболочки под действием внутреннего давления (эксперимент Ш.Н. Каца)
В данном эксперименте был исследован процесс ползучести и разрушения тонкой цилиндрической оболочки при действии на нее постоянного внутреннего давления (рис. 1). Данный эксперимент был проведен в 1955 г. ученым Ш.Н. Кацем [16] с целью обоснования предложенного им критерия длительной прочности. Торцы рассматриваемой оболочки заглушены донышками, вследствие чего в ее элементах, помимо окружных, возникают и меридиональные напряжения. Исходные данные, заложенные в условие задачи, соответствуют условиям эксперимента, выполненного на тонкостенном образце из материала, имеющего аналогичные стали 20 основные механические характеристики. Образец испытывался при постоянной температуре Т = 500 °С и постоянном внутреннем давлении Р = 10,9 МПа и имел следующие геометрические размеры: средний диаметр 3,57 см; толщину стенки 0,17 см.
В табл. 1 приведены экспериментальные и расчетные значения времени разрушения исследуемой конструкции, полученные с использованием четырех различных критериев длительной прочности.
Таблица 1
|
Эксперимент |
Результаты расчетов с использованием следующих критериев |
||||
|
σэкв = σ1 |
σэкв = σi |
|
|
||
|
Время разрушения образца (час) |
1176 |
1112 |
2785 |
1732 |
1154 |
|
Погрешность, % |
5,5 |
137 |
47 |
1,8 |
|
Как видно из табл. 1, использование в расчете в качестве критерия длительной прочности значений наибольшего главного напряжения позволило определить время разрушения оболочки с достаточно малой, по сравнению с экспериментом, погрешностью 5,5 %. В то время как использование критериев Сдобырева и интенсивности напряжения дает завышенные, соответственно на 47 % и 137 %, значения долговечности образца, что совершенно неприемлемо.
Использование обобщённого критерия длительной прочности Писаренко – Лебедева позволяет получить результат, наиболее близкий к экспериментальному.
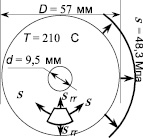
Рис. 2. Ползучесть и разрушение тонкой пластинки с круглым отверстием (эксперимент Д. Хейхерста)
В данной задаче была исследована кинетика изменения напряженно-деформированного состояния и процесса разрушения, вследствие ползучести, тонкой круглой пластинки диаметром 5,7 см с центральным круговым отверстием диаметром 0,95 см (рис. 2). Пластинка при постоянной температуре Т = 500 °С подвергается длительному, всестороннему растяжению нагрузкой интенсивностью 48,3 МПа. Эксперимент, результаты которого приведены в работе [17], выполнялся на специально спроектированной установке и специальных образцах крестообразной формы. Конструкции испытательной установки и испытуемого образца обеспечивали возникновение в центральной части образца равномерно нагруженного участка радиусом 57 мм. Это позволило рассматриваемую задачу решать в осесимметричной постановке.
В ходе вычислительного эксперимента было установлено, что уровень напряжений в элементах пластинки в течение всего процесса ее нагружения остается существенно ниже предела текучести материала 150 МПа. Это указывает на преобладание хрупкого характера разрушения над вязким.
Как видно из табл. 2, использование в расчете в качестве значений напряжения позволило определить время полного разрушения пластинки с достаточно малой по сравнению с экспериментом погрешностью 15 %. Использование же в расчетах критериев и привело к значительному (соответственно в 2,7 раза и 1,5 раза) завышению расчетной долговечности пластинки. Также можно сделать вывод, что полученные результаты подтверждают достоверность обобщённого критерия длительной прочности Писаренко – Лебедева и предложенного способа его конкретизации.
Таблица 2
|
Эксперимент |
Результаты расчетов с использованием следующих критериев |
||||
|
σэкв = σ1 |
σэкв = σi |
|
|
||
|
Время разрушения образца (час) |
410 |
348 |
1118 |
602 |
397 |
|
Погрешность, % |
15,1 |
172,7 |
46,8 |
3,1 |
|
В результате проведенных исследований авторами установлено, что использование в расчетах критериев длительной прочности, не соответствующих преобладающим механизмам разрушения, может привести к существенным погрешностям при определении времени разрушения оболочек.
Заключение
Таким образом, в ходе проведенных исследований была подтверждена адекватность предложенного способа конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева. Полученные результаты расчетов имеют хорошее согласование с аналогичными экспериментальными результатами. Следовательно, предложенный способ конкретизации обобщенного критерия длительной прочности Писаренко – Лебедева, по мнению авторов, обеспечивает получение наиболее точных результатов расчетов, по сравнению с другими широко применяемыми критериями длительной прочности. Однако в настоящей статье рассмотрено всего два варианта конструкций и способа их нагружения и один материал. Поэтому утверждать об универсальности рассмотренного критерия длительной прочности только на основании представленных результатов нельзя. В дальнейшем авторы планируют продолжить исследования.
Авторы также будут признательны всем специалистам, выполняющим аналогичные прочностные расчеты конструкций, за любые конструктивные замечания и рекомендации.