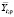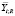Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

В настоящее время вопросы, связанные с тепловой защитой зданий и сооружений, являются важнейшими направлениями строительной отрасли. Наибольший практический интерес с точки зрения экономии тепловой энергии представляют ограждающие конструкции, которые непосредственно контактируют с внешней средой. По данным многих исследователей, через ограждающие конструкции теряется порядка 70–85 % тепловой энергии [1]. В связи с этим актуальной задачей является проектирование и расширение номенклатуры теплоизоляционных и конструкционно-теплоизоляционных стеновых материалов и изделий с использованием высокоэффективных сырьевых компонентов. Наиболее практическим решением рассмотренной задачи является применение пористых гранулированных материалов в качестве крупного заполнителя в бетонах [2].

По требованиям ГОСТ 25192-2012, к категории легких бетонов относятся бетоны, у которых марка по средней плотности варьируется от D800 до D2000. А бетоны, имеющие марку по средней плотности менее D800, называют особо легкими. Тем не менее под обобщающим термином легкие бетоны принято называть все виды бетонов с использованием пористых заполнителей (независимо от марки по средней плотности). Преимущества легких бетонов на пористых заполнителях были отражены в фундаментальных работах Ю.М. Баженова, Г.И. Горчакова и А.Г. Комара. Теоретические и экспериментальные исследования по легким бетонам, охватывающих ряд вопросов, связанных с решением системы «состав – структура – свойства», также проводились и другими авторами [3, 4].

С точки зрения технологии изготовления, большинство разновидностей легких бетонов имеют некоторые специфические отличия от тяжелых и мелкозернистых бетонов. Прежде всего, эти отличия заключаются в свойствах пористых заполнителей и в особенностях их взаимодействия в процессе структурообразования и твердения растворной составляющей.

Следует отметить, что большинство современных подходов к проектированию составов легких бетонов отрабатывались в первую очередь на примере керамзитобетона [5]. Тем не менее ограниченность качественного глинистого сырья с высоким коэффициентом вспучивания ставит вопрос о замене керамзита на более эффективный материал, обладающий высокими механическими и теплофизическими характеристиками. Одним из таких материалов является гранулированное пеностекло [6]. Благодаря высокой пористости зерен, на основе гранулированного пеностекла можно получить легкие бетоны с пониженной средней плотностью без существенных потерь прочностных характеристик.

Проектирование состава теплоизоляционного и конструкционно-теплоизоляционного легкого бетона зачастую проводится опытным путем. Наиболее применимым из опытно-экспериментальных методов анализа является аппарат теории математического планирования эксперимента [7]. Данный метод широко распространен в инженерной практике благодаря значительному сокращению количества опытов, а также возможностью проведения вычислительных экспериментов.

Цель исследования: оценка возможности применения метода математического планирования эксперимента в проектировании составов легкого бетона на основе гранулированного пеностекла.

Материалы и методы исследования

В работе были использованы следующие сырьевые компоненты: портландцемент марки ЦЕМ I 32,5Б по ГОСТ 31108-2016 производства АО «Якутцемент» (минералогический состав, %: C3S – 58,7; C2S – 16,38; C3A – 6,44; C4AF – 14,35); гранулированное пеностекло по ТУ 5914-001-00643867-94 производства НПО «Силикат» (химический состав, %: SiO2 – 66,3; Na2O – 19,1; СаО – 6,65; MgO – 5,54; Al2O3 – 1,2; др. – 1,21); техническая вода по ГОСТ 23732-2011.

Определение основных физико-механических показателей гранулированного пеностекла проведено в соответствии с требованиями ГОСТ 9758-2012. Испытания образцов легкого бетона выполнены с использованием стандартных методов, аттестованных приборов и оборудования. Подбор состава легкого бетона рассчитан в соответствии с требованиями, изложенными в ГОСТ 27006-86. В экспериментальных исследованиях использованы стандартные образцы-кубы размером 10х10х10 см по ГОСТ 10180-2012. Статистическая обработка экспериментальных данных проведена с учетом положений ГОСТ Р ИСО 16269-4-2017 на базе программы MathCAD 2001i.

Результаты исследования и их обсуждение

На основании положений, рассмотренных в работах [3, 8, 9], в качестве выходных данных выбраны средняя плотность ρ₀ и прочность при сжатии Rсж. Для достижения максимально плотной упаковки зерен в композите, гранулированное пеностекло условно разделили на две фракции, «крупную» и «мелкую». Гранулы «крупной» фракции имеют диаметр частиц 5–7,5 мм, мелкой фракции 2,5–5 мм соответственно. По данным работы [3] и собственных исследований [6], в качестве рецептурных факторов установили расход цемента X1 и водоцементное отношение X2. В табл. 1 показаны уровни и шаг варьирования факторов.

Таблица 1

Уровни и шаг варьирования факторов

С учетом параметров, приведенных в табл. 1, составлен план двухфакторного эксперимента с тремя уровнями варьирования. Составлены девять опытов, состоящих из двух параллельных экспериментов. После формования образцы твердели и набирали прочность в камере нормального твердения при температуре 20 ± 2 °С и относительной влажности воздуха 95 ± 5 %. При достижении 28 суток с момента изготовления у образцов определены средняя плотность и предел прочности при сжатии. План и результаты полного факторного эксперимента приведены в табл. 2. Индекс i показывает порядковый номер опыта, варьируется от 1 до 9. 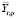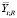Выходные параметры и являются среднеарифметическими значениями двух параллельных экспериментов Y1;i и Y2;i.

Таблица 2

План и результаты полнофакторного эксперимента

Экспериментальные данные использованы для разработки математической модели, которая представляет собой функцию отклика, связывающую факторы X1 и X2 с параметрами выходных данных. В данном случае функция отклика выражается полиномом второй степени [8]:

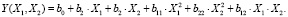(1)

Расчет коэффициентов уравнения регрессии b0, b1, b2, b11, b22 и b12 производится по следующим формулам [8]:

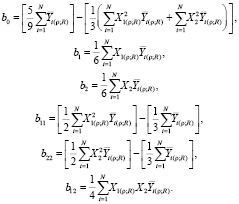(2)

По формулам (2) рассчитаны по шесть коэффициентов регрессии для каждого из двух полиномов. Значения вычисленных коэффициентов регрессии приведены в табл. 3 (полужирным шрифтом в табл. 3 отмечены незначимые коэффициенты регрессии).

Таблица 3

Коэффициенты уравнений регрессии

Следующим этапом анализа является оценка значимости коэффициентов регрессии. Для этого по результатам параллельных опытов (табл. 2 столбцы № 4–9) рассчитывается дисперсия воспроизводимости. Данный показатель необходим для статистического анализа результатов эксперимента. При дублировании опытов по строкам плана, дисперсия воспроизводимости определяется по следующей формуле [10]:

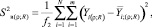(3)

где f2 = N(m – 1) – число степеней свободы;

N – количество опытов;

m – количество параллельных опытов.

Значимость коэффициентов регрессии оценивается по критерию Стьюдента. При уровне значимости α = 0,05 и для числа степеней свободы f2 = N(m – 1) = 9(2 – 1) = 9, табличное значение критерия Стьюдента составляет tкр = 2,26 [10]. Доверительный интервал, соответствующий вероятности р = 0,95, определяется через среднюю дисперсию параллельных опытов с учетом табличного значения критерия Стьюдента по формуле [11]:

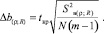(4)

Проверяется значимость коэффициентов на выполнение условия [10]:

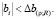(5)

По результатам оценки значимости оказалось, что из всех данных незначимыми коэффициентами оказались b22 и b12 (табл. 3). Окончательный вид полиномов после исключения незначимых коэффициентов имеет вид

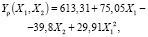(6)

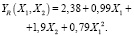(7)

Сумма квадратов разностей между рассчитанными и экспериментальными значениями позволяет вычислить дисперсию адекватности модели по формуле [12]:

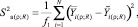(8)

где f1 – число степеней свободы, f1 = N – k, k – количество коэффициентов полинома; 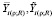– экспериментальное и рассчитанное значение выходных данных в i-м опыте.

Дисперсия адекватности определяет степень отклонения экспериментальных и рассчитанных данных, а также позволяет оценить работоспособность полученного полинома. Наблюдаемое значение критерия Фишера определяется по соотношению [10–12]:

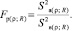(9)

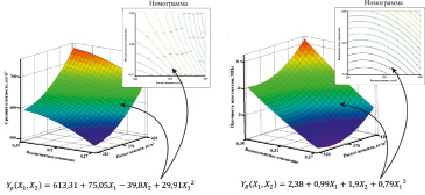
а) б)

Зависимость средней плотности (а) и прочности при сжатии (б) от расхода цемента и водоцементного отношения

Далее, проверяется следующее условие [10–12]:

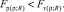(10)

Критическое значение критерия Фишера при уровне значимости α = 0,05 для выходных параметров Yρ и YR составляет Fт;(ρ;R) = 3,48 (f1 = 5, f2 = 9) [12]. Сравнивая наблюдаемые и критические значения критерия Фишера по условию (10), можно сделать вывод, что:

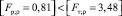– условие выполняется;

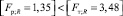– условие выполняется.

Следовательно, полиномы (6) и (7) при уровне значимости α = 0,05 являются адекватными экспериментальным данным и пригодными для дальнейшего анализа.

По полиномам (6) и (7) построены поверхности отклика и номограммы зависимости средней плотности и прочности при сжатии от расхода цемента и водоцементного отношения (рисунок). Рисунок представляет собой графическую интерпретацию полиномов (6) и (7).

На основании полученных зависимостей (рисунок) можно сделать вывод, что наиболее сильное влияние на изменение средней плотности оказывает расход цемента (X1). Ввиду достаточно значительной разности плотностей цементного камня и гранулированного пеностекла, данный эффект является вполне очевидным. Выявлен отрицательный линейный эффект водоцементного отношения (X2 = –39,8) на плотность композита. Это объясняется повышением пористости цементного камня при повышении его водосодержания, что в последующем приводит к снижению плотности материала. Установлен положительный эффект изменения прочности легкого бетона при повышении содержания цемента (X1 = + 0,99) и водоцементного отношения (X2 = + 1,9). Как и большинство бетонов гидратационного твердения, увеличение содержания вяжущего благоприятно влияет на формирование прочностных характеристик материала. Однако самый весомый вклад в формирование прочности оказывает водоцементное отношение. В эксперименте водоцементное отношение варьируется от 0,27 до 0,35. При минимальных значениях водоцементного отношения наблюдается резкое снижение прочности при сжатии. Это связано, во-первых, с нехваткой воды затворения для обеспечения реакции гидратации, во-вторых, миграцией части воды в поверхностные слои гранул пеностекла. Минимальная плотность и прочность наблюдаются при расходе цемента 320 кг/м3 и водоцементном отношении 0,27. Максимальная плотность и прочность выявлены при расходе цемента 420 кг/м3 и водоцементном отношении 0,35. Совместные влияния факторов на изменения выходных данных не обнаружены. В целом особенности изменения поверхностей отклика (Yρ и Y_R) имеют практически одинаковое направление, а также идентичные причинно-следственные связи с входными факторами (X1 и X2).

По разработанным составам легкого бетона получен конструкционно-теплоизоляционный стеновой материал, соответствующий требованиям ГОСТ 25820-2014, марки по средней плотности D500-D700, класса по прочности при сжатии В0,5-В3,5 и теплопроводностью (в сухом состоянии) 0,121–0,137 Вт/(м·К).

Таким образом, использование метода математического планирования эксперимента позволяет проектировать и получать легкий бетон с достаточно широким диапазоном изменения средней плотности и прочности при сжатии.

Заключение

На основании проведенного исследования обоснована целесообразность применения метода математического планирования эксперимента при проектировании составов конструкционно-теплоизоляционного легкого бетона с пористым заполнителем из гранулированного пеностекла. Отличительной особенностью данного метода от известных методов численного анализа является возможность получения нескольких возможных решений поставленной задачи. То есть, сочетая значения входных факторов друг относительно друга, можно получить огромное количество выходных данных (в области определения функции) не прибегая к лабораторным испытаниям. Такой подход позволяет получить максимально возможное количество информации об изучаемом объекте с заданной степенью точности прогноза при минимальных затратах ресурсов и времени.