Для обеспечения эффективной работы в различных условиях низкоорбитальные системы спутниковой связи (НССС) должны обладать свойством помехозащищенности. Согласно [1] обеспечить помехозащищенность возможно за счет решения проблемы придания НССС информационной, структурной и энергетической скрытностей. Так как от информационной скрытности во многом зависит помехозащищенность группировки низкоорбитальных космических аппаратов, то разработка методов ее повышения является актуальной задачей. В работах [2, 3] для повышения информационной скрытности НССС предлагается использовать систему, позволяющую аутентифицировать спутник перед началом сеанса связи. При использовании такой системы спутник-нарушитель не сможет навязать необслуживаемому объекту управления ретрансляционную помеху, имитирующую команду управления.
Дальнейшее повышение информационной скрытности НССС возможно за счет использования шифрования. Применение шифрования не позволяет злоумышленнику при перехвате передаваемых данных понять их смысл [4, 5]. В основу нелинейных методов шифрования положены арифметические операции, выполняемые по модулю большого простого числа М. Применение комбинаций мультипликативных и аддитивных операций позволяет повысить криптостойкость зашифрованного текста, а также устранить уязвимости поточных шифров, использующих в качестве ключевой гаммы псевдослучайные последовательности. Однако использование одномодульного принципа построения таких методов шифрования не позволяет обеспечить высокую скорость зашифрования. Устранить данный недостаток можно за счет применения модулярных кодов (МК), которые позволяют проводить арифметические операции параллельно, используя данные малой разрядности. Поэтому разработка метода нелинейного шифрования данных на основе возведения в степень по модулю с использованием МК является актуальной задачей.
Современные системы нелинейного шифрования применяют арифметические операции, выполняемые в кольце большого целого числа М. Известно, что скорость выполнения операции возведения в степень по модулю обратно пропорциональна разрядности числа М. Однако для обеспечения высокой криптостойкости выбирают числа, разрядность которых находится в пределах от 140 до 512 бит [6]. Повысить скорость выполнения процедуры шифрования без снижения криптостойкости можно за счет использования модулярных кодов. Поэтому целью работы является снижение временных затрат на выполнение операции возведения в степень по модулю, используемой в нелинейных шифрах, за счет использования модулярных кодов.
Материалы и методы исследования
Среди методов шифрования особое место отводится методам нелинейного шифрования. Следует отметить, что данные методы закрытия позволяют устранить уязвимости поточных систем шифрования, в которых в качестве ключевой гаммы используются псевдослучайные последовательности [6, 7]. Это связано с тем, что методы нелинейного шифрования используют модульные операции модульного сложения и умножения. При этом в качестве модуля берется большое простое число М. Представить данное число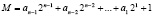 
, в виде полиномиальной формы вида
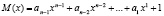. (1)
Аналогичным образом поступим с открытым текстом и ключевыми данными. Получаем
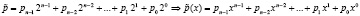, (2)
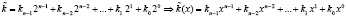, (3)
где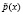 
– n-разрядный открытый блок, представленный в виде полинома; 
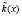– n-разрядный блок секретного ключа, представленный в виде полинома.
Тогда методы нелинейного шифрования можно представить в виде
, 
, 
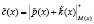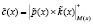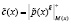. (4)
где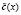 
– n-разрядный зашифрованный блок-полином; 
.
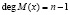Рассмотрим метод нелинейного шифрования, использующий операцию возведения в степень по модулю. Известно, что данный метод обладает высокой криптостойкостью по сравнению с аддитивными и мультипликативными операциями, представленными выше. Поэтому в статье будет рассмотрен данный метод и способ, позволяющий повысить скорость выполнения процедуры шифрования.
Для выполнения процедуры расшифрования используется выражение
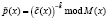. (5)
Известно, что для выполнения операции возведения в степень по модулю необходимо выполнить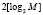 
операций умножения. Очевидно, что при больших значениях простого числа М увеличиваются временные затраты на операцию зашифрования и расшифрования.
Одним из эффективных способов решения выявленной проблемы является использование модулярных кодов, в которых в качестве оснований выступает набор взаимно простых полиномов μi(x), где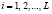 
, для которых справедливо 
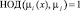, при условии 
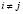. Количество модулей μi(x) выбирается из условия
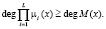(6)
Таким образом, одномерная операция возведения в степень по модулю M(x) сводится к L аналогичным операциям, выполняемым параллельно с использованием модулярного кода. Тогда процедура зашифрования представляется выражением
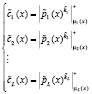. (7)
где
;
; 
.
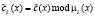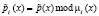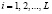Используя изоморфизм китайской теоремы об остатках, реализуем операцию расшифрования с использованием модулярных кодов согласно
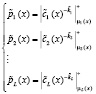. (8)
Использование модулярного полиномиального кода позволяет отказаться от операций прямого преобразования (позиционный код – модулярный код) и обратного преобразования из модулярного в позиционный код. В этом случае получаем
;
; 
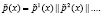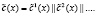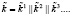(9)
Анализ выражений (7) и (8) показывает, что реализация метода нелинейного шифрования в кольце полиномов позволит повысить скорость выполнения процедур зашифрования и расшифрования. Пусть максимальная степень выбранного основания модулярного полиномиального кода равна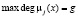 
, тогда для процедуры зашифрования одного блока открытого текста необходимо выполнить не более 
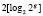операций умножений. Так как набор выбранных оснований модульного кода должен удовлетворять условию (6), то имеем, что g < (n – 1). Это означает, что применение модулярных кодов при выполнении операции возведения в степень по модулю позволяет повысить скорость выполнения нелинейного шифрования.
Результаты исследования и их обсуждение
Рассмотрим пример реализации метода нелинейного шифрования данных на основе возведения в степень по модулю с использованием МК. В качестве оснований модулярного кода используем μ1(х) = x5 + x3 + x2 + x + 1; μ2(х) = x5 + x4 + x3 + x + 1; μ2(х) = x5 + x4 + x3 + x2 + 1. Таким образом, получаем, что выбранные основания позволяют заменить модуль М, степень которого составляет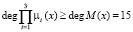 
.
Рассмотрим входной поток открытых символов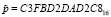 
. Секретный ключ задается генератором ключевой гаммы и имеет вид 
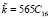. Так как 
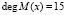, то входная последовательность разбивается на блоки по 15 бит каждый. Затем каждый такой блок представляет собой конкатенацию трех пятибитовых подблоков. Каждый из таких подблоков представляет собой остаток по основаниям МК. Затем эти подблоки возводятся в степень по модулям μi(x), где i = 1, 2, 3.
При заданном потоке открытых данных первый 15-разрядный блок данных имеет вид
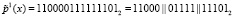. Каждый из подблоков, длиной 5 бит открытых данных, представляет собой остаток по модулю μi(x), где i = 1, 2, 3. Тогда получаем полиномы 
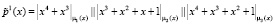. Блок ключевой гаммы разделим на подблоки по 5 бит каждый. Первый подблок имеет вид 
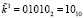. Воспользуемся выражением (7) и зашифруем первый блок данных:
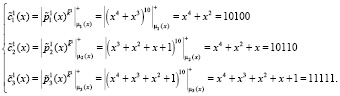
Тогда первый блок зашифрованного текста равен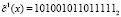 
.
Второй 15-разрядный блок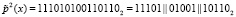 
. Так как каждый из подблоков представляет собой остаток по модулю μi(x), где i = 1, 2, 3, то 
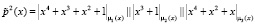. Второй подблок ключевой гаммы имеет вид 
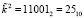. Зашифруем второй блок данных с помощью МК:
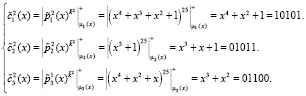
Тогда второй блок зашифрованного текста равен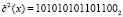 
.
Третий 15-разрядный блок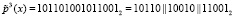 
. Так как каждый из подблоков представляет собой остаток по модулю μi(x), где i = 1, 2, 3, то получаем полиномы 
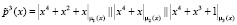. Третий подблок ключевой гаммы 
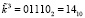. Зашифруем третий блок данных с помощью МК:
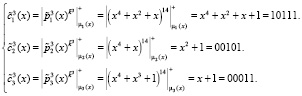
Тогда третий блок зашифрованного текста равен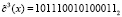 
.
Выполним расшифрование с использованием разработанного метода нелинейного шифрования данных на основе возведения в степень по модулю с использованием МК. Для этого необходимо произвести вычисление секретного ключа, используемого на приемной стороне. Учитывая особенности реализации мультипликативных операций с использованием выбранных полиномов, получаем, что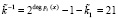 
. Для второго блока ключевой гаммы получаем 
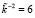, а для третьего – 
.
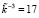При заданном потоке зашифрованных данных первый 15-разрядный блок данных имеет вид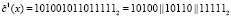 
. Каждый из подблоков, длиной 5 бит зашифрованных данных, представляет собой остаток по модулю μi(x), где i = 1, 2, 3. Тогда получаем 
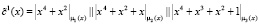. Первый подблок ключевой гаммы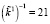 
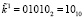. Воспользуемся выражением (8) для расшифрования первого блока закрытых данных:
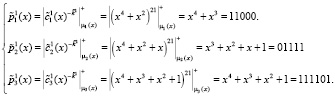
Тогда первый блок расшифрованного текста равен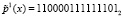 
.
Второй 15-разрядный блок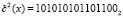 
. Так как каждый из подблоков представляет собой остаток по модулю μi(x), где i = 1, 2, 3, то 
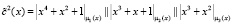. Второй подблок ключевой гаммы имеет вид 
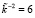. Расшифруем второй блок данных с помощью МК:
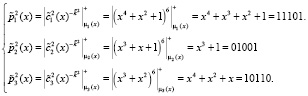
Тогда второй блок расшифрованного текста равен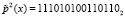 
.
Третий 15-разрядный блок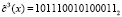 
. Так как каждый из подблоков представляет собой остаток по модулю μi(x), где i = 1, 2, 3, то получаем полиномы 
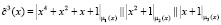. Третий подблок ключевой гаммы имеет вид 
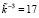. Воспользуемся (8) и расшифруем с помощью МК:
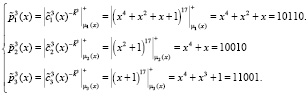
Тогда третий блок расшифрованного текста равен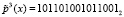 
.
Полученные результаты показали, что, используя разработанный метод нелинейного шифрования данных на основе возведения в степень по модулю с использованием МК, можно сократить временные затраты. В представленном примере показан переход от обработки 15-разрядных данных к параллельным криптографическим преобразованиям трех пятиразрядных операндов, что позволяет повысить скорость нелинейного шифрования в 3 раза.
Выводы
В работе представлен разработанный метод нелинейного шифрования данных на основе возведения в степень по модулю с использованием МК. С целью сокращения временных затрат на зашифрование было предложено использовать независимые параллельные вычисления по модулю неприводимых многочленов. В представленном примере показан переход от обработки 15-разрядных данных к параллельным криптографическим преобразованиям трех пятиразрядных операндов, что позволяет повысить скорость нелинейного шифрования в 3 раза.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.