Интегральные модели достаточно часто используются для описания и моделирования технических систем [1, с. 12–18]. Если система является стационарной (т.е. ее параметры не меняются во времени), то для ее описания применяется интегральное уравнение Вольтера I рода [2, с. 25–29]:
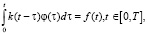(1)
где k(t) – импульсная переходная функция (ИПФ) системы;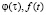 
– ее входной и выходной сигналы. Техническую реализуемость системы определяет условие
k(t) = 0 при t < 0. (2)
Применительно к модели (1), задача непараметрической идентификации [2, 3] системы сводится к вычислению оценки для k(t) по измеренным значениям входного и выходного сигналов идентифицируемой системы.
Сформулированная задача идентификации некорректна, поскольку могут не удовлетворяться одно или несколько условий корректности по Адамару [4, с. 15–18; 5, с. 9]. Наиболее часто нарушается условие устойчивости решения к погрешностям (ошибкам) исходных данных, когда малые погрешности могут вызвать сколь угодно большие ошибки решения. Для построения устойчивых решений некорректных задач используются специальные методы регуляризации, как детерминированные [4, c. 38–56], так и статистические [5, c. 124–129]. В работе авторов [6] был построен эффективный алгоритм, вычисляющий оценку ИПФ из решения интегрального уравнения Вольтера II рода, что является уже корректно поставленной задачей. Однако при этом необходимо было вычислить первые производные от входного и выходного сигналов, что в свою очередь также является неустойчивой задачей. Для устойчивого вычисления этих первых производных использовались сглаживающие кубические сплайны (СКС). Применяемый алгоритм оценивания оптимального параметра сглаживания СКС (из условия минимума среднеквадратической ошибки сглаживания [5, с. 65–67]) позволил вычислять первые производные с приемлемыми ошибками, что обусловило устойчивое решение задачи идентификации даже при больших значениях погрешностей измерения выходного и входного сигналов идентифицируемой системы.
В ряде случаев зарегистрированные значения входного и выходного сигналов могут содержать аномальные измерения, которые значительно (в разы) отличаются от близлежащих измерений, и их появление можно объяснить наличием шумовой составляющей (импульсного шума), дисперсия которой существенно (на два и более порядков) отличается от дисперсии шумов измерений других значений сигналов. Аномальные измерения могут быть обусловлены сбоями в измерительной системе, канале связи, регистрирующей аппаратуре и т.п. К сожалению, СКС очень слабо сглаживает такие импульсные шумы, и это обуславливает большие ошибки в вычислении первых производных, что в свою очередь приводит к существенным ошибкам идентификации ИПФ динамической системы.
В данной работе предлагается новый двухшаговый алгоритм идентификации, на первом шаге которого эффективно фильтруются аномальные измерения (т.е. удаляется импульсный шум) с использованием пространственно-локальных фильтров, а на втором шаге осуществляется построение СКС по фильтрованным значениям входного и выходного сигнала, вычисления первых производных и построение устойчивого решения с использованием алгоритма, изложенного в работе [6]. Особое внимание уделяется оцениванию оптимальных параметров используемых алгоритмов обработки, что позволяет получать решения с наименьшей ошибкой идентификации.
Метод исследования
В работе [6] устойчивый алгоритм идентификации строится переходом от уравнения (1) к уравнению задачи идентификации, которое при выполнении условия (2) имеет вид
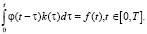(3)
Путем дифференцирования этого уравнения по переменной t и выполнения несложных преобразований, приходим к интегральному уравнению Вольтера II рода вида
,
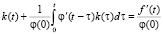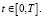(4)
Для устойчивого дифференцирования зашумлённых входного и выходного сигналов идентифицируемой системы в работе [6] использовались сглаживающие кубические сплайны (СКС). Напомним, что функция Sφ(x) называется кубическим сплайном на интервале [0, T] с узлами
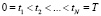, (5)
если: а) на каждом отрезке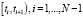 
, функция Sφ(t) представляет собой полином третьей степени вида
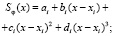(6)
б) функция Sφ(t) является дважды непрерывно дифференцируемой на всем интервале [0, T].
В работе [6] для устойчивого вычисления первых производных входного и выходного сигналов использовался естественный сглаживающий кубический сплайн – функция Sφ,α(t), которая одновременно удовлетворяет естественным краевым условиям относительно второй производной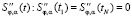 
и доставляет минимальное значение функционалу [5, с. 42–44; 7, с. 124–132]:
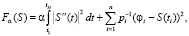(7)
где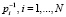 
– весовые множители, 
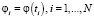– значения функции φ(t) в узлах сетки (5), для которой строится СКС. В рассматриваемой задаче идентификации это зашумленные значения входного и выходного сигналов идентифицируемой системы. Меняя параметр сглаживания α в интервале 
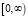, можно менять ошибку сглаживания. Выбор параметра α из условия минимума среднеквадратической ошибки сглаживания рассмотрен в работах [5, 6]. Вычисление коэффициентов 
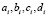при заданном параметре α подробно изложено в [5, с. 45–49].
Рассмотрим поведение сглаживающего сплайна при наличии аномальных измерений (АИ). В качестве иллюстрации на рис. 1 сплошной линией показаны точные значения входного сигнала, точечной кривой – зашумленные значения (относительный уровень шума 10 %), штрих-точечной кривой – измеренные значения, содержащие АИ (вероятность появления АИ равна 0,02).
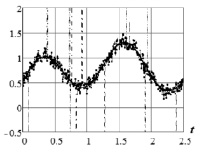
Рис. 1. Измеренные значения входного сигнала
На рис. 2 точечной кривой показаны значения СКС, построенного по измерениям, не содержащим АИ, штрих-точечная кривая – значения СКС, построенного по измерениям, содержащим АИ. Параметр сглаживания для этих двух сплайнов был одинаков и равен α = αW, где αW – оценка оптимального параметра сглаживания (подробнее см. [6]). Видно, что второй СКС содержит осцилляции, вызванные АИ, которые дадут существенные ошибки при вычислении первой производной и, соответственно, большую ошибку в решении уравнения (4). Неудовлетворительное сглаживание АИ обусловлено вторым слагаемым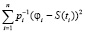 
функционала (7) (слагаемое называется функционалом невязки). Наличие квадрата разности 
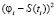«заставляет» сплайн «приближаться» к аномальному измерению и тем самым не удается эффективно сгладить данное АИ.
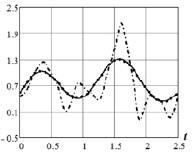
Рис. 2. Значения сглаживающих сплайнов
Для того чтобы сделать алгоритм идентификации нечувствительным (т.е. робастным) к АИ, возможны два подхода:
– заменить квадратичный функционал невязки в (7) на другой, аналогичный функционалу, используемому в методах робастного оценивания коэффициентов уравнения регрессии при наличии АИ (например, на сумму модулей);
– предварительно удалить (отфильтровать) АИ, а затем сгладить оставшийся шум сглаживающим кубическим сплайном.
Первый подход, когда строится робастный сглаживающий сплайн, достаточно сложен и трудоемок [8, 9]. Поэтому в данной работе предлагается робастный алгоритм идентификации, являющийся реализацией второго подхода.
Результат исследования. Робастный двухшаговый алгоритм идентификации
Предположим, что зашумлённые значения входного и выходного сигналов допускают следующие представления:
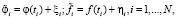(8)
где ξi, ηi – шумы измерения. Для статистического описания АИ введем следующие модели шумов ξi, ηi. Шум измерения входного сигнала ξi с вероятностью 1 – pξ имеет нулевое среднее и дисперсию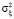 
, а с вероятностью pξ – нулевое среднее и дисперсию 
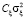, где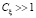 
, т.е. с вероятностью pξ появляется импульсная составляющая шума измерения. Если эта вероятность равна нулю, то такой шум (без импульсной составляющей) будем называть однородным. Шум измерения выходного сигнала ηi с вероятностью 1 – pη имеет нулевое среднее и дисперсию 
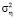, а с вероятностью pη – нулевое среднее и дисперсию 
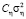, где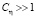 
. На рис. 1 показаны АИ при pξ = 0,02 и Cξ = 400.
На первом шаге предлагаемого алгоритма идентификации осуществляется нелинейная фильтрация с использованием комбинированного фильтра (КФ) [10]. Его выходной сигнал определяется соотношением (при фильтрации входного сигнала):
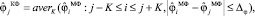(9)
где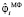 
– результат фильтрации медианным фильтром (МФ), определяемый выражением
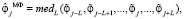(10)
где medL – функция, вычисляющая медиану из 2L + 1 значений, попавших в апертуру фильтра (указаны в скобках). Заметим, что МФ хорошо фильтрует импульсные шумы и сохраняет контрастные составляющие в отфильтрованном сигнале. Усреднение в КФ (сглаживание оставшихся однородных шумов) происходит только для значений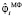 
из интервала 
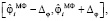что предотвращает сглаживание контрастных составляющих точного сигнала. Таким образом, КФ устраняет импульсные шумы и успешно сглаживает однородные остаточные шумы, при этом размеры апертур удовлетворяют неравенству K ≥ L. Если величина K = 0, то КФ превращается в МФ. Если величина L = 0, то КФ превращается в интервальный фильтр скользящего среднего. Величину Δφ можно определить соотношением: 
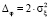. Аналогичный КФ используется для фильтрации выходного сигнала.
На втором этапе по отфильтрованным значениям входного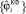 
и выходного 
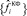сигналов строятся сглаживающие кубические сплайны 
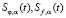с производными 
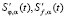соответственно. Параметр сглаживания α выбирался на основе критерия оптимальности, приведенного в работе [6] и подробно рассмотренного в работе [5]. Этот критерий позволяет вычислить оценку αW для оптимального параметра сглаживания αopt, который минимизирует СКО сглаживания. После построения сплайнов и вычисления их первых производных формируется матрица Ф размером (N – 1)×(N – 1), элементы которой определяются как: при i < j, Фi,j = 0; при i ≥ j,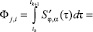 
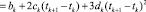, где k = j – i. Сформированная матрица Ф позволяет аппроксимировать уравнение (4) системой линейных алгебраических уравнений (СЛАУ) вида (подробнее в работе [6]):
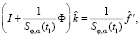(11)
где I – единичная матрица размером (N – 1)×(N – 1), а вектор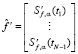 
составлен из значений первой производной выходного сигнала в узлах сетки. Решением этой системы будет вектор 
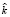, проекции которого являются оценками для значений 
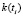ИПФ идентифицируемой системы.
Результаты численных исследований
Приведем некоторые результаты вычислительного эксперимента, выполненного для исследования точности идентификации предложенным алгоритмом. В качестве тестовой ИПФ была взята ИПФ, график которой показан сплошной кривой на рис. 3 (соответствует колебательному звену второго порядка). Значения выходного и входного сигналов искажались погрешностями, подчиняющимися нормальному распределению с относительными уровнями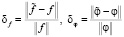 
, где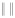 
– евклидова норма вектора, f, φ – векторы, составленные из точных значений выходного и входного сигналов, 
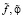– векторы зашумленных значений. В отсутствии АИ δφ = 0,10, δf = 0,10, при наличии аномальных измерений (pξ = 0,02, Cξ = 400, pη = 0,02, Cη = 400) – δφ = 0,358, δf = 0,421. На рис. 3 штрих-точечной кривой показаны значения ИПФ, вычисленные алгоритмом работы [6], когда сглаживающие сплайны строились по АИ и имели из-за этого большие ошибки сглаживания (см. штрих-точечную кривую рис. 2). После сглаживания СКС имеем относительные уровни ошибок сглаживания δφ = 0,311, δf = 0,591. В этом случае относительная ошибка идентификации 
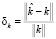была равна 1,258, которая говорит об очень плохой точности идентификации.
Приведем некоторые количественные характеристики предлагаемого двухступенчатого алгоритма идентификации. После выполнения на первом шаге фильтрации с использованием КФ относительные уровни остаточных шумов были равны: δφ = 0,052, δf = 0,061. Сравнивая с уровнями шумов исходных сигналов (δφ = 0,358, δf = 0,421), видим существенное уменьшение уровней шума и удаление импульсных составляющих. После сглаживания СКС остаточного шума имеем: δφ = 0,038, δf = 0,049. На рис. 3 точечной кривой показаны значения ИПФ, вычисленные двухшаговым алгоритмом идентификации, при этом относительная ошибка идентификации составила δk = 0,138. Заметим, что относительная ошибка идентификации алгоритмом работы [6] при отсутствии аномальных измерений была равна 0,131.
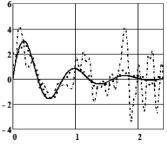
Рис. 3. Импульсная переходная функция и ее оценки
Заключение
Предложенный двухшаговый алгоритм идентификации позволяет решать задачу идентификации с приемлемой точностью даже при наличии в измеряемых сигналах идентифицируемой системы импульсного шума. Отчасти это обусловлено тем, что матрица СЛАУ хорошо обусловлена (число обусловленности зависит от полосы спектра мощности входного сигнала и чаще всего не превышает 1000), и поэтому ошибки, возникающие при дифференцировании выходного сигнала, оказывают существенно меньшее влияние на точность построенного решения по сравнению с ошибками правой части уравнения (3), решаемого с использованием регуляризирующего алгоритма на основе дискретного преобразования Фурье [5]. Следует отметить, что общие затраты машинного времени на построение решения предложенным алгоритмом возрастают (из-за пространственно-локальной фильтрации) незначительно и это увеличение составляет примерно 25–30 %.