С учетом климатических условий северной строительно-климатической зоны Российской Федерации, монолитное бетонирование в большинстве случаев проводится при отрицательных температурах [1]. Например, в районах Арктической зоны Российской Федерации в зимнее время производится порядка 50–75 % бетонных работ [2].
Как известно, при бетонировании любых строительных конструкций, независимо от принятого способа производства работ, в бетоне возникает напряженное состояние, связанное с неравномерностью температурного поля по всему телу конструкции [3]. Поэтому особым условием является обеспечение такого термонапряженного состояния конструкции, при котором в бетоне не возникают деструктивные процессы [4].
Одним из наиболее технологичных и эффективных методов зимнего бетонирования является способ контактного обогрева забетонированных конструкций [5]. Реализация данного метода достигается обогревом бетона и железобетона в термоактивной опалубке с принципиально новой системой распределения тепла на основе тепловых труб, работающих от любого источника тепловой энергии.
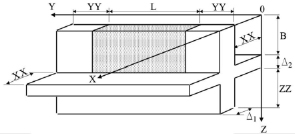
Рис. 1. Идеализированная конструктивная схема участка стены с учетом ранее построенных фрагментов конструкций здания
Анализ существующих методов зимнего бетонирования выявил эффективность метода электрообогрева монолитных конструкций с использованием различных вариантов термоактивных опалубочных форм [4–6]. В качестве греющего элемента предлагается использовать разновидность тепловой трубы – двухфазный термосифон. Двухфазный термосифон представляет собой оборудование для транспортировки теплоносителя, в котором теплота постепенно передается посредством суммарного эффекта скрытого образования пара по всему объему стенок труб. Это объясняется испарением жидкости теплоносителя в зоне подключения тепла и конденсации ее паров в зоне отвода. При этом полностью замкнутую циркуляцию теплоносителя приводит в действие сила тяжести.
До настоящего времени разновидности двухфазных термосифонов в строительной индустрии не нашли должного использования. Наиболее перспективное практическое применение двухфазных термосифонов открывается при бетонировании сборных и монолитных железобетонных (бетонных) строительных конструкций при отрицательной температуре наружного воздуха. С учетом рассмотренных выше положений следует отметить о необходимости дополнительного всестороннего исследования двухфазных термосифонов с использованием методологии строительной теплофизики и теплотехники.
Цель исследования: разработка метода расчетного обоснования параметров энергосберегающего и щадящего режима тепловой обработки бетона с помощью двухфазного термосифона.
Материалы и методы исследования
В математическом моделировании использованы классические уравнения теплофизики, не требующие доказательства достоверности [7, 8]: дифференциальное уравнение теплопроводности; условие Стефана; классические граничные условия I (задана температура бетона на границе), II (задана интенсивность теплового потока на границе), III (теплообмен на границе по закону Ньютона), IV (условие теплового примыкания двух твердых тел) рода. Обработка расчетных и экспериментальных данных выполнена на программах MathCAD 2001i и Microsoft Office EXCEL.
Результаты исследования и их обсуждение
Дифференциальные уравнения теплопроводности (1) и (2) аппроксимированы по методу неявной разностной схемы дробных шагов, разработанной профессором Н.Н. Яненко [8]. По качественным и количественным параметрам глубины проникновения теплового потока на плиту перекрытия, в уравнении (2) следует учесть граничные условия III рода. Такой подход не приводит к значительному усложнению дифференциальных уравнений, а также математической модели в целом.
Идеализированная конструктивная схема участка стены с учетом ранее построенных фрагментов конструкций здания показана на рис. 1.
Сегменты конструкции стен (рис. 1) являются пространственным сооружением (бетонируемая стена, ранее возведенные участки стены и плит перекрытий), что приводит к решению так называемой трехмерной задачи. Конструктивная схема участка стены имеет толщину Δ1, а плита перекрытия – Δ2. Область теплового влияния на ранее возведенные фрагменты стен по осям Y и Z – YY и ZZ. XX – это тепловые потоки, заданные молекулярной теплопроводностью бетона в ранее уложенной плите перекрытия.
В работе [9] автором ранее был рассмотрен фрагмент другой конструкции здания. По аналогии с которым в разрабатываемой модели следует также учесть потоки тепла, исходящие от ранее возведенных участков конструкции стены, так и от плиты перекрытия. Вышерассмотренные условия предопределяют возможность построения трехмерной математической модели:
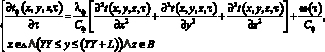 (1)
(1)
где tф, λф, Cф – температура, коэффициент теплопроводности и удельная теплоемкость опалубки с двухфазными термосифонами.
(1) – дифференциальное уравнение теплопроводности с объемно распределенным источником тепла для бетонируемого фрагмента конструкции.
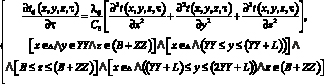 (2)
(2)
где tб, λб, Cб – температура, коэффициент теплопроводности и удельная теплоемкость тяжелого бетона.
(2) – дифференциальное уравнение теплопроводности для ранее возведенных участков конструкции.
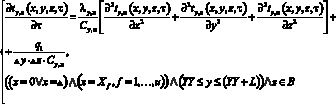 (3)
(3)
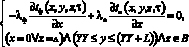 (4)
(4)
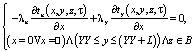 (5)
(5)
(3), (4), (5) – уравнения теплового примыкания опалубки к телу бетонируемого фрагмента в случае, когда линейный источник тепла q1 нельзя приводить к условно плоскому источнику тепла qon(τ).
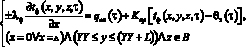 (6)
(6)
(6) – то же в случае, когда можно линейный источник тепла привести к условно плоскому, является комбинацией граничных условий IIи III родов.
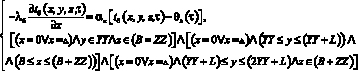 (7)
(7)
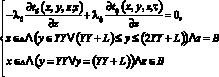 (8)
(8)
(7), (8) – граничные условия IV рода на границах теплового контакта возводимого фрагмента и ранее возведенных участков конструкции.
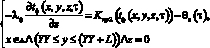 (9)
(9)
(9) – граничные условия III рода на боковых поверхностях бетонируемого фрагмента.
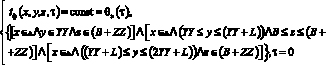 (10)
(10)
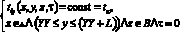 (11)
(11)
(10), (11) – начальные условия.
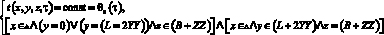 (12)
(12)
(12) – граничные условия I рода в конце зон теплового влияния бетонируемого фрагмента.
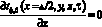 (13)
(13)
(13) – условие тепловой симметрии при x = Δ/2.
Численное решение дифференциальных уравнений (1–13) выполнено с помощью специального алгоритма на сертифицированном программном обеспечении. Следующим этапом расчета является, аппроксимация уравнения (1) по неявной разностной схеме дробных шагов Н.Н. Яненко [8]:
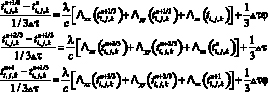 (14)
(14)
Решение уравнений (14) имеет вид
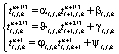 (15)
(15)
По аналогии с (15) запишем
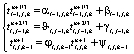 (16)
(16)
Решая совместно уравнения (15) и (16), находим
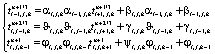 (17)
(17)
После подстановки соответствующих выражений (15–17) имеем
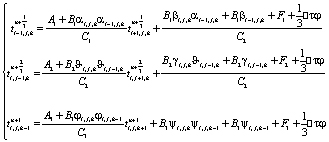 (18)
(18)
Сравнивая соответствующие уравнения (15) и (18), находим прогоночные коэффициенты:
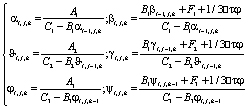 (19)
(19)
Проверка теоретических данных осуществлялась экспериментально на фрагментах бетонной стены размерами 1,2×1,2×0,2 м с толщиной стальной формы 3 и 6 мм при шагах нагревателей от 100 до 300 мм (удельной мощности 200–1200 Вт/м2) и температуре наружного воздуха от –10 до –30 °С.
Полученные экспериментальные данные обработаны с использованием стандартных методов математической статистики и показаны в виде номограммы для определения оптимального шага расположенных вплотную линейных нагревателей и на расстоянии 30 мм к форме толщиной от 1 до 6 мм, обеспечивающего температурные градиенты на поверхности формы в пределах 0,8–5 °С (рис. 2).
По результатам измерений были построены графики изменения температурных полей на форме при различном шаге нагревателей и расстоянии между формой и нагревателем (рис. 3).
Рис. 2. Номограмма для определения основных характеристик линейных нагревателей
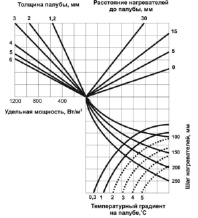
Рис. 3. Графики изменения температурных перепадов на форме при различном шаге линейных нагревателей: 1 – вплотную к форме; 2, 3 и 4 – на расстоянии 5, 14 и 30 мм от формы
Данные графиков и номограммы показывают причинно-следственную взаимосвязь между изменениями удельной мощности, толщиной формы, расстоянием нагревателей до стенки формы, шагом нагревателей, а также температурным градиентом. На основании вышерассмотренных положений и расчетов оптимальная скорость подъема температуры для среднемассивных монолитных конструкций составляет не более 10 град/час. Приведенными расчетами выявлено, что возможность энергосбережения разработанным методом составляет 20 % при гарантированном отсутствии деструктивных процессов в бетоне, ранее установленные С.Н. Шпанко [10].
Выводы
1. Предложен способ термообработки монолитных бетонных конструкций при бетонировании стены с нагревателями из двухфазных сифонов (разновидность тепловых труб), работающих от любых видов тепловой энергии.
2. Теоретически обоснована и экспериментально подтверждена математическая модель температурных полей, исходящих от конструкции стены, примыкающей к ранее уложенным участкам стены и плит перекрытий.
3. Разработанная математическая модель дает возможность заменить линейный источник тепла на условно цилиндрический, что, в свою очередь, заметно упрощает процесс написания программного кода на языке программирования.
4. Разработана методика графического расчета для определения оптимального шага линейных нагревателей при различном расположении их на форме.
5. При внедрении данного способа подтверждена возможность энергосбережения до 20 % с гарантированным качеством выполнения бетонных работ при отрицательных температурах, ранее установленных С.Н. Шпанко.



