В последнее десятилетие наиболее развитые индустриальные страны активно занимаются производством и внедрением транспортных средств на электрическом приводе, поскольку автомобили с карбюраторными и дизельными двигателями наносят существенный ущерб окружающей среде, стремительно дорожают бензин и солярка, а также повышается стоимость обслуживания автомобилей [1, 2]. На сегодняшний день для производства электромобильных средств используются двигатели переменного и постоянного тока [3, 4]. Причём эффективность последних во многом обуславливается эффективностью цифровых регуляторов положения, скорости и тока [5]. Разработка цифрового регулятора, исходя из континуальной модели регулятора [6, 7]
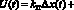
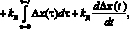 (1)
(1)
традиционно сводится к обсчету формулы пропорционально-интегрально-дифференциального (ПИД) регулятора [7, 8], на основе которой формируется сигнал широтно-импульсной модуляции:
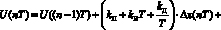
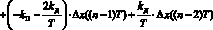 , (2)
, (2)
где t = nT (n – момент времени (n = 0, 1, 2,...), T – период опроса датчиков); U(nT) и 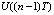 – управляющие воздействия в соответствующий момент времени; Δx(nT) – рассогласование (отклонение, ошибка, невязка) в текущий (Δx(t) пропорционален
– управляющие воздействия в соответствующий момент времени; Δx(nT) – рассогласование (отклонение, ошибка, невязка) в текущий (Δx(t) пропорционален 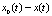 , где x0(t) – задающее воздействие, x(t) – регулируемая величина);
, где x0(t) – задающее воздействие, x(t) – регулируемая величина); 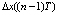 и
и 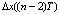 – ошибки в соответствующий момент времени; kП, kИ, kД – настроечные параметры регулятора. Сравнительное исследование традиционной формулы цифрового регулирования (2) [9, 10] показало, что различные диапазоны значений настроечных параметров (kП, kИ, kД) делают эффективными как формулы вычисления управляющего воздействия (2), так и формулы с раскрытием интеграла в (1) по методу трапеций:
– ошибки в соответствующий момент времени; kП, kИ, kД – настроечные параметры регулятора. Сравнительное исследование традиционной формулы цифрового регулирования (2) [9, 10] показало, что различные диапазоны значений настроечных параметров (kП, kИ, kД) делают эффективными как формулы вычисления управляющего воздействия (2), так и формулы с раскрытием интеграла в (1) по методу трапеций:
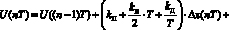
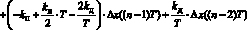 ; (3)
; (3)
и по методу Симпсона:
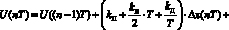
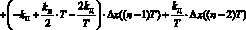 для
для 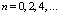 ,
,
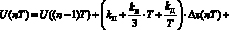
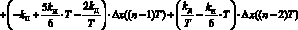 для
для 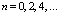 . (4)
. (4)
Однако различные формулы обуславливают различную форму переходного процесса и установившегося режима. Не всегда удается удовлетворить требования регулирования по запасу устойчивости при использовании одной из формул. Возникает потребность в методе, который совмещал бы в себе основные позитивные свойства формул (2)–(4).
В работе сделана попытка формулирования подхода к построению основ методологии корректирования процессов цифрового ПИД регулирования на примере оценки наиболее быстродействующего токового контура двигателя постоянного тока.
Научная проблема как индикатор цели исследования
Поскольку в теории тяговых электрических машин и в теории автоматического управления отсутствуют методики смешанного типа, разработка методов автоматического перехода на различные формулы или в целом на корректировку процесса цифрового регулирования является актуальной.
Основная идея корректирования
Идея корректировки цифрового регулирования в текущий момент времени t = nT заключается:
1) в формировании управляющих воздействий 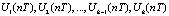 по дискретным математическим моделям регулятора
по дискретным математическим моделям регулятора 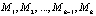 ;
;
2) в моделировании для следующего момента времени t = (n + 1)T реакций объекта управления 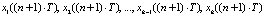 и соответствующих рассогласований
и соответствующих рассогласований 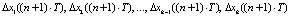 ;
;
3) в выполнении предиката, т.е. поиск минимального рассогласования:
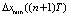
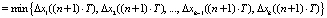 ,
,
и выборе наилучшего управляющего воздействия из 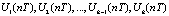 , соответствующего минимальному отклонению
, соответствующего минимальному отклонению 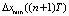 .
.
Тогда метод корректировки цифрового регулирования можно описать следующей последовательностью действий:
1) выбираются дискретные математические модели регулятора 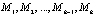 с соответствующими значениями настроечных параметров;
с соответствующими значениями настроечных параметров;
2) задаются критерии выбора управляющего воздействия, используемые при совпадении значений невязок, смоделированных для момента времени t = (n + 1)T. Например:
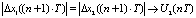 , …,
, …,
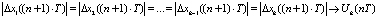 ;
;
3) задаётся уставка x0(t) (задающее воздействие);
4) формируются управляющие воздействия в текущий момент времени:
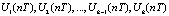 ;
;
5) моделируются для следующего момента времени t = (n + 1)T реакции объекта управления, рассчитанные на основе сформированных на предыдущем шаге управляющих воздействий и текущего значения реакции объекта управления x(nT):
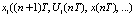 ,
, 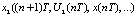 , …,
, …,
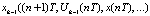 ,
, 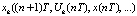 ;
;
6) моделируются рассогласования, рассчитанные на основе полученных на предыдущем шаге реакций объекта управления:
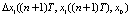 ,
, 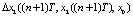 , …,
, …,
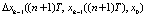 ,
, 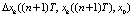 ;
;
7) выбирается абсолютное минимальное значение рассогласования из рассчитанных на предыдущем шаге рассогласований:
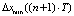
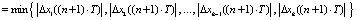 ;
;
8) выбирается управляющее воздействие U(nT), соответствующее Δxmin((n + 1)T) с учетом критериев выбора, сформулированных на втором шаге:
если 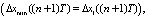 то
то 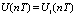 ; …;
; …;
если 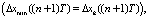 то
то 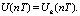
Очевидно, что сформулированные идея и метод корректировки будут эффективны в реализации при наличии следующих инструментальных средств корректировки:
а) по оперативному изменению набора математических моделей регулятора;
б) по вариации критериев выбора управляющего воздействия;
в) по выбору языка представления уставки;
г) по выбору языка представления невязки и его формальным аналогам.
В качестве примера моделирования для корректирования процессов цифрового регулирования использовалась упрощённая модель токового контура двигателя постоянного тока электромобильного агрегата BMW 325iX [11]:
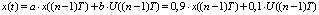 ,
,
которая показала продуктивность предложенного метода корректирования [12].
Проблематика корректирования
Следуя традиционным представлениям [13], принято считать, что устойчивость – свойство системы возвращаться в исходный или близкий к нему установившийся режим из различных начальных состояний. Если t – время, yi – переменные, описывающие состояние непрерывной системы (НС) со сосредоточенными параметрами (замкнутый контур ПИД регулирования), то она описывается в виде системы обыкновенных дифференциальных уравнений или в векторно-матричной форме:
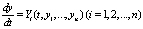 , (5)
, (5)
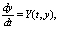 (6)
(6)
где 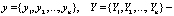 n – мерные векторы-столбцы. Если η = η(t) –некоторое частное решение уравнения (6) (невозмущенное движение), устойчивость которого требуется исследовать, а разность x = y – η(t) – это отклонение решения y(t) от η(t), то переменные xi = yi – ηi удовлетворят уравнениям возмущенного движения:
n – мерные векторы-столбцы. Если η = η(t) –некоторое частное решение уравнения (6) (невозмущенное движение), устойчивость которого требуется исследовать, а разность x = y – η(t) – это отклонение решения y(t) от η(t), то переменные xi = yi – ηi удовлетворят уравнениям возмущенного движения:
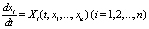 , (7)
, (7)
где 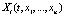 =
= 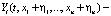
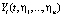 или в векторно-матричной форме:
или в векторно-матричной форме:
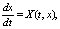 (8)
(8)
где 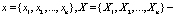 n – мерные векторы-столбцы, причём
n – мерные векторы-столбцы, причём 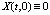 .
.
Несмотря на многообразие определений устойчивости (устойчивость по Лагранжу для равновесия консервативных механических систем, орбитальная устойчивость, структурная устойчивость, L2-устойчивость, устойчивость инвариантного множества и др.), её основная идея выражена в представлениях об устойчивости по академику А.М. Ляпунову. Исходя из предположения о том, что функции Xi удовлетворяют условиям существования и единственности решения системы (7), невозмущенное движение системы 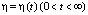 называется устойчивым при
называется устойчивым при 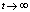 , если для любых ε > 0 и
, если для любых ε > 0 и 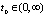 существует
существует 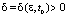 такое, что для всех возмущённых движений, удовлетворяющих условию
такое, что для всех возмущённых движений, удовлетворяющих условию 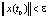 , следует
, следует 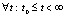 справедливость неравенства
справедливость неравенства 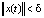 , где норма вектора x представляется евклидовой нормой
, где норма вектора x представляется евклидовой нормой 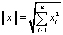 или нормой Манхеттена
или нормой Манхеттена 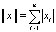 . Для линейных непрерывных систем (ЛНС) уравнение (8) сводится к виду
. Для линейных непрерывных систем (ЛНС) уравнение (8) сводится к виду
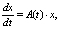 (9)
(9)
где 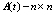 -матрица, элементы которой в общем случае являются функциями времени, а когда
-матрица, элементы которой в общем случае являются функциями времени, а когда 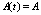 – постоянная матрица, справедливо суждение: ЛНС (9) с постоянной матрицей A устойчива тогда и только тогда, когда все характеристические числа (собственные значения)
– постоянная матрица, справедливо суждение: ЛНС (9) с постоянной матрицей A устойчива тогда и только тогда, когда все характеристические числа (собственные значения) 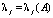 матрицы A обладают неположительными вещественными (действительными) частями:
матрицы A обладают неположительными вещественными (действительными) частями:
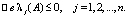 (10)
(10)
При этом характеристические числа с нулевой вещественной частью допускают лишь простые элементарные делители. Характеристические числа матрицы A являются корнями её характеристического уравнения:
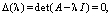 (11)
(11)
где I – единичная матрица. Оценивать знаки действительных частей корней уравнения (11) – непростая задача, но это можно сделать, не решая его, посредством критериев устойчивости Рауса, Гурвица, Михайлова или Найквиста для систем (9) с постоянной матрицей.
Такое представление устойчивости в практическом аспекте естественно интерпретируется как свойство затухания переходного процесса с течением времени, а областью устойчивости системы обусловливается множеством сочетаний ее параметров, при которых выполняется общее условие устойчивости ЛНС, в том числе для линейных систем автоматического управления и регулирования. Граничными (критическими) называют такие сочетания параметров, при которых система находится на границе устойчивости. При этом нередко требуется оценить влияние одного параметра системы на ее устойчивость при постоянных (номинальных) значениях остальных параметров. В этом случае определяется запас устойчивости – диапазон значений параметра от номинального до граничного, как правило, посредством [14]: а) критерия устойчивости Гурвица, который задаёт запас устойчивости системы тем, что алгебраические неравенства соответствующих детерминантов были больше заданной положительной величины, определяющей запас устойчивости; б) критерия устойчивости Михайлова, который обеспечивает исследуемую систему заданным запасом устойчивости a, если кривая Михайлова, удовлетворяя критерию устойчивости, не заходит в круг радиуса a с центром в начале координат. Это требование определяет удаление кривой Михайлова от начала координат во всех точках не менее чем на заданную величину a; в) критерия устойчивости Найквиста как амплитудно-фазового критерия, например, в двух вариантах. В первом случае считают, что система обладает заданным запасом устойчивости a, если амплитудно-фазовая характеристика разомкнутой системы, удовлетворяя критериям устойчивости, не заходит в круг радиуса a с центром в точке с координатами (–1; j0). Во втором – оценивают запас устойчивости по фазе и запас устойчивости по амплитуде. Запас устойчивости по фазе определяется величиной, на которую должно возрасти запаздывание по фазе в системе на частоте среза, чтобы система оказалась на границе устойчивости. Запас устойчивости по амплитуде определяется величиной допустимого подъема логарифмической амплитудной характеристики, при котором система окажется на границе устойчивости, то есть запас по амплитуде представляет собой запас по коэффициенту передачи разомкнутой системы по отношению к его критическому по устойчивости значению.
Значительная смысловая нагрузка понятия устойчивости и запаса устойчивости делает методики их определения структурообразующими финальными мероприятиями процессов синтеза цепей регулирования и поэтому функционал установления и оценки запаса устойчивости для соотношений (5)–(11) должен быть включён в инструментарий корректировки и должен отрабатываться системами моделирования уже на первых этапах сформулированного метода корректировки цифрового регулирования.
Однако здесь не исключена возможность, во-первых, нарушения устойчивости самого метода корректировки при добавлении алгоритмов определения запаса устойчивости и, во-вторых, результативности достижения такого процесса корректирования, при котором совмещались бы высокая точность регулирования с наибольшими показателями запаса устойчивости на множестве моделей регулирования 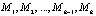 .
.
Заключение
Очевидно, что эффективность предложенной идеи корректирования определяется инструментарием корректировки для: задания математических моделей регулирования, в том числе настроечных параметров; задания предиката и критериев выполнения предиката; задания параметров цифрового регулятора; задания математической модели объекта управления; проведения моделирования.
Не игнорируя отмеченную проблемность по обеспечению как устойчивости метода корректировки, так и оптимального соотношения прецизионного регулирования с наилучшими показателями запаса устойчивости на заданном множестве моделей регулирования, можно наметить следующую научную новизну работы:
1) предложен новый метод корректировки процессов цифрового регулирования на основе известных математических моделей цифрового ПИД регулирования, отличающийся формированием наилучшего управляющего воздействия в такте превентивной оценки реакции объекта регулирования;
2) предложены инструментальные средства корректировки цифрового регулирования на основе предложенного метода корректировки, обеспечивающие гибкое оперативное изменение процесса регулирования для достижения требуемого запаса устойчивости.
В целом предложенный инструментарий порождает совокупность методов регулирования, и поэтому предложенные разработки можно считать начальным вкладом в построение методологии корректирования цифрового ПИД регулирования электромобильных средств.



