Задача составления оптимального расписания регулирования мощности, коммутируемой группе потребителей электроэнергии при использовании широтно-импульсного метода (ШИМ) является актуальной [1, 2]. В математической модели такого регулирования и математической модели некоторых других задач [3] численное значение результата оптимизации выражается коэффициентом мощности по формуле [1]:
, (*)
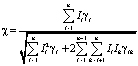где γik – относительная длительность интервала совместного действия импульсов i-го и k-го регуляторов, γi – относительная длительность импульса i-го регулятора в пределах от 0 до 1, n – число регуляторов (также называемых объектами) в группе, Ii – ток нагрузки i-го регулятора, Ik – ток нагрузки k-го регулятора.
В идеальном случае χ = 1, но, как правило, χ < 1. Существуют наборы входных данных этой задачи, для которых невозможно составить расписание, при котором χ = 1. Например, если n = 2, I1 = I2 = 1, γ1 = 0,5, γ2 = 0,6. Требуется максимизировать χ, либо минимизировать целевую функцию C – правую часть суммы под знаком корня в выражении (*), которая при целочисленных токах нагрузки представляет собой целочисленное значение, если вместо относительных длительностей используются абсолютные целочисленные значения. С данной целью ранее разработан ряд алгоритмов с номерами от 1 до 34 [3]. Для решения этой и других задач существует также алгоритм оптимизации последовательности отбора (АОПО), показывающий наивысшие результаты, что касается скорости и качества оптимизации [4]. АОПО минимизирует C, оптимизируя последовательность регуляторов, по которой для них выбираются моменты включения, с помощью метода имитации отжига (ИО) [5]. В данной работе вводятся модификации АОПО, при некоторых параметрах показывающие результаты, превосходящие результаты исходного АОПО.
Цель исследования: определение оптимальных параметров модификаций АОПО для нахождения близких к оптимальным расписаний для ШИМ мощности за ограниченное время.
Материалы и методы исследования
Задачи, решаемые для достижения цели: определить, какие параметры будут исследованы, в каких диапазонах, а также время, требуемое для проведения одного эксперимента; провести серии вычислительных экспериментов при различных наборах обрабатываемых данных; оценить полученные результаты.
Для исследования используются файлы данных f1, f5, содержащие целочисленные Ii и абсолютные γi в диапазоне от 1 до 100, где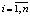 
, n = 40 [3]. С той же целью создан файл данных для n = 28 с целочисленными абсолютными значениями. Численные значения данных файла f1 приводятся в [4], где они интерпретированы как долготы и широты.
Для уменьшения случайных погрешностей исследование проводится при помощи серий вычислительных экспериментов с одинаковыми параметрами. Производится оптимизация набора значений параметров и для этого используется такой метод оптимизации, как метод однокоординатного спуска, что означает следующее. В пространстве дискретных значений параметров выполняется поиск оптимальной точки. Некоторая точка принимается за исходную. Затем анализируются точки, получаемые изменением с переменным шагом значений одной из координат при неизменных прочих координатах. Из результатов анализа выбирается оптимальная точка в качестве текущей. То же самое производится с другими координатами. Критерием останова служит отсутствие более оптимальных точек при последовательном изменении каждой координаты.
Организация вычислительных экспериментов
Определены три группы параметров АОПО: специфические параметры АОПО, параметры применяемого алгоритма ИО и параметр выбора исходной (отправной) точки. К специфическим параметрам относятся:
– R – расстояние в последовательности отбора (ПО), в пределах которого два объекта могут взаимно переставляться. Единица измерения – объект;
– X – число объектов, обменивающихся положениями, т.е. номерами, перед однократным построением расписания согласно полученной ПО с подсчетом C. Это число означает, что X раз производится обмен положениями двух случайно выбираемых объектов.
Параметры метода ИО, используемые в исходном варианте АОПО, следующие: «Заданная температура», «Начальное число итераций» и «Увеличение числа итераций» [3]. От изменения перечисленных параметров можно в данном случае отказаться для сокращения числа параметров, так как они в совокупности однозначно определяют общее число итераций NI, которое в дальнейшем исследовании неизменно. Таким образом, исследуемой величиной в алгоритме ИО является вероятность перехода к худшему решению P.
Исследуются три модификации АОПО. В первой модификации всегда Р ≡ 0.
Во второй модификации применяется схема Больцмана, суть которой следующая [6]. Приближенное значение P можно определить по формуле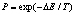 
, где ΔE – разность между значениями C в текущей и исследуемой точках, T – текущая температура. Возможны различные схемы определения T. Одна из схем называется схемой Больцмана: 
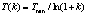, где k – номер шага, Tmin – начальная температура, которую можно задать как константу. В последующих экспериментах Tmin = 5. Для определения общего числа шагов предлагается разделить NI на параметр DS – целое число.
Третья модификация АОПО применяет другую схему определения T, называемую схемой Коши, при которой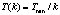 
[7].
При проведении серий экспериментов с целью сравнения результатов требуется, чтобы процессорное время, выделяемое на каждый эксперимент, было постоянным. Это время напрямую зависит от NI. Поэтому NI = const, и единственным исследуемым параметром алгоритма ИО остаётся DS.
Параметром выбора исходной точки является A – номер алгоритма [3], по которому она генерируется.
Для определения времени, выделяемого для каждого эксперимента, вначале исследуется первая модификация алгоритма при A = 2 с файлом f1. При следующей совокупности параметров время единичного эксперимента составляет 20–20,5 мин на ноутбуке с тактовой частотой процессора 1500 МГц: X = 3, R = 8, NI = 588000. Число NI неизменно, поэтому представим совокупность параметров в виде вектора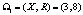 
.
Указанная в минутах длительность выбрана в связи с формой графика зависимости C от времени, приближающейся к затухающей экспоненте. В первую секунду нахождение лучших решений происходит в среднем 4,3 раза. Затем они находятся все более редко, и по истечении нескольких минут для этого могут потребоваться уже минуты.
Через 30 с после запуска алгоритма разность между достигнутым значением и минимальным из когда-либо найденных значением, которое обозначим Cmin, в среднем составляет 30 % от разности между значением C в отправной точке и Cmin. Через 20 мин эта разность все еще находится в пределах 10–14 %. Следовательно, время эксперимента должно составлять не менее 20 мин. Еще более длительное время затрачивать не следует, так как практическая ценность алгоритма связана с разумным временем его применения. Так, в плавильном цехе перерасчет расписания включения электропечей может занимать до 30 мин, но могут применяться микроконтроллеры с тактовой частотой ниже, чем у ноутбука.
Как показывают вычисления, X влияет на время работы алгоритма незначительно, до 3 %, а R совершенно не влияет. Однако на это время влияют исходные данные в файле. Например, при использовании вместо f1 файла f5 время увеличивается в среднем на 13 %. Поэтому, для постоянства времени, серии экспериментов следует проводить с одним и тем же файлом, а разные файлы применять для обобщения результатов разных серий.
Из алгоритма АОПО можно заключить, что 1 ≤ R ≤ n/2, и что X – целое положительное число. Следовательно, для файла f1, 1 ≤ R ≤ 20. Если X = 0, алгоритм не выполняет специфику своей работы, так как ничто в ПО не изменяется. Экспериментально установлено, что X не должно быть более 5 при n = 40. Иначе изменяется одновременно много координат и эффективность алгоритма теряется. Таким образом, 1 ≤ X≤ 5.
Проведение серий вычислительных экспериментов в областях исследования
Серии экспериментов состояли из 10 экспериментов каждая. Вначале проведено исследование для Р ≡ 0.
В качестве начального набора значений параметров использован следующий: X = 1, R = 8 при NI = 588000, A = 2 для файла f1. Проведены серии экспериментов при изменении X от 1 до 5. Минимальное среднее значение C по 10 экспериментам, обозначаемое C10, составило 2877289,9 при X = 2. Среднеквадратическое отклонение Ω при этом также было минимальным и составило 26,9. Крайние точки, в которых X = 1 или X = 5, приводили к максимальным значениям, поэтому выход за их пределы неперспективен для дальнейшего исследования. Таким образом, за дальнейшую основу взят набор параметров Ω2 = (2, 8).
Проведены серии экспериментов для X = 2 и варьировании R от 4 до 20. Крайние значения снова привели к худшим относительно прочих результатам, т.е. не следует выходить за крайние значения. Ни один из результатов не был лучше достигнутого для Ω2.
В связи с перспективностью Ω2, в нем проведена еще одна серия экспериментов для уменьшения случайной ошибки. Получено C10 = 2877309,3, а среднее по 20 экспериментам составило 2877299,6. Это больше, чем для некоторых ранее исследованных наборов параметров. Поэтому для одного из таких наборов, Ω1, повторно проведена серия экспериментов. Полученное среднее по 20 экспериментам составило 2877302,6, что превышает на 3 среднее по Ω2. Таким образом, Ω2 можно считать все еще перспективным.
Для Ω2 всего проведено 140 однократных экспериментов. Получено среднее 2877310,8 с σ = 31,7. При варьировании параметров X от 1 до 5 и R от 4 до 20, включая Ω2, проведено всего 27 серий экспериментов. Получено среднее 2877314,7 с σ = 35,2. Следовательно, среднее для Ω2 ненамного отличается от среднего при других параметрах.
Затем проведено исследование при использовании схемы Больцмана: при DS = 25, X = 2 и X = 3 и при DS = 100, X = 3. C10 различались всего на 0,4, поэтому сделан вывод, что в данной схеме значение DS важной роли не играет.
Среднее значение по двум сериям составило 2877315,5 при σ = 32,6. Это практически не отличается от значений для схемы при Р ≡ 0, поэтому дальнейшее исследование для схемы Больцмана признано нецелесообразным.
Дальнейшее исследование проводилось с использованием схемы Коши. Проведены серии экспериментов при изменении DS со значениями 10, 25, 60, 100, 200 для Ω1. Наихудшие результаты, C10 = 2877316,2 и C10 = 2877312,5, получены при DS = 10 и DS = 200 соответственно; это крайние значения из исследуемого диапазона. Поэтому значения DS < 10 и DS > 200 не рассматривались, исходя из тенденции, что результаты склонны к ухудшению при изменении DS в сторону крайних значений.
Относительно минимальное значение C10 = 2877301,8 с σ = 22,6 получено при DS = 100. Поэтому исследование для X = 2 также проведено для DS = 100. При этом C10 = 2877304,4, что незначительно хуже, чем для Ω1. Таким образом, результаты использования схемы Коши незначительно выше, чем для двух других схем.
Аналогичным образом исследование проводилось с файлом f5. Полученными оптимальными значениями являются X = 2, R = 6. Аналогично проведено исследование для файла, описывающего 28 объектов. Полученными оптимальными значениями параметров являются X = 3, R = 13. Таким образом, для разных файлов к относительным минимумам приводят значения X = 3 при разных R: R = 13 для n = 28, R = 6 и R = 8 для n = 40.
В каждой проведенной серии экспериментов присутствовал относительно близкий к оптимуму результат. Это послужило причиной разработки и исследования четвертой модификации алгоритма, а именно использования метода множественного старта (мультистарта) [8] для АОПО по схеме Коши.
Для файла с данными о 28 объектах при X = 2 варьировалось R, наилучший результат найден при R = 11. При R = 11 варьировалось X, улучшения это не принесло. При X = 2, R = 11 варьировалось число стартовых точек метода мультистарта, обозначаемое MC, от 5 до 160, наилучшее значение C10 найдено при MC = 25.
Собственно алгоритм 3 приводит к худшему результату, чем собственно алгоритм 2, как следует из таблицы [3, с. 53]. Учитывая этот факт, при X = 2, R = 11, MC = 25 проведены эксперименты при A = 3, в итоге C10 найдено худшим. Тот же набор параметров использован по отношению к A = 6, так как алгоритм 6 приводит к наилучшему из результатов работы собственно алгоритмов от 1 до 34 для файла с n = 28, и получено наилучшее значение C10. Далее при варьировании R минимальное значение найдено при R = 4.
Снова исследование проводилось для файла f1. При A = 2, R = 8, X = 2, DS = 100 варьировалось MC, наилучший результат C10 = 2877281,9 выявлен при MC = 50. При этих значениях варьировалось R, лучшего результата не получено. При варьировании X наилучший результат C10 = 2877280,9 получен при X = 1.
Наилучшая стартовая точка C = 2877487 достигается при использовании для f1 алгоритма 34. Соответственно, при A = 34 и варьировании параметров X, R, MC минимальный результат (C10 = 2877242,8 при σ = 6,64) достигнут при R = 4, X = 2, MC = 50. Таким образом, значения X и R для наилучших результатов файлов с n = 28 и n = 40 совпали, а значения MC и A разные.
Результаты исследования и их обсуждение
В исследовании для файла f1 найден новый Cmin = 2877230 при χ = 0,9999968062. Для этого в соответствии с номерами объектов в [4] получено следующее расписание, указывающее моменты включения регуляторов: 1, 61, 86, 18, 54, 28, 50, 77, 77, 6, 88, 12, 6, 87, 92, 12, 93, 65, 33, 36, 54, 53, 45, 76, 20, 87, 28, 84, 93, 82, 1, 8, 13, 91, 67, 87, 88, 22, 36, 61. Найдены и другие точки, близкие по значению к оптимальным. График, построенный по найденным точкам в координатах (C, χ), имеет вид ломаной линии, однако показывает близкую к линейной зависимость. Аппроксимирующая линия пересекает значение χ = 1 в точке теоретического минимума около C = 2877210. Расписание для C = 2877210 может и не существовать, лишь только для больших значений.
Следовательно, значения, находимые методом мультистарта на основе АОПО, близки к теоретически минимальным. Ранее бессистемно было найдено значение Cmin = 2877250 (χ = 0,9999939412). Новый предлагаемый метод позволяет находить в среднем C = 2877242,8 (интерполируя, получено χ = 0,9999949726). Следовательно, среднее χ на 17 % ближе к теоретическому минимуму, чем для найденного ранее значения, а χ для нового Cmin – соответственно на 47 %.
Заключение
Для того чтобы параметры АОПО были оптимальны, при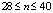 
нужно использовать метод мультистарта при 
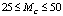, схему Коши при DS = 100, оптимальный алгоритм сортировки, значения R = 4, X = 2. Для определения номера оптимального алгоритма сортировки требуется запускать алгоритмы с 1 по 34 и выбирать алгоритм с минимальным результатом. Для этого требуется 12 с процессорного времени, что несущественно по сравнению со временем оптимизации.