Электромембранные технологии в настоящее время считаются критически важными технологиями. Они используются для решения таких актуальных проблем, как создание безотходных технологий, включая очистку сточных вод, например, гальвонического производства, содержащих ионы тяжелых металлов (цинк, свинец, кадмий и др.) [1]. Важнейшей проблемой являяется очиска воды от радиоактивных изотопов. Электромембранные технологии могут быть использованы для дезактивации воды, если радиоактивные вещества находятся в ней в растворенном состоянии в виде ионов, например для дезактивации слабоминерализованных сбросных вод ядерных реакторов, воды контурного охлождения. При этом требуется ее глубокое обессоливание. Одной из наиболее важных интегральных характеристик переноса ионов соли в мембранных системах является вольт-амперная характеристика (ВАХ), которая применяется при разработке оптимальной конструкции и выборе технологического режима работы, оценке соответствия теоретических и экспериментальных ВАХ [2, 3]. Именно используя ВАХ, вводятся фундаментальные понятия таких критических плотностей токов, как предельная, экзальтационная и Харкаца, и так далее [1]. В работе выведено новое уравнение, заменяющее уравнение Пуассона, позволяющее построить математическую модель переноса и алгоритм расчета вольт-амперной характеристики для произвольной соли в гальванодинамическом режиме. Статья является продолжением и обобщением результатов работы [4] на общий случай произвольной соли.
Рассмотрим отдающий диффузионый слой (ДС). Пусть H – ширина диффузионного слоя, x = 0 соответствует глубине раствора, где выполняется условие локальной электронейтральности, а x = H – границе ионообменная мембрана/раствор.
Перенос ионов произвольной соли в ДС в потенциодинамическом режиме, описывается уравнениями [2, 4]:
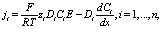 (1)
(1)
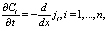 (2)
(2)
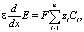 (3)
(3)
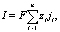 (4)
(4)
где 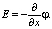
В связи с тем, что уравнение Пуассона (3) позволяет вычислить значение потенциала, то (1)–(3) используется для моделирования переноса в потенциодинамическом режиме [2]. Нашей целью является вывод дифференциального уравнения для плотности тока, которая должна заменить уравнение (3), формулы и алгоритма расчета ВАХ.
Материалы и методы исследования
Путем тождественных преобразований из (1)–(4) выводятся:
1) формула для вычисления E, которое заменяет формулу (4) для вычисления I;
2) новое дифференциальное уравнение для I.
В итоге получаем математическую модель переноса ионов произвольной соли в гальванодинамическом режиме.
На основе этой модели разработан алгоритм численного расчета теоретической вольт-амперной характеристики. Рассмотрены упрощения, которые возможны в частных случаях стационарного переноса, а также при выполнении условия локальной электронейтральности. Показано, что в этих частных случаях уравнения совпадают с уравнениями из работ [4–6], что свидетельствует об адекватности результатов работы.
Результаты исследования и их обсуждение
1. Преобразование (1)–(4)
1) Вывод формулы для вычисления I.
Из (1) и (4) имеем
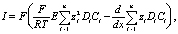
следовательно (см. [2]):
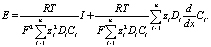 (5)
(5)
Обозначим
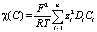 , RОм(C) = 1/χ(C),
, RОм(C) = 1/χ(C),
тогда получим
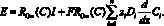 (6)
(6)
Заметим, что RОм(C) проводимость раствора [2].
2) Вывод нового дифференциального уравнения для I.
Подставим (6) в уравнение Пуассона (3), тогда получим уравнение для плотности тока I:
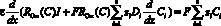
или
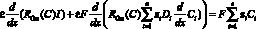
или
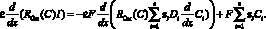 (7)
(7)
3) Преобразование уравнений (1), (2).
Дифференцируем (1) по x и получим
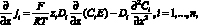
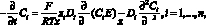
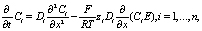
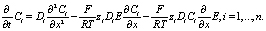
Заменим 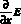 исходя из (3):
исходя из (3):
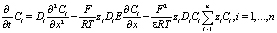
или
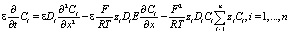
Откуда
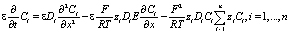 (8)
(8)
или
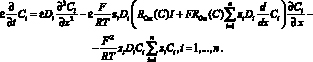 (9)
(9)
Уравнение (9) – это нелинейное параболического типа дифференциальное уравнение для парциальных концентраций Ci, зависящее еще и от плотности тока I.
В итоге получили систему уравнений (7), (8), (9) для Ci, ji, i = 1,..., n, I. Она позволяет вместе с соответствующими краевыми условиями однозначно определить Ci, ji, i = 1,..., n, I и являются математической моделью переноса произвольной соли в гальванодинамическом режиме.
4) Алгоритм расчёта ВАХ.
а) Задается некоторый темп роста α функции I(t, H), начиная с некоторого значения I0: 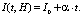
б) Решается (7), (8) с соответствующими граничными условиями и I(t, x) и Ci, i = 1,..., n.
в) Рассчитывается E по формуле (6).
г) Находится скачок потенциала по формуле 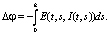
2. Упрощение модели в стационарном случае
Рассморим стационарный перенос произвольной соли в гальваностатическом режиме. В этом случае потоки постоянны:
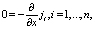
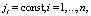
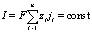
поэтому алгоритм рсчета ВАХ становится проще.
Алгоритм расчета ВАХ
а) Задается набор значений Il, l = 1,..., m.
б) Решается уравнение (6) с соответствующими краевыми условиями и I = Il, находятся Ci, i = 1,..., n.
в) Определяем E:
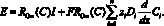
г) Определяем скачок потенциала по формуле 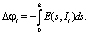
Набор 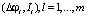 представляет собой вольт-амперную характеристику.
представляет собой вольт-амперную характеристику.
3. Упрощение модели при выполнении условия электронейтральности 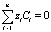
Прт выполнения условия 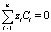 уравнения (1), (2), (6), (7) упрощается, так как I не зависит от x, хотя потоки могут зависит от x. Действительно, из (2) следует
уравнения (1), (2), (6), (7) упрощается, так как I не зависит от x, хотя потоки могут зависит от x. Действительно, из (2) следует
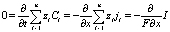
или
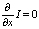 , т.е. I = I(t)
, т.е. I = I(t)
где I(t) задается.
Кроме того, соотношение 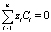 позволяет найти одну из концентраций если известны
позволяет найти одну из концентраций если известны 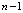 концентрации, например если известны Ci, i = 1,..., n – 1, то
концентрации, например если известны Ci, i = 1,..., n – 1, то 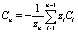 . Следовательно, число уравнений для определения концентраций должно быть n – 1, поэтому из (6) получаем
. Следовательно, число уравнений для определения концентраций должно быть n – 1, поэтому из (6) получаем
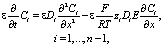 (10)
(10)
где E определяется по формуле (6).
Уравнение (7) выполняется тождественно.
Алгоритм расчета ВАХ
а) Задается некоторый темп роста α плотности тока I(t), начиная с некоторого значения I0: 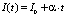 .
.
б) Решается система уравнений (10) и определяется Ci, i = 1,..., n – 1, затем вычисляется Cn по формуле 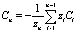 .
.
в) Рассчитывается напряженность электрического поля по формуле (6).
г) Находится скачок потенциала по формуле 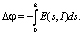
4. Упрощение модели п. 3 для бинарного электролита
Для бинарного электролита, можно ввести эквивалентную концентрацию C: 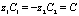 , тогда из (10) получаем
, тогда из (10) получаем
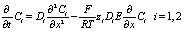
или с использованием эквивалентной концентрации получим
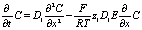 ,
,
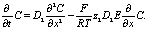
Откуда следует
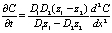
или
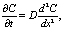 (11)
(11)
где 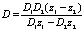 – коэффициент диффузии электролита [1, 2].
– коэффициент диффузии электролита [1, 2].
Вычислим
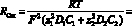
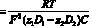 ,
,
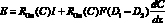
или
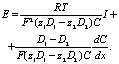 (12)
(12)
Вычислим j1 и j2 потоки. Несложно показать
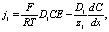 (13)
(13)
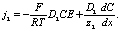 (14)
(14)
Алгоритм расчета ВАХ
а) Задается некоторый темп роста α плотности тока I(t), начиная с некоторого значения I0: 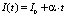 .
.
б) Из (11) находим С, и затем 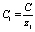 ,
, 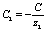 .
.
в) Рассчитываются потоки по формулам (13), (14).
г Рассчитывается E по формуле (12).
д) Находится скачок потенциала по формуле 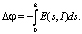
В работе выведено новое уравнение для плотности тока, построена математическая модель и разработан алгоритм расчета вольт-амперной характеристики для переноса произвольной соли в гальванодинамическом режиме. Для стационарного переноса или при выполнении условия локальной электронейтральности, уравнения математической модели и алгоритм расчета ВАХ существенно упрощаются. Особенно они упрощаются для бинарной соли. В этом частном случае результаты совпадают с аналогичным частным случаем математических моделей переноса бинарной соли в диффузионном слое из работы [4], что свидетельствует об адекватности предложенных в работе моделей переноса и алгоритма расчета ВАХ
Заключение
Предложенные в работе математические модели и алгоритм расчета ВАХ могут служить математическим инструментом для теоретического исследования переноса ионов произвольной соли в приборах и устройствах, использующих ионообменные мембраны.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта 19-08-00252 А «Теоретическое и экспериментальное исследование вольт-амперных характеристик электромембранных систем».



