В настоящее время быстрые преобразования Фурье (БПФ) нашли широкую реализацию в беспроводных системах связи, построенных на основе технологии OFDM. Применение прямого и обратного БПФ позволяет обеспечивать эффективное использование радиочастотного диапазона при заданных скоростях передачи информации, борьбу с многолучевостью и межсимвольной интерференцией. Однако ортогональные преобразования на основе БПФ имеют недостаток, который приводит к значительным погрешностям вычислений [1]. Для устранения такого недостатка в работах [2–4] предлагается использовать целочисленные ортогональные преобразования сигналов. С целью повышения скорости их выполнения в работах [4–6] предлагается использовать непозиционные модулярные коды (НМК). В кодах НМК отсчеты обрабатываемого сигнала и ортогональные коэффициенты представляются в виде набора остатков, что позволяет реализовать параллельные вычисления. Кроме того, такие арифметические коды способны проводить поиск и коррекцию ошибок вычислений. Для этого в НМК вводят дополнительные избыточные модули. Поэтому разработка алгоритма, позволяющего повысить достоверность обработки сигналов при возникновении сбоев и отказов в работе устройства OFDM, является актуальной задачей.
Для повышения эффективности выполнения целочисленных ортогональных преобразований сигналов целесообразно использовать непозиционные модулярные коды. Благодаря тому, что операнды имеют маленькую разрядность, а остатки получаются независимо друг от друга, то арифметические операции выполняются значительно быстрее, чем в позиционной системе счисления (ПСС) [5–7]. Непозиционные модулярные коды способны обнаруживать и корректировать ошибки, возникающие в процессе обработки данных. Для этого необходимо увеличить их избыточность за счет добавления дополнительных модулей. Однако это приводит к увеличению схемных затрат, что снижает эффективность использования беспроводных систем передачи информации. Поэтому целью работы является разработка алгоритма, позволяющего обнаружить и исправить ошибку в НМК при минимальных схемных затратах.
Материалы и методы исследования
Обеспечение реального масштаба времени при выполнении ортогональных преобразований сигналов возможно за счет использования параллельных вычислений. В работах [4–6] представлены математические модели выполнения таких преобразований, реализованные с использованием непозиционных модулярных кодов. Такие коды являются арифметическими, поэтому их можно использовать для поиска и коррекции ошибок, которые имеют место при вычислениях из-за сбоев. В таких кодах позиционный код числа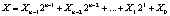 
, где 
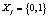, j = 0,…, n – 1, сначала представляют в виде полинома
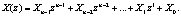(1)
Затем выбирается множество взаимно простых полиномов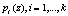 
. Для получения НМК необходимо вычислить остатки 
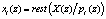. Тогда справедливо
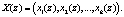(2)
Набор выбранных оснований определяет рабочий диапазон НМК
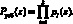(3)
Так как остатки получены независимо друг от друга, то для двух комбинаций НМК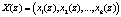 
и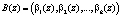 
справедливы выражения
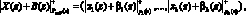(4)
(5)
Так как в основе ортогональных преобразований сигналов лежат аддитивные и мультипликативные операции, тогда их математическая модель, реализованная в непозиционных модулярных кодах, имеет вид
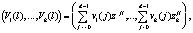(6)
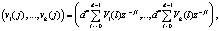(7)
где z – элемент поля, порожденного полиномом pi(z);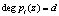 
; 
; 
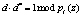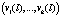– набор отсчетов входного сигнала; 
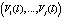– вектор спектральных составляющих сигнала; 
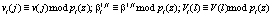; j = 1, …, d – 1.
Чтобы произвести коррекцию ошибок, возникающих из-за сбоев в процессе реализации вычислений, в непозиционные модулярные коды необходимо добавить избыточные основания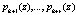 
. При этом должно выполняться условие
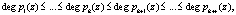(8)
где r – количество избыточных оснований.
Это приводит к расширению рабочего диапазона НМК до полного, который равен
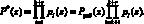(9)
Для расширенной комбинации кода НМК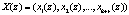 
должно выполняться равенство
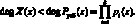(10)
В случае возникновения однократной ошибки в i-м остатке, получаем
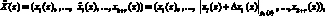(11)
где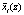 
– искаженный остаток комбинации; 
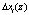– глубина однократной ошибки.
В результате искажения комбинации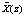 
выйдет за пределы Pраб(z), так как
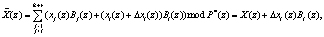(12)
где Bj(z) – ортогональный базис для j-го основания НМК.
Таким образом, очевидно, что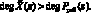 
Согласно [6] для коррекции ошибки, искажающей только один остаток НМК, необходимо использовать два контрольных основания, удовлетворяющих условию
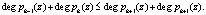(13)
Так как НМК являются непозиционными кодами, то для коррекции ошибки необходимо сравнить степени числа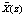 
и Pраб(z). В работе [6] для этого предлагают использовать интервал полинома, который определяется
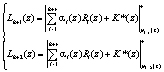, (14)
где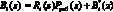 
; B*j(z) – ортогональный базис НМК без контрольных оснований; 
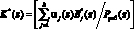– ранг безызбыточного НМК.
Проведенные исследования показали, что данный алгоритм является избыточным. Устранить данный недостаток позволяет разработанный алгоритм, в котором используется синдром ошибки по контрольным основаниям НМК. Для его вычисления необходимо выполнить следующие вычисления:
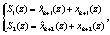(15)
где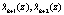 
– остатки, которые вычислены с помощью информационных остатков.
Если синдром ошибки является нулевым, а это возможно при совпадени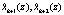и 
и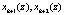 
, то код НМК является разрешенным. В противном случае очевидно, что комбинация НМК содержит ошибку.
Анализ выражения (12) показал, что только второе слагаемое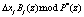 
определяется искаженным остатком. Осуществим перевод из НМК, определяемого только рабочими основаниями 
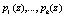, в позиционный код. Тогда имеем
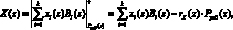(16)
где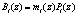 
– ортогональный базис НМК; mi(z) – вес базиса Bi(z); 
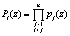; rX(z) – ранг кода X(z), показывающий число превышений Pраб(z).
Используя требование ортогональности базисов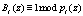 
, найдем произведение остатков НМК на величину веса базиса Bi(z). Тогда получаем, что данное произведение удовлетворяет условию 
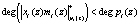. В этом случае степень произведения 
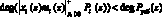. Учитывая, что суммирование производится по модулю два, то выражение (16) преобразуется к виду
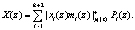(17)
Тогда для вычисления первого контрольного остатка необходимо выполнить
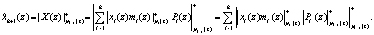(18)
Второй остаток по контрольному основанию определяется
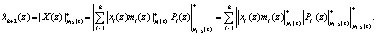(19)
Затем остатки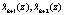 
суммируются по модулю два с остатками 
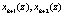, входящими в комбинацию 
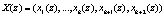. Полученное значение синдрома ошибки укажет на наличие ошибки в НМК.
Результаты исследования и их обсуждение
Пусть заданы информационные основания НМК,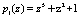 
, 
, 
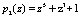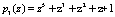. В этом случае рабочий диапазон составит 
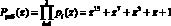. Для коррекции однократной ошибки введем два контрольных основания 
, 
.
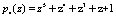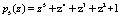Вычислим значение констант Pi(z) информационных оснований и весов mi(z) ортогональных базисов определяются из условия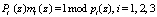 
:
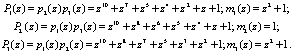
Представим значение констант Pi(z) контрольным основаниям
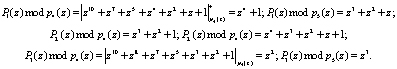
Пусть задан полином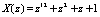 
, который удовлетворяет условию (10). Представим данный полином в НМК 
.
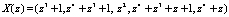Для вычисления первого контрольного остатка воспользуемся (18). Тогда
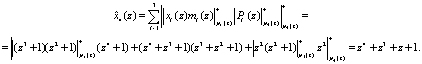
Второй остаток по контрольному основанию определяется выражением (19)
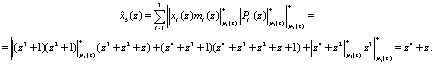
Для вычисления синдрома ошибки воспользуемся (15). Тогда получаем
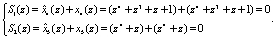
Так как синдром ошибки равен нулю, то X(z) является разрешенной комбинацией.
Пусть ошибка произошла в третьем остатке, а ее глубина равна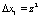 
. Тогда ошибочная комбинация имеет вид 
.
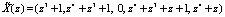Вычислим первый контрольный остаток:
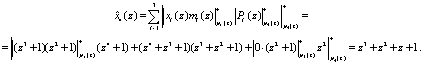
Второй остаток по контрольному основанию определяется выражением (19):
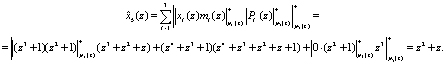
Для вычисления синдрома ошибки воспользуемся (15). Тогда получаем
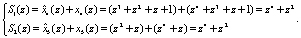
Так как синдром ошибки не равен нулю, то комбинация НМК X(z) содержит ошибку.. В рассмотренном примере получаем вектор ошибки, который имеет вид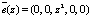 
. Для устранения ошибки необходимо сложить комбинацию 
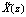с вектором ошибки. Получаем
.
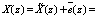
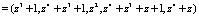На основе разработанного алгоритма была получена структурная модель блока обнаружения и коррекции ошибки. В каждом контрольном основании необходимы три LUT-таблицы для выполнения операции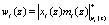 
, три LUT-таблицы для выполнения процедуры 
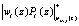, где j = 1, 2, а также две LUT-таблицы для вычисления 
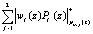. Полученные результаты свидетельствуют о том, что для рассмотренного примера потребуется 16 LUT-таблиц.
В алгоритме поиска и коррекции ошибок на основе выражения (14) в каждом контрольном канале потребуется пять LUT-таблиц для выполнения операции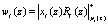 
, i = 1,…, 5, четыре LUT-таблицы для вычисления суммы wi(z). Кроме того, для вычисления ранга безызбыточного НМК K*(z) необходимо пять LUT-таблиц. Таким образом, схемная реализация требует 23 LUT-таблицы. Следовательно, использование разработанного алгоритма поиска и коррекции ошибок позволяет снизить схемные затраты в 1,44 раза по сравнению с алгоритмом, приведенным в работе [6].
Заключение
Для повышения скорости выполнения ортогональных преобразований сигналов в системах OFDM предложено использовать НМК, так как в данных кодах отсчеты обрабатываемого сигнала и ортогональные коэффициенты представляются в виде остатков, над которыми выполняется параллельное вычисление. Показано, что применение НМК позволяет проводить поиск и коррекцию ошибок вычислений. В статье представлен разработанный алгоритм, позволяющий повысить достоверность обработки сигналов при возникновении сбоев и отказов в работе устройства OFDM. При этом для его реализации требуется в 1,44 раза меньше схемных затрат по сравнению с алгоритмом, приведенным в работе [6] уже при использовании пятиразрядных модуле НМК.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-37-00009.