Современные всемирные взгляды, тенденции образования способствовали принятию иных стандартов образования в России. В Федеральном государственном образовательном стандарте одним из основных требований к результатам освоения основной образовательной программы определяется развитие и саморазвитие личности обучающихся на основе формирования УУД. Таким образом, основной целью современного образования становится развитие у учащихся способности самостоятельно усваивать новые знания, проектировать пути и способы реализации, поставленной цели, а в дальнейшем контролировать и критично оценивать процесс своей деятельности.
Цель исследования: обозначить методические приемы, которые будут содействовать формированию регулятивных универсальных учебных действий в процессе обучения математике.
Материалы и методы исследования
Материалом исследования стала научная, научно-методическая литература, в которой особого внимания заслуживает проблема формирования регулятивных универсальных учебных действий, а также собственный педагогический опыт. В качестве методов использовались теоретический анализ, анализ психолого-педагогической и методической литературы, изучение, систематизация и обобщение материалов по данной проблеме.
Результаты исследования и их обсуждение
Проблемы разработки системы обучения, при которой достигался бы более значительный уровень развития, чем при обучении по устоявшимся методикам, рассматривались еще в далекие 1960-е гг. научным коллективом под руководством Л.В. Занкова. Они подчеркивали важность создания основы для всестороннего гармонического развития учащихся в начальной школе, построенного на принципах осмысления взаимосвязи и систематизации изучаемого материала, личностной рефлексии и саморегуляции с учетом индивидуальных особенностей учащихся [1, c. 16–17].
С.Л. Рубинштейн, изучая психические явления и их внутренние взаимосвязи, писал, что для их понимания «нужно прежде всего найти ту «клеточку», или «ячейку», в которой можно вскрыть зачатки всех элементов психологии в их единстве». «...Такой клеточкой является любое действие, как... единица деятельности» [2, c. 192–193].
Н.Ф. Талызина [3, c. 7] писала: «Образ всегда есть результат, продукт определенных действий. Восприятие как чувственный образ – результат действий восприятия, продукт «воспринимания»». И выделила, что при этом ведущая роль принадлежит действию.
Постепенно педагоги ученые пришли к выводу, что знания невозможно получить без действий, поэтому учителю необходимо иметь представления о видах действий и о том, как их формировать.
Далее Ю.К. Бабанским была разработана классификация основных умений и навыков учебного труда (общеучебных умений и навыков), соответствующей не только структуре деятельности, но и процессу усвоения знаний, который состоит из таких элементов, как принятие цели, мотивации усвоения, восприятие, осмысление и оперирование учебной информацией, самоконтроль и анализ результатов освоения. Таким образом, владение совокупностью основных умений и навыков учебного труда характеризует умение рационально учиться.
К сожалению, понимая важность развития общеучебных умений учащихся, долгое время в системе российского образования всерьёз их формированием были озадачены только представители развивающего обучения во главе с В.В. Давыдовым и Д.Б. Элькониным. Лишь в 2004 г. в Федеральном компоненте образовательного стандарта начального общего образования как преимущество указывается формирование общеучебных умений и навыков и только в 2012 г. был принят Федеральный государственный образовательный стандарт, методологической основой которого является системно-деятельностный подход, предполагающий формирование готовности обучающихся к саморазвитию и непрерывному образованию. Требования к результатам освоения основной образовательной программы стандарт отражены в личностных, метапредметных и предметных результатах. К метапредметным относится освоение универсальных учебных действий. Сформированные у учащихся универсальные учебные действия должны дать им возможность самостоятельно осуществлять учебную деятельность, способствовать их саморазвитию и самосовершенствованию, создавать основу для дальнейшей самореализации учащихся как личности, положительно влиять на успешность достижения образовательных результатов [4].
В данной статье остановимся на формировании регулятивных УУД. И, прежде всего, разберемся со значением слова «регулятивный». Регулятивный – определяющий направление, развитие чего-нибудь, вносящий порядок, планомерность во что-нибудь [5]. Иммануил Кант под регулятивным понимал принцип разума, который регулирует только созерцание, мышление и направляет к познанию [6].
По мнению авторского коллектива под руководством А.Г. Асмолова, регулятивные действия можно определить как совокупность способов действия учащегося, обеспечивающих самостоятельное усвоение новых знаний, формирование умений, включая организацию этого процесса. Таким образом, регулятивные универсальные учебные действия призваны обеспечивать не только регуляцию, но и организацию и коррекцию учебной деятельности. Исследуя особенности формирования регулятивных УУД, мы пришли к выводу, что суть их формирования заключается в том, что учащийся должен владеть отдельными компонентами каждого действия. Далее рассмотрим компоненты действий регулятивных УУД.
1. Целеполагание: Смотивировать учащихся на временную перспективу ⇒ определить границы знания и незнания выбранной темы ⇒ формулировать устно и письменно цель деятельности ⇒ обосновать значения цели для решения учебных и жизненных потребностей ⇒ конкретизировать цели до поэтапного выполнения ряда задач ⇒ выделить способы и средства достижения цели ⇒ соотносить цели с конечным результатом.
2. Планирование. Сформировать мотивационную основу действия ⇒ составить схему ориентировочной основы действия ⇒ сформировать действия в материализованной форме ⇒ оформить действия в громкой речи (действие с «проговариванием») ⇒ формировать действия во внутренней речи «про себя» ⇒ формирование действия во внешней речи ⇒ составить план действий процесса решения учебной задачи с учетом расходования времени ⇒ соотнести поставленную цель с конечным результатом ⇒ анализировать выполнение плана ⇒ внести исправления и дополнения в план в случае изменения условий.
3. Прогнозирование. Прогнозировать конечный результат работы ⇒ прогнозировать этапы решения учебной задачи для достижения конечного результата с учетом расходования времени ⇒ прогнозировать возможные трудности для достижения конечного результата (ошибкоопасных моментов).
4. Контроль. Сопоставлять собственные действия с образцом действия ⇒ сопоставлять полученный результат с образцом ⇒ анализировать и учитывать условия выполнения действия.
5. Коррекция. Обозначить индивидуальные пути преодоления индивидуальных трудностей ⇒ вносить изменения (коррективы) в план действий достижения конечного результата с учетом индивидуальных затруднений.
6. Оценка. Выделять критерии оценки деятельности (учителем самостоятельно или в совместной договоренности учителя с учащимися) ⇒ осознавать то, что уже усвоено, а что подлежит дальнейшему повторению ⇒ осознавать уровень качества освоения способа ⇒ выделять достижения поэлементно (выделение отдельных элементов знаний и умений, оценивание их поэлементно) ⇒ выделять трудности при изучении темы ⇒ выделять причины неудач при выполнении работы.
7. Волевая саморегуляция. Мобилизовать силы и энергию учащихся ⇒ преодолевать препятствия, возникающие в ходе выполнения действий.
Далее рассмотрим некоторые примеры методических приемов формирования регулятивных универсальных учебных действий на уроках математики.
Приемы формирования целеполагания. Прием «Задай вопрос». В начале изучения темы «Площадь поверхности цилиндра» можно задать следующее задание: Даны две жестяные банки цилиндрической формы. Первая банка в два раза шире второй, а вторая вдвое выше первой. Для того чтобы этот текст стал задачей, добавьте к этому условию вопрос.
В 6 классе на этапе актуализации темы «Сложение чисел с помощью координатной прямой» можно использовать стандартный прием «Удивляй». Проводится фронтально. Ответьте на вопросы: 1) Как изменился бы климат Якутии, если бы температура воздуха повысилась на 30 градусов (зимой и летом)? 2) Как бы изменилась территория села Техтюр, если бы уровень озера Туора-Кюель повысился на 80 метров? (использование физической карты Мегино-Кангаласского улуса).
В 8 классе (целеполагание как постановка учебной задачи уже известного и еще неизвестного) при изучении теоремы Виета раздаются листы с заданием заполнить таблицу. После заполнения ученики замечают связь между корнями уравнений и произведением/суммой коэффициентов. Исходя из этого выявляют связь между коэффициентами квадратного уравнения и его корнями (рис. 1).
Рис. 1. Раздаточный лист с заданием
Приемы формирования действия прогнозирования. Прогнозирование ошибок. При изучении темы «Арифметический квадратный корень» перед решением задачи можно показывать ошибки, не дожидаясь, пока ученики их сделают.
На доске можно записать такую строчку: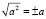 
. Затем распишем её поподробнее: 
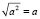или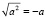 
. Теперь из первого равенства вычтем второе и получим 0 = 2a, откуда получаем, что a = 0.
Можно вместо а поставить конкретное значение, например, a = 2. Тогда получим, что 0 = 4. Потом уже объясняется смысл знака радикала и термина «арифметический корень».
При изучении темы «Степень с рациональным показателем» выпишем такую последовательность равенств:
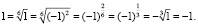
Здесь ошибка заключена в переходе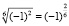 
, так как при определении степени с дробным показателем определены только для неотрицательных чисел.
Приемы формирования действия контроля. Задания-ловушки. Задания-ловушки могут быть разными: не имеющими решения, имеющими несколько решений, с лишними данными, с недостающими данными, с опережающим материалом. Например, при изучении темы «Объемы цилиндра» можно задать следующую задачу с недостающими данными по чертежу (рис. 2), с вопросом «Какую часть цилиндра вырезали?».
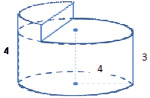
Рис. 2. Чертеж к задаче с недостающими данными
При изучении темы «Сокращение дробей» можно задать следующие вопросы: Можно ли «сократить» дробь: а)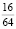 
, вычеркнув 6? б) 
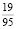, вычеркнув 9? в) 
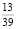, вычеркнув 3?
Суть данного приема заключается в том, чтобы научить контролировать условия задания, находить ошибки, определять границы знаний.
Прием «Шпаргалки». Содержание задачи дается на карточке. Задача ученика – передать содержание задачи с помощью рисунков, условных обозначений или схем. Закончив, отдает учителю. После всего этого ученикам раздаются шпаргалки, составленные другими учениками. По этой шпаргалке им нужно воспроизвести текст. Например, при изучении темы «Отрицательные и положительные числа» можно учащимся предложить следующие задачи, по которым нужно составить шпаргалки:
1. Высота возвышенности Дылбаахы в Мегино-Кангаласском улусе 92 м, а глубина озера Токур Кюель 8 м. Как можно выразить данные с помощью положительных и отрицательных чисел?
2. Село Техтюр находится на 25 м ниже уровня моря, а город Якутск на 20 м выше уровня моря. Как можно выразить данные с помощью положительных и отрицательных чисел?
3. В селе Техтюр Мегино-Кангаласского улуса была зафиксирована максимальная температура 32,8 °С и минимальная 52,2 °С. Как можно выразить данные с помощью положительных и отрицательных чисел?
4. Из истории аномальных ситуаций: В 2006 г. в городе Нерюнгри была зафиксирована температура 37 °С тепла, а в поселке Усть-Нера 72 °С холода. Как можно выразить данные с помощью положительных и отрицательных чисел?
Приемы формирования действия коррекции. Найди ошибку и объясни его причину. Например, ученик решил задачу «В параллелограмме АВCD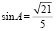 
. Найдите cos B» следующим образом: «Известно, что 
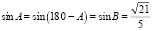. Значит, синусы двух любых соседних углов параллелограмма равны. Теперь найдем cos B из тождества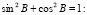 
.»
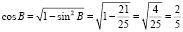В чём допускает ошибку ученик? Перед квадратным корнем упускают знак «плюс» или «минус» и получают неотрицательное число. Это происходит из-за того, что здесь решается геометрическая задача и при использовании основного тригонометрического тождества, например при решении прямоугольного треугольника в курсе геометрии основной школы перед корнем всегда стоит плюс, так как в прямоугольном треугольнике углы острые, поэтому и значения тригонометрических функций углов положительны и учащиеся настолько привыкают к этому, что это как-то отпечатывается в сознании.
При изучении темы «Квадратичная функция» можно учащимся предложить следующее задание: «Найдите наибольшее и наименьшее значение функции y = x2 – x + 1, где x? [2; 3].
«Решение Айааны». Так как 2 ≤ x ≤ 3, то 4 ≤ x2 ≤ 9. Также получим –2 ≤ –x ≤ –3. Откуда, складывая получившиеся неравенства и прибавляя 1, получим, что 3 ≤ x2 – x + 1 ≤ 7.
Ответ: Наименьшее значение функции равно 1, наибольшее – 7.
«Решение Айсена». На промежутке [2; 3] функция y = x2 – x + 1 возрастает, а потому f(2) ≤ y ≤ f(3), т.е. 3 ≤ y ≤ 7.
Ответ: Наименьшее значение функции равно 3, наибольшее – 7.
Являются ли решения верными? Какие есть ошибки? Объясните ошибки и недочеты в представленных решениях.
Для выявления объективной причины ошибок, учащимся предлагается проанализировать, сделать «маленькое исследование» причины ошибки. Анализируя причины ошибок, школьники учатся восстанавливать ход своей мысли и находить место ошибки.
Кроме этого можно использовать следующие задания:
- задайте вопрос к выступавшему у доски;
- выскажите замечания по тому, что сказано или написано;
- придумайте софистическую ошибку.
Заключение
Мы считаем, что применение различных методических приемов формирования регулятивных универсальных учебных действий будет способствовать развитию умения ставить конкретные жизненно-практические цели, расставлять приоритеты и планировать свою жизнь, оценивать текущую ситуацию и прогнозировать ее развитие и тем самым открывает возможность выбора успешных стратегий в различных ситуациях, успешного существования в современном обществе, используя всевозможные ресурсы для достижения поставленных целей и реализации жизненных планов.