Одним из основных составных частей помехозащищенности низкоорбитальных систем спутниковой связи (НССС) является обеспечение информационной скрытности [1–3]. Очевидно, что информационная скрытность задается способностью НССС противостоять деструктивным воздействиям, которые направлены на извлечение информации из передаваемых по каналам связи сигналов. В этом случае раскрытия смысла передаваемой информации связано с отождествлением каждой совокупности принятого сигналов с содержание сообщения [4]. Одним из наиболее эффективных методов, позволяющих повысить информационную скрытность НССС, является использование систем шифрования. В настоящее время создано значительное количество различных алгоритмов криптографической защиты. Особое место среди таких методов занимают алгоритмы нелинейные шифрования (НШ), в которых используется совокупность мультипликативных и аддитивных операций в конечных полях Галуа. Реализация метода защиты информации на основе совокупности операций по модулю в конечном поле Галуа приводит к повышению информационной скрытности НССС. Поэтому разработка метода нелинейного шифрования данных на основе процедуры возведения в степень для поля Галуа является актуальной задачей.
Современные низкоорбитальные системы спутниковой связи должны обладать высокой информационной скрытностью. По мере увеличения трафика передаваемых данных и повышения скорости передачи информации особое внимание приобретают методы поточного шифрования. Однако, обеспечивая высокую скорость закрытия информации, поточные шифры, построенные на основе сложения по модулю два потока открытых данных с шифрующей гаммой, представляющей собой набор псевдослучайных символов, не обладают достаточной информационной стойкостью. Это связано с тем, что обратная функция шифрования базируется на выполнении одной аддитивной операции. Устранить данный недостаток позволяют методы нелинейного шифрования. Однако не все они обладают достаточной производительностью. Поэтому цель статьи – повысить скорость выполнения нелинейного шифрования данных за счет реализации операции возведения в степень в полях Галуа.
Материалы и методы исследования
Информационная скрытность низкоорбитальной системы спутниковой связи во многом определяется степенью защищенности информации от случайных и преднамеренных воздействий нарушителей. Такие деструктивные воздействия могут привести к значительному ущербу субъектам, которые являются владельцами передаваемой по НССС информации. Для устранения данного недостатка широко используются методы шифрования. Особое место занимают поточные системы шифрования, так как обеспечивают достаточно высокую скорость зашифрования [5]. В качестве генератора шифрующей гаммы в таких системах предлагается использовать генераторы, вырабатывающие псевдослучайную последовательность. В работах [5–7] показаны методы и схемные решения систем поточного шифрования, которые реализуются с использованием целочисленных алгебраических систем на основе регистров сдвига с линейной обратной связью. При этом поточный шифр, построенный на основе модульной операции сложении потока псевдослучайных битов, полученных с помощью многотактных кодовых фильтров, с битами потока открытых данных теоретически имеет высокую информационную скрытность. Однако такие системы имеют недостаток – недостаточная криптостойкость из-за возможности вскрытия при наличии определенного числа символов открытого текста и соответствующему ему зашифрованного текста.
Устранить отмеченный недостаток позволяют методы нелинейного шифрования, которые эффективно реализуются в конечных полях Галуа. В отличие от поточного шифрования, в котором прямое и обратное криптопреобразование выполняется с помощью одной операции, методы нелинейного шифрования имеют более широкие возможности по обеспечению информационной скрытности передаваемых данных [8]. Это связано с тем, что в таких системах НШ используются преобразования, реализующие как отдельные аддитивные и мультипликативные операции, так и их различные комбинации В качестве примера можно представить следующие методы НШ
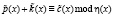 , (1)
, (1)
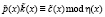 , (2)
, (2)
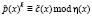 , (3)
, (3)
где 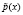 – полиномиальная форма блока открытых данных длиной L разрядов;
– полиномиальная форма блока открытых данных длиной L разрядов; 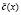 – полиномиальная форма блока зашифрованных данных длиной L разрядов;
– полиномиальная форма блока зашифрованных данных длиной L разрядов; 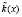 – полиномиальная форма ключа длиной L разрядов;
– полиномиальная форма ключа длиной L разрядов; 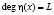 – степень порождающего полинома η(x) – множество ключевых данных.
– степень порождающего полинома η(x) – множество ключевых данных.
Рассмотрим метод нелинейного шифрования, реализуемый в поле Галуа, который в своей основе имеет метод возведения в степень элементов 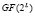 . Для реализации данного метода необходимо использовать неприводимый полином η(x). На основе данного полинома порождаются ненулевые элементы мультипликативной группы. Если положить, что степень порождающего полинома равна L, то входной поток открытых данных необходимо разделить на блоки длиной L бит. Тогда полиномиальная форма полученного блока открытых данных имеет вид
. Для реализации данного метода необходимо использовать неприводимый полином η(x). На основе данного полинома порождаются ненулевые элементы мультипликативной группы. Если положить, что степень порождающего полинома равна L, то входной поток открытых данных необходимо разделить на блоки длиной L бит. Тогда полиномиальная форма полученного блока открытых данных имеет вид
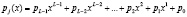 , (4)
, (4)
где 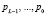 – двоичные разряды j-го блока открытых данных;
– двоичные разряды j-го блока открытых данных; 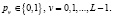
Таким образом, для j-го блока, представленного в полиномиальной форме в виде многочлена pj(x), справедливо
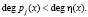 (5)
(5)
В этом случае данный блок, длиной L двоичных разрядов, считается элементом 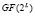 . Для реализации процедуры шифрования на основе возведения в степень элемента расширенного поля Галуа вычисляются значения псевдослучайной последовательности X. Если обеспечить устранение блока, состоящего из L нулей, то ключевую последовательность, представляющую собой ПСП, можно записать в виде кортежа ненулевых числе
. Для реализации процедуры шифрования на основе возведения в степень элемента расширенного поля Галуа вычисляются значения псевдослучайной последовательности X. Если обеспечить устранение блока, состоящего из L нулей, то ключевую последовательность, представляющую собой ПСП, можно записать в виде кортежа ненулевых числе
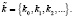 (6)
(6)
Тогда зашифрование потока данных для j = 0, 1, …. будет выполняться согласно
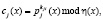 (7)
(7)
где cj(x) – j-й блок зашифрованных данных, представленный в полиномиальной форме;
Процедура расшифрования потока на приемной стороне является обратной задачей уравнения (7). Тогда для получения j-й блока открытых данных необходимо реализовать
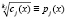 . (8)
. (8)
Для получения ключевой последовательности 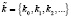 можно использовать многотактовые кодовые фильтры, построенные на основе регистров сдвига. Так как операция возведения в степень элементов конечного поля реализуется по модулю порождающего полинома η(х), то для повышения скорости выполнения данной процедуры целесообразно использовать быстрый алгоритм возведения в степень. Согласно [крипт] на данную итерацию зашифрования потребуется не более
можно использовать многотактовые кодовые фильтры, построенные на основе регистров сдвига. Так как операция возведения в степень элементов конечного поля реализуется по модулю порождающего полинома η(х), то для повышения скорости выполнения данной процедуры целесообразно использовать быстрый алгоритм возведения в степень. Согласно [крипт] на данную итерацию зашифрования потребуется не более 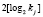 операций умножений. Если считать, что j-й блок ключевой последовательности удовлетворяет условию
операций умножений. Если считать, что j-й блок ключевой последовательности удовлетворяет условию
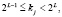 (9)
(9)
то очевидно, что 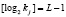 . Таким образом, очевидно следующее противоречие. Для обеспечения высокой информационной скрытности НССС необходимо увеличивать порядок конечного поля Галуа. Но при этом происходит снижение скорости выполнения шифрования. Устранить данное противоречие позволит разработанный метод нелинейного шифрования информации с использованием операции возведения в степень в сумме полей Галуа. Такой переход от шифрования блока данных pj(x) длиной L бит, к параллельному шифрованию блоков меньшей длины
. Таким образом, очевидно следующее противоречие. Для обеспечения высокой информационной скрытности НССС необходимо увеличивать порядок конечного поля Галуа. Но при этом происходит снижение скорости выполнения шифрования. Устранить данное противоречие позволит разработанный метод нелинейного шифрования информации с использованием операции возведения в степень в сумме полей Галуа. Такой переход от шифрования блока данных pj(x) длиной L бит, к параллельному шифрованию блоков меньшей длины 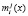 позволяет повысить скорость шифрования. Это обусловлено изоморфизмом китайской теоремы об остатках (КТО).
позволяет повысить скорость шифрования. Это обусловлено изоморфизмом китайской теоремы об остатках (КТО).
В этом случае используется сумма конечных полей Галуа, имеющая вид
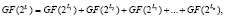 (10)
(10)
где 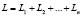 .
.
Для реализации разработанного метода нелинейного шифрования с использованием операции возведения в степень в сумме конечных полей Галуа необходимо разбить исходный блок pj(x) длиной L бит согласно
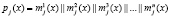 , (11)
, (11)
где || – операция конкатенация; 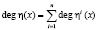 ; ηi(х) – порождающий полином конечного поля Галуа
; ηi(х) – порождающий полином конечного поля Галуа 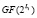 ; Li = deg ηi(х).
; Li = deg ηi(х).
Тогда процесс зашифрования описывается выражением
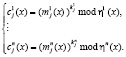 (12)
(12)
Процедура расшифрования в сумме конечных полей Галуа будет определяться
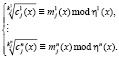 . (13)
. (13)
Если в выбранном наборе конечных полей справедливо 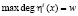 , то при использовании быстрого алгоритма возведения в степень на выполнение одной итерации зашифрования потребуется не более
, то при использовании быстрого алгоритма возведения в степень на выполнение одной итерации зашифрования потребуется не более 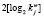 операций умножений. Если учесть, что имеем w < L, то, очевидно, разработанный метод нелинейного шифрования с использованием операции возведения в степень в сумме конечных полей Галуа позволяет повысить скорость закрытия информации.
операций умножений. Если учесть, что имеем w < L, то, очевидно, разработанный метод нелинейного шифрования с использованием операции возведения в степень в сумме конечных полей Галуа позволяет повысить скорость закрытия информации.
Результаты исследования и их обсуждение
Рассмотрим реализацию разработанного метода нелинейного шифрования с использованием операции возведения в степень в сумме конечных полей Галуа. В качестве конечных полей Галуа выбираем GF(23) с порождающим полиномом 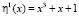 , GF(24) с порождающим полиномом
, GF(24) с порождающим полиномом 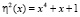 и GF(25) с порождающим полиномом
и GF(25) с порождающим полиномом 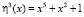 . Пусть задан поток открытых данных, представленный в шестнадцатеричной системе счисления
. Пусть задан поток открытых данных, представленный в шестнадцатеричной системе счисления 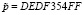 . Для получения ключевой последовательности был использован генератор ПСП, с выхода которого была снята последовательность чисел
. Для получения ключевой последовательности был использован генератор ПСП, с выхода которого была снята последовательность чисел 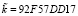 . Так как степень первого порождающего полинома равна
. Так как степень первого порождающего полинома равна 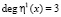 , второго полинома –
, второго полинома – 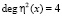 , а третьего многочлена –
, а третьего многочлена – 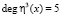 , входной поток разбиваем по блоками по 12 бит. Аналогично поступаем и с ключевой последовательностью.
, входной поток разбиваем по блоками по 12 бит. Аналогично поступаем и с ключевой последовательностью.
Рассмотрим первую итерацию процесса зашифрования. Для этого представим данные в двоичном коде. Тогда получаем
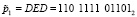 ;
; 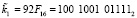 .
.
Таким образом, для поля Галуа GF(23) получаем значения первого блока данных 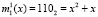 и ключа
и ключа 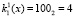 . Для поля Галуа GF(24) значение первого блока данных равно
. Для поля Галуа GF(24) значение первого блока данных равно 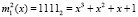 , а значение ключа
, а значение ключа 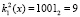 . Для поля Галуа GF(25) получаем первый блок данных равный
. Для поля Галуа GF(25) получаем первый блок данных равный 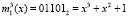 , а значение ключа
, а значение ключа 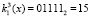 . Воспользуемся выражением (12). Получаем
. Воспользуемся выражением (12). Получаем
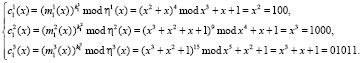
Выполним вторую итерацию шифрования. Тогда получаем
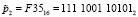 ;
; 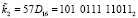 .
.
Таким образом, для поля Галуа GF(23) получаем значения первого блока данных равный 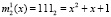 и ключа
и ключа 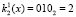 . Для поля Галуа GF(24) значение первого блока данных равно
. Для поля Галуа GF(24) значение первого блока данных равно 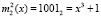 , а значение ключа
, а значение ключа 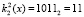 . Для поля Галуа GF(25) получаем первый блок данных равный
. Для поля Галуа GF(25) получаем первый блок данных равный 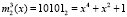 , а значение ключа
, а значение ключа 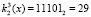 . Тогда получаем
. Тогда получаем
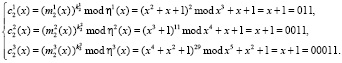
Выполним третью итерацию шифрования. Тогда получаем
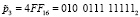 ;
; 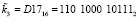 .
.
Для поля Галуа GF(23) получаем значения первого блока данных равные 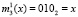 и ключа
и ключа 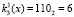 . Для поля Галуа GF(24) значение первого блока данных равно
. Для поля Галуа GF(24) значение первого блока данных равно 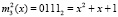 , а значение ключа
, а значение ключа 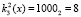 . Для поля Галуа GF(25) получаем первый блок данных равный
. Для поля Галуа GF(25) получаем первый блок данных равный 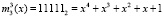 , а значение ключа
, а значение ключа 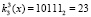 . Тогда получаем
. Тогда получаем
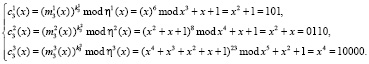
В рассмотренном примере имеем 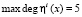 . Тогда при использовании быстрого алгоритма возведения в степень на выполнение одной итерации зашифрования потребуется
. Тогда при использовании быстрого алгоритма возведения в степень на выполнение одной итерации зашифрования потребуется 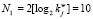 операций умножений. Так как
операций умножений. Так как 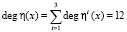 бит, то для выполнения операции возведения в степень по модулю η(х) потребуется
бит, то для выполнения операции возведения в степень по модулю η(х) потребуется 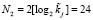 операций умножения. Таким образом очевидно, что разработанный метод нелинейного шифрования с использованием операции возведения в степень в сумме конечных полей Галуа позволяет повысить скорость закрытия информации в 2,4 раза по сравнению с использованием одного модуля разрядностью 12 бит.
операций умножения. Таким образом очевидно, что разработанный метод нелинейного шифрования с использованием операции возведения в степень в сумме конечных полей Галуа позволяет повысить скорость закрытия информации в 2,4 раза по сравнению с использованием одного модуля разрядностью 12 бит.
Выводы
В статье рассмотрен вопрос повышения помехозащищенности низкоорбитальных систем спутниковой связи за счет увеличения информационной скрытности НССС. Для достижения поставленной цели было предложено использовать криптографические методы защиты информации. Проведенные исследования систем шифрования показали целесообразность применения нелинейных методов зашифрования, в которых применяются мультипликативные и аддитивные операции в полях Галуа. В статье приведен разработанный метод нелинейного шифрования данных на основе процедуры возведения в степень для поля Галуа. Проведенные исследования показали, что использование данного метода нелинейного шифрования, реализованного в сумме конечных полей Галуа, позволяет повысить скорость закрытия информации в 2,4 раза по сравнению с использованием одного модуля разрядностью 12 бит.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.



