Возрастающая роль информационных технологий в развитии общества предполагает увеличение числа работников, способных к их эффективному применению, что находит отражение в сфере образования [1, 2]. Большое внимание в образовательных программах по информационным технологиям уделяется практической подготовке. При этом широко используется компьютерное моделирование, позволяющее, в частности, имитировать работу изучаемых объектов [3]. Разработка и развитие технологий использования в учебном процессе компьютерных моделей является актуальной задачей, так как способствует повышению эффективности обучения.
Цель исследования: разработка технологии построения и использования действующих функциональных моделей узлов и блоков ЭВМ при проведения практических занятий в компьютерном классе.
В процессе изучения вопросов организации и функционирования вычислительных машин большое внимание уделяется узлам и блокам, используемым при их построении. При этом во многих случаях можно отвлечься от конструктивного исполнения и особенностей физических процессов, лежащих в основе работы рассматриваемых узлов и блоков, и ограничиться анализом выполняемых ими функций. Ориентация на функциональные структуры позволяет использовать в учебном процессе функциональные модели узлов и блоков. Действующие функциональные модели узлов и блоков могут быть созданы на компьютерах в виде программных моделей [4]. Причем, если обучающиеся знакомы с инструментальными средствами создания программных моделей, то, учитывая относительную простоту рассматриваемых объектов моделирования, они могут самостоятельно разрабатывать и реализовывать функциональные модели узлов и блоков на практических (лабораторных) занятиях. Представляет интерес использование в качестве инструментального средства моделирования популярного табличного процессора Microsoft Excel, обладающего необходимыми возможностями и подтвердившего целесообразность нетрадиционного применения [5].
В предлагаемой технологии построения действующих функциональных моделей узлов и блоков ЭВМ при проведении практических занятий на компьютере с использованием табличного процессора Microsoft Excel выделяются следующие этапы.
1. Анализ задания по разработке функциональной модели. Анализ предполагает содержательное определение функций заданного узла (блока) определение состава всех внешних входов и выходов.
2. Описание работы узла (блока) с помощью формул булевых функций. Предполагается, что моделируемые узлы представляют собой комбинационные схемы (сумматоры, дешифраторы, мультиплексоры и т.п.), а моделируемые блоки включают определенный набор подобных схем. Работа таких узлов и блоков может быть описана системами булевых функций, представленных в виде формул.
3. Разработка схемы. На основе формул булевых функций, описывающих работу узла, строится его функциональная схема. Блок, состоящий из набора узлов, представляется структурной схемой.
4. Разработка экранной формы для экспериментального исследования. Экранная форма создается на листе табличного процессора Microsoft Excel с использованием инструментов вставки фигур и средств рисования. Экранная форма содержит схему исследуемого узла (блока) с полями ввода исходных данных и полями отображения вычисляемых результатов.
5. Построение функциональной модели. Функциональная модель узла (блока) создается на листе табличного процессора Microsoft Excel на основе экранной формы и формул булевых функций, описывающих его работу. Работа узла (блока) моделируется путем реализации формул булевых функций с помощью логических функций табличного процессора Microsoft Excel.
6. Экспериментальные исследования функциональной модели. Экспериментальные исследования заключаются во вводе формул логических функций MS Excel, используемых для моделирования узла (блока), и отладке созданной функциональной модели. В процессе экспериментальных исследований осуществляется проверка правильности работы функциональной модели.
7. Оформление отчета по результатам работы. Отчет может включать: титульный лист, задание на разработку функциональной модели, формулы булевых функций и их представление логическими функциями Microsoft Excel, экранные формы листов Microsoft Excel со схемой узла (блока), таблицу с результатами работы узла (блока).
Рассмотрим выполнение основных этапов технологии построения и использования действующих функциональных моделей узлов и блоков ЭВМ при проведения практических занятий на компьютере на примерах.
Разработка функциональной модели узла
Задание. Разработать функциональную модель узла инкремента. На информационный вход узла поступает 4-разрядный двоичный код X = x3x2x1x0, а на вход переноса p0 – одноразрядный двоичный код. При p0 = 0 на информационный выход Y = y3y2y1y0, поступает код со входа без изменения. При p0 = 1 на информационном выходе формируется увеличенный на единицу 4-разрядный двоичный код. При этом, если на информационном входе во всех разрядах единицы, то на информационном выходе устанавливается нулевой код, а на выход переноса p4 поступает единица.
Описание работы узла с помощью системы булевых функций. Работа 4-разрядного узла инкремента может быть описана следующей системой булевых функций:
yn-1 = xn-1⊕pn-1, pn = xn-1&pn-1, n = 1, 2, 3, 4.
Разработка функциональной схемы узла. На основе системы булевых функций, описывающей работу узла, может быть построена его функциональная схема. Функциональная схема узла инкремента изображена на рис. 1.
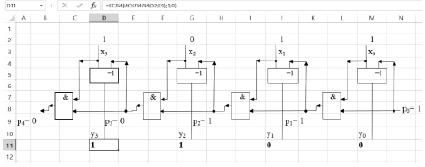
Рис. 1. Функциональная схема узла инкремента
Разработка экранной формы для экспериментального исследования узла. Пример экранной формы, содержащей поля ввода разрядов двоичного кода X = x3x2x1x0 и поле ввода одноразрядного двоичного кода переноса p0 показан на рис. 1. На форме имеются поля для вывода разрядов результирующего двоичного кода Y = y3y2y1y0 и значения переноса из старшего разряда p4. На экран также выводятся значения переносов: p1, p2, p3.
Построение функциональной модели узла. Функциональная модель узла на основе экранной формы и системы булевых функций, описывающих его работу. Работа узла моделируется путем реализации формул булевых функций с помощью логических функций табличного процессора Microsoft Excel (табл. 1).
Таблица 1
Реализация формул булевых функций
|
Формула булевой функции |
Лист Microsoft Excel |
|
|
Адрес ячейки |
Формула |
|
|
y0 = x0⊕p0 |
M11 |
= ЕСЛИ(ИСКЛИЛИ(M2;O8);1;0) |
|
p1 = x0&p0 |
K9 |
= ЕСЛИ(И(M2;O8);1;0) |
|
y1 = x1⊕p1 |
J11 |
= ЕСЛИ(ИСКЛИЛИ(J2;K9);1;0) |
|
p2 = x1&p1 |
H9 |
= ЕСЛИ(И(J2;K9);1;0) |
|
y2 = x2⊕p2 |
G11 |
= ЕСЛИ(ИСКЛИЛИ(G2;H9);1;0) |
|
p3 = x2&p2 |
E9 |
= ЕСЛИ(И(G2;H9);1;0) |
|
y3 = x3⊕p3 |
D11 |
= ЕСЛИ(ИСКЛИЛИ(D2;E9);1;0) |
|
p4 = x3&p3 |
B9 |
= ЕСЛИ(И(D2;E9);1;0) |
Экспериментальные исследования функциональной модели узла. В процессе экспериментальных исследований осуществляется ввод логических функций Microsoft Excel, проверка правильности работы функциональной модели узла, которая в данном случае может быть проведена путем полного перебора сочетаний значений входных переменных и сравнения соответствующих им выходных значений со значениями, полученными экспериментальным путем.
Разработка функциональной модели арифметико-логического блока
Задание 2. Разработать функциональную модель арифметико-логического блока (АЛБ) с двумя 8-разрядными информационными входами и одним 8-разрядным информационным выходом, а также со входом переноса в младший разряд, реализующего четыре микрооперации и два логических условия. АЛБ имеет четыре управляющих входа для выполнения микроопераций и два выхода логических условий. Выполняемые микрооперации: суммирование, исключающее ИЛИ, конъюнкция, логический сдвиг на один разряд в сторону старших разрядов с записью в младший разряд значения со входа переноса. Формируемые логические условия: Z – признак равенства нулю полученного результата, P – перенос из старшего разряда (формируется при суммировании и сдвиге).
Описание работы АЛБ с помощью формул булевых функций. АЛБ имеет два информационных входа, на которые могут поступать исходные данные: на первый вход двоичный 8-разрядный код X = x7x6x5x4x3x2x1x0, а на второй – Y = y7y6y5y4y3y2y1y0, и один информационный выход, где формируется результат: 8-разрядный двоичный код W = w7w6w5w4w3w2w1w0. Кроме того, АЛБ имеет вход переноса p0, на который можно подавать сигнал логического нуля или единицы. Управляющие сигналы и выполняемые микрооперации: v0 – суммирование: A = X + Y + p0, v1 – исключающее ИЛИ: B = X⊕Y, v2 – конъюнкция: C = X&Y, v3 – логический сдвиг на один разряд в сторону старших разрядов с записью в младший разряд значения со входа переноса: D = 2Y.p0. Выполнение микрооперации осуществляется при единичном значении управляющего сигнала, при этом управляющие сигналы других микроопераций равны нулю.
Микрооперации и логические условия можно описать следующими системами булевых функций. Суммирование: an-1 = v0&(xn-1⊕yn-1⊕pn-1), pn = v0&(xn-1&yn-1∨ xn-1&pn-1∨yn-1&pn-1), n = 1,…,8. p0 = 1 (p0 = 0). Исключающее ИЛИ: bn-1 = v1&(xn-1⊕yn-1), n = 1,…,8. Конъюнкция: cn-1 = v2&(xn-1&yn-1), n = 1,…,8. Логический сдвиг в сторону старших разрядов: q = y7, dn = v3&yn-1, n = 1,…,7, d0 = v3&p0. Результат, формируемый на выходе АЛБ: wn-1 = an-1∨bn-1∨cn-1∨dn-1, n = 1,…,8. Признак равенства нулю результата: 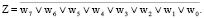 Признак переноса из старшего разряда: P = v0&p8∨v3&q.
Признак переноса из старшего разряда: P = v0&p8∨v3&q.
Разработка схемы блока. На основе системы булевых функций АЛБ может быть построена схема, описывающая его функционирование (рис. 2). АЛБ содержит четыре основные логические схемы микроопераций: SM (суммирования); LS1 (исключающего ИЛИ); LS2 (конъюнкции); LS3 (логического сдвига в сторону старших разрядов), а также вспомогательную логическую схему LS4, которая позволяет выдавать результат выполняемой микрооперации на выход W АЛБ. На логические схемы микроопераций (SM, LS1, LS2, LS3) кроме исходных данных поступает соответствующий управляющий сигнал (v0,v1,v2,v3), а на сумматор и сдвигатель – еще и сигнал переноса в младший разряд (p0). Выдачу на выход P одного из сигналов переполнения: при суммировании (p8) или сдвиге (q) чисел обеспечивает двухвходовой логический элемент ИЛИ. На выходе Z с помощью 8-входового логического элемента ИЛИ – НЕ формируется сигнал равенства нулю результата любой микрооперации.
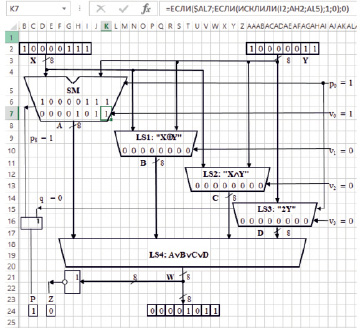
Рис. 2. Схема арифметико-логического блока
Разработка экранной формы для экспериментального исследования АЛБ. Пример экранной формы для исследования АЛБ показан на рис. 2. В верхней части экранной формы расположены два 8-разрядных поля ввода исходных данных X и Y. В правой части экранной формы расположены одноразрядные поля для ввода управляющих сигналов (v0,v1,v2,v3) и сигнала переноса в младший разряд (p0). Микрооперации представлены на экранной форме логическими схемами (SM, LS1, LS2, LS3), на которых отображаются 8-разрядные поля вычисляемых результатов. На сумматоре (внизу) кроме вычисленной суммы дополнительно отображается 8-разрядное слово переносов. В нижней части экранной формы показан информационный выход, где формируется результат: 8-разрядный двоичный код W. В левой части экранной формы отображаются признаки переноса из старшего разряда при суммировании (p8) и сдвиге (q), а также общие признаки переноса из старшего разряда (P) и равенства нулю результата (Z).
Построение функциональной модели блока. Работа АЛБ моделируется путем реализации формул булевых функций с помощью логических функций табличного процессора Microsoft Excel. Реализация формул булевых функций показана в табл. 2, где ввиду однотипности формул, соответствующих отдельным разрядам (исключение составляют формулы для младших разрядов результата в микрооперациях суммирования и сдвига) в таблице для всех микроопераций приводятся формулы для младшего разряда, а для микроопераций суммирования и сдвига – еще и для старшего разряда результата.
Таблица 2
Реализация формул булевых функций
|
Микрооперация / Формула булевой функции |
Лист Microsoft Excel |
|
|
Адрес ячейки |
Формула |
|
|
Суммирование |
||
|
a0 = v0&(x0⊕y0⊕p0), p0 = 1 (p0 = 0) |
K7 AL5 |
= ЕСЛИ($AL7;ЕСЛИ(ИСКЛИЛИ(I2;AH2;AL5);1;0);0) 1 или 0 |
|
a7 = v0&(x7⊕y7⊕p7), p7 = v0&(x6&y6∨x6&p6∨y6&p6) |
D7 E6 |
= ЕСЛИ($AL7;ЕСЛИ(ИСКЛИЛИ(B2;AA2;E6);1;0);0) = ЕСЛИ($AL7;ЕСЛИ(ИЛИ(И(C2;AB2);И(C2;F6);И(AB2; F6));1;0);" ") |
|
p8 = v0&(x7&y7∨x7&p7∨y7&p7) |
E9 |
= ЕСЛИ($AL7;ЕСЛИ(ИЛИ(И(B2;AA2);И(B2;E6);И(AA2; E6));1;0);0) |
|
Исключающее ИЛИ |
||
|
b0 = v1&(x0⊕y0) |
T10 |
= ЕСЛИ($AL10;ЕСЛИ(ИСКЛИЛИ(I2;AH2);1;0);0) |
|
Конъюнкция |
||
|
b0 = v1&(x0&y0) |
AB13 |
= ЕСЛИ($AL13;ЕСЛИ(И(I2;AH2);1;0);0) |
|
Логический сдвиг |
||
|
d0 = v3&p0, d7 = v3&y6, q = y7 |
AC16 Z16 F14 |
= ЕСЛИ($AL16;AL5;0) = ЕСЛИ($AL16;AB2;0) = ЕСЛИ($AL16;AA2;0) |
|
Результат |
||
|
w0 = a0∨b0∨c0∨d0 |
W21 |
= ЕСЛИ(ИЛИ(K7;T10;AB13;AG16);1;0) |
|
Признак Z |
E21 |
= ЕСЛИ(НЕ(ИЛИ(P21:W21));1;0) |
|
Признак P |
C21 |
= ЕСЛИ(ИЛИ(И(AL7;E9);И(AL16;F14));1;0) |
Экспериментальные исследования функциональной модели АЛБ. В процессе экспериментальных исследований осуществляется проверка правильности выполнения микроопераций и формирования логических условий. В табл. 3 приведены примеры выполнения микроопераций и формирования логических условий.
Таблица 3
Результаты вычисления микроопераций и логических условий
|
№ |
v0 |
v1 |
v2 |
v3 |
МО |
X |
Y |
p0 |
W |
Z |
P |
|
1 |
1 |
0 |
0 |
0 |
Суммирование |
10001001 |
10000101 |
1 |
00001111 |
0 |
1 |
|
2 |
0 |
1 |
0 |
0 |
Исключающее ИЛИ |
10001001 |
10000101 |
1 |
00001100 |
0 |
0 |
|
3 |
0 |
0 |
1 |
0 |
Конъюнкция |
10000111 |
10000001 |
1 |
10000001 |
0 |
0 |
|
4 |
0 |
0 |
0 |
1 |
Сдвиг |
10000001 |
1 |
00000011 |
0 |
1 |
|
|
5 |
0 |
1 |
0 |
0 |
Исключающее ИЛИ |
00001100 |
00000011 |
1 |
00001111 |
0 |
0 |
|
6 |
0 |
0 |
1 |
0 |
Конъюнкция |
00001100 |
10000011 |
1 |
00000000 |
1 |
0 |
В таблице суммирование исходных чисел X = 10001001 и Y = 00001111 произведено двумя способами: с помощью сумматора (строка 1) и с использованием специального циклического алгоритма (строки 2–6). Во втором случае суммирование требует нескольких шагов. На каждом шаге выполняются следующие действия: вычисляется сумма по модулю два (исключающее ИЛИ) и конъюнкция исходных данных, если конъюнкция равна нулю, то полученная сумма по модулю два является результатом суммирования, иначе производится логический сдвиг конъюнкции на один разряд в сторону старших разрядов и она, и сумма по модулю два выступают в качестве исходных данных для следующего шага. В табл. 3 вычисления завершаются на втором шаге (строка 6). Оба способа вычисления суммы чисел дают одинаковый результат (строки 1 и 5).
Технология построения и исследования узлов и блоков ЭВМ имеет следующие достоинства: обучающиеся самостоятельно разрабатывают функциональные модели изучаемых объектов; используется широко распространенное в образовательных организациях программное обеспечение, приобретать специальные программы не требуется; применяемая программа предоставляет необходимые средства для ввода и редактирования данных, построения схем моделируемых узлов и блоков; обучающиеся и преподаватели, как правило, знакомы с программой, которая используется в компьютерном практикуме; большое число функций, выполняемых узлами и блоками ЭВМ, при необходимости позволяет сформировать различные варианты индивидуальных заданий для построения функциональных моделей; практикум открыт для последующего развития и адаптации в зависимости от особенностей учебного процесса и предпочтений преподавателя.
Заключение
Предлагаемый подход к организации практических занятий способствует формированию компетенций, связанных с функционально-структурным анализом и синтезом узлов и блоков вычислительных машин, и полезен при преподавании основ информатики и вычислительной техники. Технология построения и исследования узлов и блоков ЭВМ разрабатывалась для студентов младших курсов, обучающихся по основным профессиональным образовательным программам бакалавриата. После соответствующей адаптации технология может быть применена в образовательных организациях, реализующих образовательные программы общего среднего и среднего профессионального образования.



