Сельскохозяйственная мелиорация – это изменение природной среды с целью ее улучшения для ведения сельского хозяйства (Н.Ф. Реймерс, 1990). Объектами мелиорации являются неблагоприятные гидрологические, почвенные и климатические условия. Организационно-хозяйственные мероприятия при осуществлении мелиоративных работ предполагают внедрение высоких технологий [1, 2]. При этом необходимо учитывать следующие критерии экологической оценки состояния почв – не допускать увеличения плотности почвы, превышения уровня грунтовых вод, превышения предельно допустимой концентрации загрязняющего вещества.
При составлении мелиоративного проекта необходимо провести анализ подходов к улучшению состояния мелиорируемых земель и на этой основе осуществить эколого-экономическую оценку их применения.
В последние годы явления деградации почв углубились из-за резкого подорожания минеральных удобрений, из-за недостатка средств на мелиоративные мероприятия. В этой связи требуется обоснование приемов регулирования процессов на мелиорируемых землях, поиск новых приемов, дешевле существующих, менее трудоемких при их выполнении и отвечающих экологическим требованиям. Возникает необходимость рассмотрения различных вариантов проекта, введения новых показателей эффективности природоохранных проектов.
В каждом мелиоративном проекте проводится анализ влияния намечаемых мероприятий на окружающую среду. Особенность оценки эффективности природоохранных проектов состоит в необходимости учета вероятностного характера происходящих процессов [3, 4]. Для учета стохастического характера процессов необходим выбор подходящих вероятностных моделей. В Кубанском государственном аграрном университете в программе магистратуры цель курса «Математическое моделирование процессов в компонентах природы» – научить обучающихся использовать современные подходы науки в методике исследований водохозяйственного комплекса природообустройства.
Материалы и методы исследования
Большинство данных, используемых в мелиоративных исследованиях, являются стохастическими величинами. Это обстоятельство не позволяет находить однозначные решения. Возникает необходимость выполнить оценку пределов допустимых колебаний переменных величин. Такие оценки эффективнее выполнять на моделях с использованием математической статистики. Приведем примеры.
Первый пример. Так как состояние почв обусловлено большим количеством случайных факторов, необходим вероятностный подход к выбору управленческих решений [3–5]. При таком подходе параметры, характеризующие мелиоративную систему, трактуются случайными величинами. Это позволяет рассматривать неопределенность, связанную с оценкой параметров, в терминах вероятностных распределений.
Второй пример. Для совершенствования технологии орошения с применением фертигации необходима разработка математической модели процессов влаго- и солепереноса. Фертигация – орошение с использованием растворимых удобрений и систем капельного полива. Совместное нормированное внесение в почву воды и удобрений является технологической и экологической основой оптимизации условий выращивания высоких урожаев сельскохозяйственных культур. Этот прием позволяет постоянно поддерживать влажность воздуха и почвы в оптимальной пропорции в системе «вода – воздух» в почве, подавать растениям удобрения небольшими дозами, способствует повышенной усвояемости удобрений, меньшей выщелачиваемости в сравнении с традиционными методами ирригации.
Моделирование процесса управления водно-солевым режимом во фрактальных средах рассмотрено в работах [6, 7]. Французский математик Б. Мандельброт определяет фракталы раздробленными объектами, которые выглядят одинаковыми в любом масштабе [8]. В работах [6, 7] авторы рассматривают почву сложной пористой фрактальной структурой. Целью фрактального анализа является исследование фрактальных свойств, оценка их глубины и значение показателя Н. Херста. В теории используют термин R/S-анализ, который называется «методом нормированного размаха Херста».
При использовании метода нормированного размаха рассматривается ряд n последовательных величин x1, x2,…xn. Каждое xi,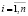 
характеризует временное положение исследуемой величины. Влажность почвы определяет фрактальные качества почвенных коллоидов, а фрактальная размерность – изменение масштаба, степень изменчивости ряда. По выборке x1, x2,…xn рассчитываются выборочные статистические характеристики: среднее арифметическое, дисперсия, стандарт, коэффициент вариации. Они являются оценками соответствующих генеральных статистических параметров [8].
Результаты исследования и их обсуждение
Рассмотрим математическую модель первого примера.
Пусть в момент начала работ намечены мелиоративные мероприятия на длительность функционирования Т1, цена которых S1. Si – затраты, связанные с регулированием или полным устранением отрицательных последствий мелиоративных мероприятий.
Если за время Т1 отрицательные последствия мелиоративных мероприятий не устранены, намечаются новые мелиоративные мероприятия, цена которых S2 и длительность функционирования Т2.
Если за время Т2 отрицательные последствия не устранены, намечаются новые мелиоративные мероприятия на длительность функционирования Т3 и цене S3 и т.д. Каждый отрезок времени будем называть фазой. Длительность фазы поставим в зависимость от числа намечаемых мероприятий.
Пусть в начальный момент устанавливается цена S1. Мелиоративные мероприятия вводятся в эксплуатацию, m1 – число возможных мероприятий. Если удовлетворительное состояние будет достигнуто – процесс закончен. Если выбранные m1 мероприятий не приводят к удовлетворительному состоянию, то намечаются m2 возможных мероприятия, цена которых S2. Если намеченные мероприятия приводят систему к приемлемому состоянию – процесс закончен, если нет – выбираются другие m3 возможных мероприятия, оцениваемых ценой S3, и т.д. Этот процесс пояснен рисунком.
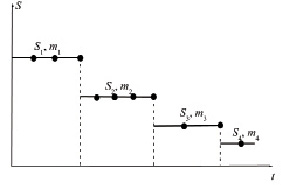
Модель выбора намечаемых мероприятий с понижением цены
Можно рассматривать последовательность мелиоративных мероприятий пуассоновским потоком интенсивности l. На п-й фазе удовлетворительное мелиоративное состояние будет достигнуто с вероятностью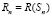 
.
Рассмотрим i-ю фазу. Тогда с вероятностью
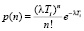(1)
на ней будет выполнено п выбранных мероприятий. Так как Ri есть вероятность достижения удовлетворительного мелиоративного состояния при конкретном мероприятии, то с вероятностью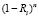 
удовлетворительное состояние не будет достигнуто. Пусть Pi – вероятность того, что на i-й фазе удовлетворительное состояние не достигнуто.
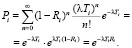(2)
Обозначим Qn – вероятность того, что удовлетворительное состояние достигнуто на п-й фазе. На предыдущих фазах с номерами 1, 2, 3, … , n – 1 мелиоративное состояние неудовлетворительно. Потому
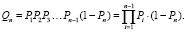(3)
Используя выражение (2), получим
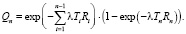
Теперь можем рассмотреть основные характеристики цены удовлетворительного мелиоративного состояния.
Выполненное мероприятие доводит систему до определенного состояния с вероятностью R(S), зависящей от цены S(t). R(S) – монотонно убывающая функция, так что с уменьшением цены мероприятий вероятность достижения ущерба возрастает.
Если удовлетворительное мелиоративное состояние будет достигнуто на n-м отрезке времени (п-й фазе), то цена выполненных мероприятий будет равна Sn. Потому отмечаем, цена Se – дискретная случайная величина, принимающая значения Sn с вероятностями Qn
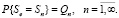(4)
Следовательно,
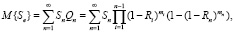(5)
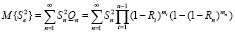
и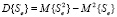 
.
Полученные характеристики случайной величины (цены намечаемых мелиоративных мероприятий с учетом неопределенностей) могут быть использованы в управленческих решениях [9].
Для оценки статистических параметров дискретной случайной величины второго примера можно использовать известные формулы математической статистики [10].
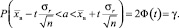(6)
Формулой (6) определен искомый доверительный интервал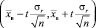 
для неизвестного параметра M(X) = a c заданной заранее доверительной вероятностью γ при n > 30 (n – объем выборки). Концы этого интервала содержат две неизвестные величины t и σr. Первая из них находится из соотношения 2Φ(t) = γ, откуда 
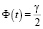и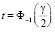 
, где Φ-1(x) есть функция, обратная функции Лапласа.
Тогда (6) приобретает вид
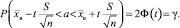(7)
Пример. По данным выборки из генеральной совокупности, приведенным ниже в таблице, найти с вероятностью γ = 0,95 доверительный интервал для неизвестного X – органических добавок в почву.
Выборка из генеральной совокупности
|
X = xi |
100 |
300 |
500 |
700 |
900 |
|
n |
5 |
20 |
40 |
25 |
10 |
Решение.
Выборка большая (n > 30)
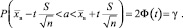
1. Найдем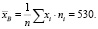 
2. Найдем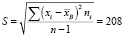 
.
3. Найдем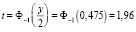 
.
4. Найдем характеристику точности оценки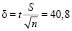 
.
5. Найдем доверительные границы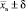 
, что даст
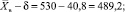
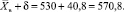
Cледовательно, с 95 %-ной уверенностью (надежностью) неизвестный параметр M(X) = a принадлежит интервалу (489,2; 570,8), т.е. 489,2 < a < 570,8, или, иначе, a = 530 ± 40,8 с вероятностью γ = 0,95.
Смысл полученного результата: если произвести достаточно большое число различных выборок из генеральной совокупности с объемами n = 100 единиц, то в 95 % из них неизвестное M(X) = a будет находиться в полученном интервале (489,2; 570,8) и лишь в остальных 5 % M(X) может оказаться за пределами этого интервала [10].
Примечание. Из формулы для точности оценки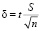 
следует, что, чем больше объем выборки n, тем точность оценки лучше, так как 
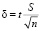убывает с ростом n.
Наоборот, если потребовать увеличение надежности оценки (например, γ = 0,99 или γ = 0,999), то увеличится значение функции Лапласа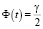 
, а вместе с ней и значение аргумента, ибо Φ(t) – возрастающая функция t. Но тогда увеличится и δ, и точность оценки δ ухудшится.
Иначе говоря, худшая точность более вероятна, чем лучшая, что вполне естественно.
Выводы
Приемы мелиорации обеспечивают повышение плодородия почв. С изменением экологических условий и развитием технического прогресса приемы улучшения условий жизни сельскохозяйственных культур постоянно совершенствуются, разрабатываются новые технические средства регулирования режимов почв. Необходимо количественно оценивать мероприятия, их состав, объем, очередность, сроки ввода. Рассмотренные вопросы нахождения числовых характеристик случайных величин и доверительных интервалов для средних величин магистранты используют при оформлении курсовых работ по дисциплине «Математическое моделирование природных процессов в компонентах природы».