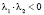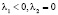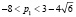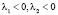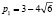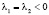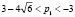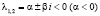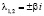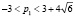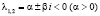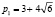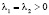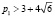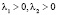В последние годы в кругах педагогической общественности высшей школы много говорится о возросшей роли самостоятельной работы студентов и ее значении для формирования компетенций будущего специалиста. Одной из форм самостоятельной работы являются лабораторные работы. На наш взгляд, количество лабораторных работ в целом в высшей школе надо увеличивать. Особенно их постановка важна в наукоемких дисциплинах: физике, математике, информатике и др. Проведение лабораторных работ по курсу теории систем также актуально и целесообразно, ибо здесь присутствует комплексность формируемых знаний и можно четко выделить этапы: 1) физического и математического моделирования; 2) выбора метода исследования; 3) исследования математической модели аналитическим методами; 4) численного решения задачи с использованием ПК и визуализации результатов; 5) анализа полученных результатов.
На кафедре информационных систем и вычислительной техники Санкт-Петербургского горного университета с 2003 г. читается курс математических основ теории систем (кратко «МОТС»). Видное место в нём занимает анализ нелинейных автономных и неавтономных динамических систем второго порядка в фазовом пространстве, описываемых дифференциальными уравнениями как аналитическими, так и численными методами. В нем студенты знакомятся со способами описания динамических систем, их классификацией, с элементами качественной (геометрической) теории дифференциальных уравнений на плоскости и пространстве, с основными понятиями и теоремами теории устойчивости, с дискретными отображениями и различными приложениями этой теории. В курсе много конкретных примеров из механики, электротехники и электроники, гидродинамики, химии, математической теории популяции [1]. Важное место в нем занимают вопросы связи возможных структур фазовых картин динамических систем от параметров. Ответы на эти вопросы содержатся в теории бифуркаций, основателем которой является А. Пуанкаре. Теория бифуркаций, отражающая закон перехода количества в качество, является важной составляющей активно развивающейся сегодня нелинейной динамики – теоретического фундамента целого ряда научных и технических дисциплин. В курсе изучаются элементарные бифуркации в динамических системах на прямой и плоскости. Демонстрируются примеры. Курс предусматривает выполнение студентами ряда лабораторных работ [1], целью проведения которых является закрепление основных положений теории через визуализацию геометрических образов и выработка у студентов определенных навыков исследовательской работы с освоением приемов качественно-численного исследования динамических систем. Выполнение каждого задания в лабораторных работах подразумевает выполнение студентом некоторой теоретической части, включающей этапы, изложенные на лекциях, и вычислительной, включающей проведение ряда целенаправленных вычислительных экспериментов с использованием какой-либо из известных компьютерных систем. В качестве вычислительного инструмента с 2010 г. студенты используют програм- мный комплекс WinSet [2], который в настоящее время приобрел достаточную известность и апробирован во многих вузах страны. Для целей нашего курса WinSet обладает рядом преимуществ в сравнении с программными пакетами MATLAB, MAPLE, Scilab и др., так как имеет удобный интерфейс, прост в использовании и, что немаловажно, – не требует большого времени на изучение. Заметим, что введение в учебный процесс компьютерных методов исследования математических моделей является велением времени и должно стимулировать интерес студентов к изучению аналитических методов, к каковым относятся методы качественной теории дифференциальных уравнений и теории бифуркаций. Результатом проведения обсуждаемых в настоящей статье лабораторных работ должно стать формирование у студента преобразовательной, инновационной и творческой активности. Далее мы приводим несколько типовых лабораторных работ. При желании спектр рассматриваемых в них математических моделей можно расширить в соответствии с будущей специальностью студента.
Лабораторные работы
Первая лабораторная работа по существу является ознакомительной. Во вступительной части преподаватель демонстрирует возможности программы WinSet, приёмы работы с ней и визуализирует некоторые наиболее важные положения теории, изложенной на лекциях [1]. Затем студенты знакомятся с программой самостоятельно на примере качественно-численного исследования линейной системы дифференциальных уравнений вида
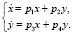
В каждом варианте индивидуальных заданий фиксируются три из четырёх параметров p1, p2, p3, p4. Требуется: 1) провести теоретический анализ системы по оставшемуся параметру с классификацией всех возможных типов состояний равновесия, включая вырожденные случаи; 2) используя программу WinSet, построить соответствующие фазовые картины. Так, для системы [3]
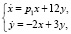
в результате анализа корней характеристического уравнения
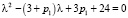
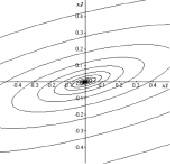
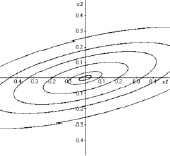
студент должен построить следующую таблицу (таблица), а затем приложить 9 фазовых картин. На рис. 1 мы приводим для примера четыре из них, соответствующие номерам 1, 5, 6, 9 таблицы.
|
№ |
p1 |
Характеристические корни |
Тип положения равновесия |
|
1 |
p1 < –8 |
|
Седло |
|
2 |
p1 = –8 |
|
Вырожденный случай |
|
3 |
|
|
Устойчивый узел |
|
4 |
|
|
Вырожденный устойчивый узел |
|
5 |
|
|
Устойчивый фокус |
|
6 |
p1 = –3 |
|
Центр |
|
7 |
|
|
Неустойчивый фокус |
|
8 |
|
|
Вырожденный неустойчивый фокус |
|
9 |
|
|
Неустойчивый узел |
а) б)
в) г)
Рис. 1. Фазовые портреты линейных систем: a) седло; б) устойчивый фокус; в) центр; г) неустойчивый узел
В следующей лабораторной работе исследуются эталонные динамические системы, играющие в теории колебаний большую феноменологическую роль
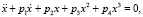
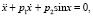
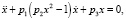
(это уравнения Дуффинга, математического маятника и автогенератора Ван дер Поля). Здесь студенты определяют состояния равновесия, проводят линеаризацию уравнений в них, устанавливают типы состояний равновесия, в случае p1 = 0 находят первые интегралы уравнений и строят инвариантные кривые. Далее проводят анализ векторного поля систем по параметру p1. На втором этапе, используя программу Winset, студенты строят фазовые портреты консервативных (p1 = 0) и диссипативных (p1 > 0) систем, моделируют сепаратрисы седловых состояний равновесия и анализируют зависимость формы предельных циклов в уравнении Ван дер Поля от параметров (рис. 2, 3).
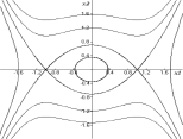
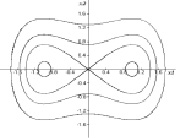
а) б)
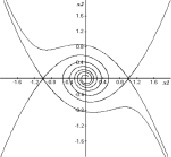
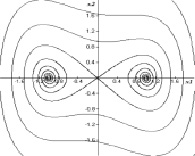
в) г)
Рис. 2. Типовые фазовые картины: a), б) консервативные системы; в), г) диссипативные системы
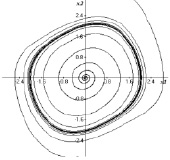
Рис. 3. Предельный цикл уравнения автогенератора Ван дер Поля
Третья лабораторная работа относится к исследованию бифуркаций в нелинейной системе с параметром p1
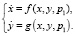
Функции f(x, y, p1), g(x, y, p1) задаются индивидуально в каждом варианте.
Рассмотрим конкретный пример такого задания [4].
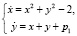
и кратко сформулируем результаты качественно-численного исследования, которые должен получить студент:
1. При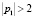 
положений равновесия в системе нет.
2. При p1 = 2 и p1 = –2 возникает бифуркация седло-узла.
3. При p1 = 1,743 происходит бифуркация петли сепаратрисы седла (бифуркация гомоклинической траектории).
4. При переходе через критическое значение p1 = 1,743 из петли сепаратрисы рождается устойчивый предельный цикл.
5. При p1 = 1,8228 возникает обратная бифуркация Андронова – Хопфа (устойчивый цикл «влипает» в неустойчивое положение равновесия и передаёт ему свою устойчивость). Важно, что область p1∈(1,743, 1,8228) отвечает существованию устойчивого предельного цикла. На рис. 4 для p1 = 1,78 приведена фазовая картина (в положении равновесия С1 – седло, в С2 – неустойчивый фокус). Другие фазовые картины мы здесь не приводим.
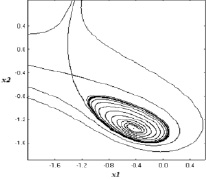
Рис. 4. Седло и устойчивый цикл при p1 = 1,78
Выполнение работы, возможно, потребует от студента самостоятельного изучений ряда дополнительных теоретических вопросов, связанных с теорией бифуркаций [5–7]. На этом этапе определенную помощь должен оказать преподаватель.
Следующая лабораторная работа является наиболее емкой в вычислительном плане. Она знакомит студента со сложным динамическим поведением в простых нелинейных системах. Работа требует большой работы за компьютером и для ее полного выполнения будет нужна внеаудиторная работа (работа дома). Отчетом должна стать карта динамических режимов конкретного нелинейного осциллятора с внешним воздействием. Примерным вариантом такой работы может служить система [1]:
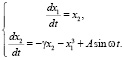
В ней фиксируются два параметра γ и ω и требуется исследовать динамику системы в заданном интервале изменения третьего параметра A∈[α, β]. При выполнении такой работы вполне допустимым будет консультирование студента по электронной почте, так как вопросов может быть много. Отметим, что эта работа знакомит студента с постановкой современных и сложных задач. Экспериментальное решение подобных задач сводится, по существу, к длительному вычислительному эксперименту и может затянуться на многие часы, а студент «незаметно для себя» окажется втянутым в научное исследование. Заметим, что теоретическое исследование этой системы представляет собой трудную математическую задачу не только для студента, но и для состоявшегося математика.
Заключение
Предлагаемые в статье темы лабораторных работ носят в значительной степени междисциплинарный учебный характер и могут проводиться не только по дисциплине МОТС. Много полезного в них найдут преподаватели кафедр математики, физики, информатики, радиотехники и электроники, а также других дисциплин. Рассмотренные в лабораторных работах математические модели непринципиальны. Много интересных примеров сегодня дает химия, биология, экономика. Работы носят комплексный характер и включают элементы качественной теории и теории бифуркаций (на наш взгляд, сегодня они слабо отражены в учебных программах технических вузов), теории нелинейных колебаний, а также компьютерную технологию работы с новым программным продуктом. Такой подход оправдан целью формирования профессиональной компетентности специалиста широкого инженерного профиля и креативности его мышления. Преподавателям высшей технической школы хорошо знакома проблема разрыва между уровнем преподавания дифференциальных уравнений и уровнем современной математической науки. К сожалению, в ряде втузов страны теория дифференциальных уравнений, являющаяся фундаментом многих научных и технических дисциплин, излагается в объеме, включающем классические результаты, полученные еще к середине XIX в., а примеры, рассматриваемые в них, носят модельный – оторванный от приложений характер. Темы обсуждаемых лабораторных работ конкретны (физическую сущность приведенных моделей мы здесь не обсуждали) и должны послужить активизации познавательной деятельности студента, пробудить в нем интерес не только к абстрактной теории систем, но и к ее огромным приложениям в науке и технике, а также в целом повысить мотивацию обучаемых к научно-исследовательской работе. Эти знания студентам явно пригодятся. С методической точки зрения работы построены по естественному принципу и ведут студента от понимания простых вещей к пониманию сложных и важных [10], вселяя в него постепенно уверенность в своих силах. Сегодня абсолютно ясно, что необходимо учить не рецептам решения задач, не пустому заучиванию алгоритмов и схем, а исследованию. Хорошо известен тезис, что нельзя научиться думать, если не думать самому. Действовать по шаблону, конечно, проще, но, к сожалению, это скучно. Потеря же интереса к предмету у обучаемого говорит о двух вещах: либо он не туда попал, но мы это не обсуждаем, либо об ошибке преподавателя – не смог заинтересовать предметом. Ставя эти работы, мы реализовали системно-деятельный подход и преследовали цель пробудить интерес к фундаментальным знаниям через вычислительный эксперимент, компьютерное моделирование, так как наглядные образы всегда являлись стимулами к познанию нового (полезно напомнить, что там, где в науке можно что-то нарисовать – надо рисовать). При проведении лабораторных работ, как хорошо известно, активность преподавателя уступает место активности студента. Задача педагога заключается в создании благоприятных условий для инициативы студента и «легком адаптивном управлении». При этом студент становится центральной фигурой учебного процесса, а педагог переходит в ранг консультанта и товарища. Сказанное является в настоящее время азбучной истинной, но напомнить ее все-таки следует.