Основа электрокардиографии – регистрация биоэлектрических потенциалов на поверхности кожи организма, возникающих во время работы сердца. Обычно для этого используется стандартный электрокардиограф с двенадцатью отведениями, который улавливает с поверхности тела разницу электрических потенциалов, возникающих в разных отделах сердца в моменты его сокращения и расслабления. В новейших современных электрокардиографах эта информация записывается и подвергается дальнейшей обработке в цифровом виде.
Современный этап развития информационных технологий характеризуется массовым применением систем, использующих различные алгоритмы обработки, анализа и интерпретации сигналов [1, 2], в частности электрокардиограммы (ЭКГ). Классический подход в электрокардиологии состоит в использовании различных методик анализа временных зависимостей амплитуды кардиосигнала: стандартное ЭКГ-измерение – измерение частоты сердечных сокращений, дисперсия реполяризации и т.д. Однако существующие методы анализа во временной и спектральной области не всегда достаточны для описания всех особенностей ЭКГ-сигналов и не позволяют в полной мере выявить его характерные черты [3].
Ключевыми задачами анализа кардио- сигналов является не только обнаружение комплексов и анализ их формы, но и выявления характерных зависимостей в спектре. В этой связи новые возможности открывает использование стандартного преобразования Фурье и спектрального анализа для получения частотно-временного представления сигнала. В основе преобразования Фурье (ПФ) лежит идея представления периодической функции, все сигналы ЭКГ являются именно такими, в виде суммы отдельных гармонических составляющих (синусов и косинусов с различными амплитудами A, периодами Т и, следовательно, частотами ω) [4–6].
Цель работы: определение гармонических составляющих и частотных характеристик ЭКГ-системы посредством спектрального анализа.
Материалы и методы исследования
Для обработки и дальнейшего анализа был взят оцифрованный сигнал первого отведения стандартной электрокардиографической системы, содержащий помехи и наводки. Исходный кардиосигнал представлен на рис. 1 сплошной синей линией.
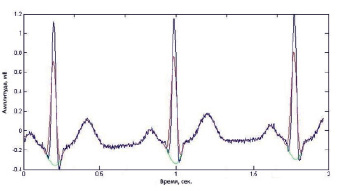
Рис. 1. Отрезок кардиосигнала. Исходный сигнал ЭКГ – синяя линия, сигнал после фильтрации – красная линия, сглаженный сигнал P-QRS-T – зелёная линия
Исходные данные временного ряда первого отведения содержат шумы и наводку, что естественным образом отражается на результатах спектрального анализа в виде высокочастотных помех. Это мешает дальнейшей обработке и определению зависимостей между гармоническими составляющими, частотами и зубцами кардиограммы. Для минимизации шумовой компоненты была реализована первичная обработка во временной области – сглаживание при помощи полиномов Лагранжа-Сильвестра (рис. 1 – красная линия):
Первичная фильтрация в частотной области негативно сказывается на дальнейших результатах обработки. После первичной обработки сигнала во временной области производится спектральный анализ с использованием быстрого преобразования Фурье:
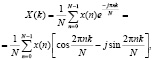
где 0 ≤ k ≤ N – 1, N – количество перемножения комплексных чисел [7, 8].
Для выявления гармонических составляющих и частотных характеристик. Результаты спектрального анализа представлены на рис. 2.
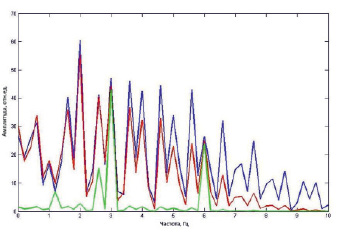
Рис. 2. Спектры ЭКГ-сигнала. Спектр исходного сигнала – синяя линия; спектр отфильтрованного сигнала – красная линия, спектр сигнала после сглаживания – зелёная линия
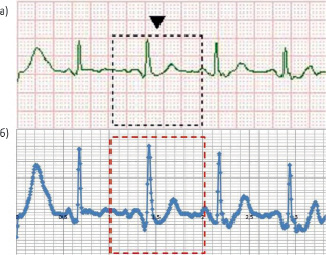
Рис. 3. Представление кардиограммы в аналоговой (а) и дискретной (б) форме
Заметим, что даже после фильтрации полученный спектр сигнала состоит из более чем пятнадцати гармоник. Определение функциональных зависимостей между зубцами кардиограммы и частотами при таком количестве пиков сильно затруднено. Преобразование Фурье предполагает наличие периодического, но сглаженного сигнала. На общепринятых аналоговых ЭКГ сигналах, записанных на миллиметровку, пик R аппроксимируется треугольником, так как он е несколько растянут.
Исходные оцифрованные данные показывают, что тот пик, отвечающий за резкое сжатие желудочков, наиболее близко соответствует δ-функции с амплитудой в 3–5 раз больше чем у пиков P (сжатие предсердий) и T (расслабления желудочков). Это представляет наибольшую «нагрузку» на результаты спектрального анализа. Временное представление ЭКГ сигнала в виде двух функций, периодически появляющегося пика δ-функции и сглаженного сигнала с пиками P и T, приводит к получению спектров с адекватно интерпретируемыми гармоническими составляющими [9, 10]. Интерполирование полученного разрыва при помощи полинома Лагранжа – Сильвестра:
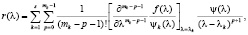
где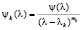 
, удовлетворяющий условиям:
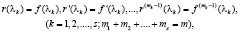
f(λ) – функция, которая определена на спектре матрицы А;
λ(k) – нули минимального полинома ψ(λ) матрицы А;
mk – степень полинома;
практически, дали наилучшие результаты спектрального анализа [10]. Сигнал со сглаженной δ-функцией и интерполированный полиномом Лагранжа представлен на рис. 1 зелёным цветом. Результаты спектрального анализа обработанного сигнала представлены на рис. 2 соответственно.
В спектре полученного сигнала присутствуют две ярко выраженные гармоники с частотами: w1 = 3,12 Гц и w2 = 6,21 Гц. При вычислении частот по стандартной формуле, T = 2π/ω, можно обнаружить, что на кардиограмме w1 соответствует зубцу Р, а w2 зубцу Т. Также отношение амплитуд зубцов P и T на исходном сигнале и результатах спектрального анализа равны, что может говорить об адекватности полученных результатов, соответствующие зубцам P и T. Важно отметить, что гармоники спектра обработанного сигнала примерно кратны 2. Подобное отношение было получено ранее и для немышечной подвижности у простейших организмов [11].
Результаты исследования и их обсуждение
С помощью цифрового полосового фильтра были вырезаны частоты, соответствующие 0,3–3 Гц. Результатом его применения стало исчезновение зубца R. Однако зубцы Q и S не только остались, но и не изменили своей формы. Данный результат вполне объясним. Так как зубец R характеризуется большой амплитудой за малый промежуток времени, что можно интерпретировать как результат наложения синусоид малой частоты и большой амплитуды (рис. 2).
Можно предположить, что полученные частоты от 3,1 до 6,2 Гц соответствуют зубцам Q и S, которые характеризуются малыми характерными временами, что и соответствует данным частотам в спектральном представлении.
Важно отметить, что полученные результаты соответствуют критериям адекватности:
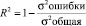> 0,96.
Дисперсию в данном случае определяют по формуле
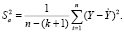
Проведённые расчёты F-теста также подтвердили адекватность модели результатам полученных дискретных данных.
Кроме этого, полученные спектры были восстановлены с помощью обратного преобразования Фурье. Полученные таким образом сигналы с хорошей точностью (R2 = 0,94) соответствовали исходным данным, как по амплитуде, так и по фазе.
Интерполированный сигнал был подвергнут преобразованию Фурье для выявления частот, характеризующих последовательную деполяризацию правого и левого предсердий и процесс быстрой реполяризации (расслабления) желудочков. На результатах спектрального анализа, представленных на рис. 2, зеленая линия, можно заметить два явно выраженных пика, с частотами w1 и w2. Вычислить принадлежность к определенному зубцу можно по стандартной формуле расчёта частот. Заметим, что отношение амплитуд пиков в спектре соответствуют отношению амплитуд зубцов кардиограммы.
Полученный результат говорит о том, что импульсы, отвечающие за деполяризацию предсердий и реполяризацию желудочков, генерируемые в синусо-предсердном узле, имеют разную природу и не связаны друг с другом. Однако зубцам P и T соответствуют по одной гармонике, следовательно, процессы, соответствующие зубцам, можно описать синусоидой. Также полученные в ходе эксперимента частоты примерно кратны двум. Такой показатель присущ многим биологическим автоколебательным системам [11].
После получения частот, соответствующим зубцам P и T, стояла задача поиска функциональных зависимостей между пиками на результатах спектрального анализа и зубцами кардиограммы. Для решения этой задачи применялся полосовой фильтр. Первым шагом было обнуление отдельных пиков спектра. Восстановленный сигнал лишь искажал форму зубцов комплекса QRS, не подвергая их полному удалению. Из этого следовал вывод, что ввиду формы остальных зубцов кардиограммы, отличной от синусоиды, им соответствует более одного пика спектра. Поэтому при дальнейшей фильтрации получалось более одной гармонической составляющей.
В дальнейшем полосовой фильтр включал в себя частоты от 0,3 Гц включительно до 3 Гц. Его применение позволило полностью убрать зубец R с кардиограммы. Полученный результат объясняется тем, что сокращение сердечной мышцы происходит достаточно резко. Зубец R характеризуется малым временем и резким всплеском разницы потенциалов. Такой процесс невозможно описать одной синусоидой, а следовательно, зубец характеризуется многими спектральными компонентами большой амплитуды и низкой частоты. При применении полосового фильтра к частотам от 3,2 Гц до 6,1 Гц было выявлено, что данная область соответствует зубцам Q и S. Зубцы имеют малые размеры и относительно неправильную форму, поэтому логично, что гармонические составляющие лежат в данной области.
Хочется отметить, что в ходе проведения эксперимента количество гармонических составляющих сигнала стандартной ЭКГ системы уменьшилось с 20 до 11. Девять гармоник рассматривались как паразитные, экспериментальным путем выявлены две частоты, соответствующие зубцам P и T, также выделено две области спектра, соответствующие зубцам R, Q и S (таблица).
Зависимость между частотами спектра и зубцами электрокардиограммы
|
Частота, Гц |
Зубец |
Описание |
|
0,3< |
– |
Низкочастотные неинформативные шумы |
|
0,3–3 |
R |
Зубец R характеризуется большой амплитудой за малый промежуток времени, поэтому ему соответствуют низкие частоты |
|
3,1 |
P |
Частота, полученная экспериментально |
|
3,1–6,2 |
Q + S |
Зубцы характеризуются маленьким временем и резким перепадом в данной области спектра. |
|
6,2 |
T |
Частота, полученная экспериментально |
|
>6,2 |
– |
Высокочастотные неинформативные шумы |
Выводы
В настоящей работе представлены результаты спектрального анализа сигнала первого отведения стандартной цифровой ЭКГ системы. С помощью обработки во временной области сигнал кардиограммы был очищен от шумов и наводок. В результате преобразования Фурье были получены спектры, которые содержали одиннадцать пиков, что примерно на девять меньше, чем при стандартной обработке.
Сглаживание δ-функции с последующей интерполяцией полиномом Лагранжа значительно уменьшает количество спектральных компонент и позволило выявить частоты w1 = 3,12 Гц и w2 = 6,21 Гц, соответствующих зубцам P и T. Оставшиеся частоты были классифицированы при применении полосового фильтра и поставлены в соответствие различным областям спектра кардиограммы. Таким образом выявлено, что зубцу R соответствуют гармоники с частотами от 0,3–3 Гц, а зубцам Q и S – 3,1–6,2 Гц.
Дальнейшая работа будет связана с выявлением зависимостей между каждым пиком спектра сигнала и зубцами временных зависимостей кардиограммы, а также определение взаимосвязей между заболеваниями сердечно-сосудистой системы и гармоническими составляющими сигнала. Важным шагом исследования спектров преобразованной кардиограммы является нахождение частот, соответствующие узкому и высокому пику R. Очевидно, что ввиду такой формы зубца в спектре ему соответствует сложная структура пиков.