В настоящей статье рассматриваются некоторые аспекты задачи выбора лучшего варианта, актуальность которых возникла в процессе решения задачи синтеза оптимальной цепочки операторов, образующих алгоритм обработки изображений изделий, находящихся на конвейерной ленте, с целью квалификации их качества [1–3]. Синтез цепочек осуществлялся с помощью модифицированного генетического алгоритма [1, 3], осуществляющего одновременно и структурную, и параметрическую идентификацию формируемого алгоритма. При этом требовалось обеспечить оптимальность алгоритма по двум критериям – быстродействию и точности вычислений. Это требование обусловило необходимость выбора и конкретизации метода оптимизации.
Задача выбора лучшего варианта предполагает наличие некоторого количества конкурирующих вариантов, каждый из которых характеризуется одним или несколькими показателями качества, которые могут называться частными критериями. При этом критерии характеризуются качественным направлением:
– критерий качественно положителен (имеет положительное качественное направление), если качество варианта тем больше, чем больше значение этого критерия;
– критерий качественно отрицателен (имеет отрицательное качественное направление), если качество варианта тем больше, чем меньше значение этого критерия.
Формирование множества конкурирующих вариантов и оценка их показателей качества является самостоятельной задачей, предшествующей задаче выбора варианта. Выбор лучшего варианта [3] заключается в определении варианта, который в некотором смысле лучше других вариантов.
Неопределенный термин «в некотором смысле» становится вполне определенным, если количество частных критериев равно одному: лучшим считается вариант с лучшим (наибольшим или наименьшим) значением критерия. В этом случае задача выбора варианта тривиальна и проблемы выбора не существует.
Проблема выбора имеет место, когда количество критериев не меньше двух, и именно при двух критериях эта проблема возникает. Суть проблемы такова: варианты, лучшие по частным критериям, – это в общем случае разные варианты. Преодоление этой проблемы невозможно без вовлечения экзогенной информации, безусловно связанной с субъективным взглядом на предметную область, в рамках которой решается задача выбора [4].
Рассмотрим задачу выбора лучшего (оптимального) варианта в условиях использования двух частных критериев для оценки качества конкурирующих вариантов [4, 5]:
Искомая величина:
k – ?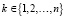 
,
Цель оптимизации выбора:
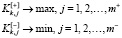
Ограничения:
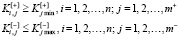
где k – номер искомого лучшего варианта; n – натуральное число, выражающее количество конкурирующих вариантов; m+, m– – натуральные числа, выражающие соответственно количество качественно положительных и качественно отрицательных критериев;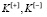 
– качественно противонаправленные частные критерии; 
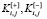– значения j-х частных критериев, соответствующих i-му варианту; 
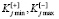– соответственно минимальное и максимальное значения j-х частных критериев.
В общем случае рассматриваемая задача не имеет точного решения, поскольку максимумы и минимумы разных частных критериев в общем случае соответствуют разным вариантам.
Цель исследования возникла в процессе решения задачи синтеза оптимальной цепочки операторов, образующих алгоритм обработки изображений изделий, находящихся на конвейерной ленте, и заключается в поиске наиболее рациональных способов решения следующих «классических» проблем, связанных с применением интегрального критерия в процедурах выбора «лучшего» варианта:
1) проблема разных диапазонов значений частных критериев качества сопоставляемых вариантов;
2) проблема качественной разнонаправленности частных критериев;
3) проблема синтеза рациональной структуры интегрального критерия.
Проблемы вербальности и разной значимости частных критериев не рассматриваются, поскольку они не имели места в контексте проблемной задачи.
Материалы и методы исследования
Все возможные решения рассматриваемой задачи являются приблизительными и, соответственно, необъективными. Каждый из методов решения этой задачи основан на формализации субъективных представлений о целесообразном и рациональном (разумном). Субъект или коллектив, представления которого формализуются, называется лицом, принимающим решение (ЛПР). Поскольку формализация субъективного представления о целесообразном и рациональном, как правило, является составной процедурой метода решения задачи, то, естественно, многократные решения задачи в одних и тех же условиях, определяющих количество вариантов и конкретику значений частных критериев, но разными ЛПР (а иногда и с одним и тем же ЛПР) могут приводить к получению разных результатов.
При любой формализации субъективных представлений предполагается, что выполнены два предварительных этапа:
1) формирование множества исходных вариантов;
2) оценивание значений частных критериев исходных вариантов.
Далее целесообразно осуществить сокращение информационного пространства рассматриваемой задачи путем выполнения следующих этапов:
3) формирование множества допустимых вариантов;
4) формирование множества Парето.
Множество допустимых вариантов формируется путем удаления из множества исходных вариантов тех из них, которые не удовлетворяют ограничениям на значения частных критериев [5, 6]. Обратим внимание на срабатывание механизма многокритериальности при выполнении указанной тривиальной процедуры: даже если некоторый вариант является наилучшим по какому-либо критерию, он все равно исключается из рассмотрения, если хотя бы один из других критериев не удовлетворяет установленному ограничению.
Множество Парето формируется путём удаления из множества допустимых вариантов качественно эквивалентных (дублирующих) и доминируемых вариантов.
Два варианта качественно эквивалентны, если имеют равные значения соответствующих показателей качества (частных критериев).
Отношение доминирования обозначается так: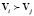 
. Говорят, что вариант Vi доминирует вариант Vj, и, соответственно, вариант Vj доминируется вариантом Vi, если одновременно справедливы следующие два условия:
1) среди показателей качества варианта Vi нет ни одного показателя, который был бы хуже соответствующего показателя варианта Vj;
2) хотя бы один из показателей качества варианта Vi лучше соответствующего показателя варианта Vj.
Таким образом, доминирующий и доминируемый варианты могут иметь равные показатели качества, но хотя бы по одному показателю первый лучше второго.
Множество Парето, состоящее из допустимых вариантов, само по себе представляет собой решение задачи выбора лучшего варианта. Причем это решение является точным, если множество Парето оказывается одноэлементным. Если же множество Парето состоит из нескольких элементов, то оно является решением «в первом приложении» и возможен поиск некоторого компромисса между значениями частных критериев, реализуемый на основе субъективных представлений о рациональном и целесообразном.
Результаты исследования и их обсуждение
Наиболее часто используемыми разновидностями формами интегрального критерия являются линейная и мультипликативная свертки [7, 8]. При использовании этих сверток приходится решать следующие проблемы:
1) разные диапазоны изменения разных критериев;
2) разное качественное направление критериев;
3) разные уровни значимости (важности) для ЛПР разных критериев;
4) лингвистические (словесные) значения некоторых частных критериев.
Первую проблему принято решать нормализацией – переходом от абсолютных значений критериев к относительным значениям, получаемым посредством операции деления.
Малорациональной представляется наиболее часто предлагаемая для практического использования в учебно-методической литературе [9] нормализация, совмещающая решение первой и второй проблем одновременно:
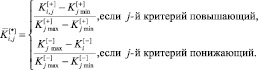(1)
Эта нормализация внешне эффектная: 1) она отображает значения всех частных критериев в один и тот же отрезок от нуля до единицы; 2) автоматически решает проблему разной качественной направленности критериев (все нормализованные критерии можно суммировать со знаком плюс). Однако такая нормализация по принципу «два в одном» имеет крайне существенный недостаток – она устанавливает эквивалентность диапазонов изменения частных критериев. В то же время очевидно, что незначительные (пренебрежимо малые) изменения одного критерия (например, точности решения задачи) никак не могут быть эквивалентны существенным изменениям другого критерия (например, длительности решения этой задачи). Таким образом, указанная нормализация (1) порождает новую проблему, которую приходится решать с помощью дополнительных весовых коэффициентов:
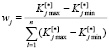, (2)
где wj – весовой коэффициент j-го частного критерия. Семантика указанных весовых коэффициентов такова: чем больше диапазон изменения частного критерия, тем выше его значимость. Таким образом, фактически нормализация (2) полностью решает только одну проблему – разной качественной направленности и только частично – проблему разных диапазонов изменения частных критериев. «Дорешивать» эту проблему приходится с помощью весовых коэффициентов (2).
Более рациональной представляется нормализация критериев их максимальными значениями:
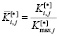(3)
где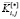 
, 
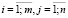– нормализованное значение j-го критерия i-го варианта; 
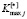– максимальное значение j-го критерия среди всех вариантов; n – количество частных критериев; * – символ качественного направления частного критерия:
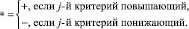
Нормализацию (3) можно рассматривать как установление эквивалентности максимальных значений критериев: максимальные значения всех нормализованных критериев оказываются одинаковыми – равными единице.
Вторую проблему рациональней всего решать путем суммирования качественно отрицательных критериев со знаком минус в аддитивной свертке и путем размещения этих критериев в знаменателе мультипликативной свертки.
Аддитивная свертка равнозначных критериев, нормализованных максимальными значениями (1), имеет вид
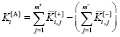, (4)
где m+, m– – соответственно количество повышающих и понижающих критериев.
Аналогичная мультипликативная свертка имеет вид
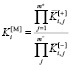. (5)
Существенным семантическим недостатком сверток (4) и (5) является их абсолютное базирование нулем – отсчет значений критериев начинается с нуля. В то же время очень часто ноль является либо физически, либо логически (согласно ограничениям) недостижимым значением. В таких случаях базирование значений нулем приводит к снижению их сопоставимости, – например, некорректно сравнивать фактические массы продуктов по их массе с упаковкой (брутто). Поэтому более целесообразным является базирование критериев их минимальными значениями во множестве Парето. При этом аддитивная и мультипликативная свертки приобретают вид
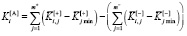, (6)
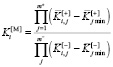. (7)
Теоретически, а иногда и практически интересным является частный случай – двух качественно противонаправленных критериев, т.е. когда m+ = 1, m– = 1. В теоретическом плане случай с двумя частными критериями показывает проблему формальной неразрешимости задачи выбора наилучшего варианта в рафинированном виде, подобно тому, как испытания Бернулли с двумя исходами иллюстрируют семантику принципа стохастичности наиболее четко и наглядно. Противонаправленность двух частных критериев позволяет рассматривать и сравнивать в «чистом» виде различные подходы к преодолению проблемы качественной противонаправленности применяемых показателей качества вариантов.
В практическом плане проблема выбора варианта с двумя частными критериями качества наиболее актуальна в задачах сопоставления различных алгоритмов решения задач: очень часто алгоритмы сравниваются по двум качественно противонаправленным критериям: точности и оперативности решения некоторой задачи. При этом качественно положительный критерий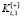 
имеет семантику точности вычислений, а качественно отрицательный критерий 
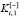имеет семантику времени вычислений. Мультипликативная свертка двух частных критериев вида (7) имеет вид
, 
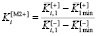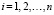. (8)
Семантически интегральный критерий (8) представляет собой прирост «производительности»: он показывает, насколько увеличивается (по отношению к минимальному значению) точность вычислений при увеличении на единицу времени вычислений. Верхний индекс [M2+] символизирует мультипликативность, двухкритериальность и тот факт, что свертка создана для поиска максимума прироста «производительности» (в числителе формулы размещено приращение качественно положительного частного критерия).
Применение свертки (8) при решении практической задачи синтеза оптимальной цепочки алгоритмов для вычисления градиентных изображений изделий по их фотографиям [3] привело к получению следующего наблюдения: максимум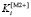 
«тяготеет» к начальной части упорядоченного множества допустимых вариантов, образующих множество Парето. Предпочтительными оказываются алгоритмы со значениями частных критериев, близкими к минимальным значениям (естественно, допустимым).
По этой причине был предложен и использован альтернативный интегральный критерий:
, 
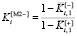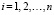. (9)
Заметим, что единицы в числителе и знаменателе (9) – это максимальные значения нормализованных значений частных критериев: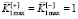 
, т.е. (9) можно записать и так:
, 
.
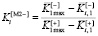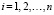Семантически интегральный критерий (9) отражает уменьшение затратности: он показывает, насколько сокращается (по отношению к максимальному значению) время вычислений при уменьшении на единицу точности вычислений. Минус в индексе [M2–] символизирует тот факт, что в числителе формулы размещено уменьшение качественно отрицательного частного критерия. Эта свертка создана для поиска максимума сокращения временных затрат за счет точностных потерь.
Применение свертки (9) при решении задачи синтеза оптимальной цепочки алгоритмов для вычисления градиентных изображений привело к получению следующего наблюдения: максимум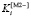 
«тяготеет» к конечной части упорядоченного множества Парето. Предпочтительными оказываются алгоритмы со значениями частных критериев, близкими к максимальным значениям. В упоминаемой задаче синтеза цепочки алгоритмов свертка (9) представляется более целесообразной по сравнению (8), поскольку она позволяет выбрать наиболее производительный алгоритм при незначительных потерях точности вычислений. В то же время свертка (8) может оказаться более предпочтительной при существенной абсолютной трудоемкости исследуемых алгоритмов.
Заметим, что обе свертки, и (8), и (9), представляют собой отношение некоторого выигрыша к ассоциированному проигрышу, т.е. конструкцию типа win / loss, которую можно назвать относительным преимуществом. В (8) числитель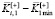 
представляет собой выигрыш по точности вычислений, а знаменатель 
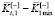– проигрыш по времени счета. В (9) числитель 
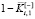представляет собой выигрыш по времени счета, а знаменатель 
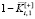– проигрыш по точности вычислений. При этом обе свертки выражают некоторый рациональный компромисс между двумя критериями, используемыми для выбора лучшего варианта.
На основе указанных сверток можно предложить следующее правило выбора лучшего варианта, которое имеет вид: в качестве лучшего варианта по двум качественно противонаправленным критериям следует принять вариант, входящий во множество Парето и имеющий максимум относительного преимущества в этом множестве. Значение качественно положительного критерия, соответствующее максимуму относительного преимущества, назовем рациональным максимумом, соответствующее значение качественно отрицательного критерия назовем рациональным минимумом.
Иллюстративный пример. На рисунке приведен график зависимости точности вычислений от времени счета пятнадцати алгоритмов, синтезированных с помощью генетического алгоритма [3], вошедших в динамическое множество Парето.
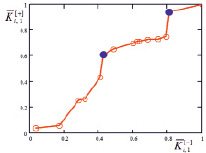
Зависимость точности вычислений от временных затрат
Кружочки на графике соответствуют алгоритмам, вошедшим во множество Парето. По оси абсцисс отложено нормализованное время работы алгоритма – реальное время, поделенное на максимальное значение времени счета среди алгоритмов, вошедших во множество Парето. По оси ординат отложена нормализованная точность алгоритма (коэффициент корреляции) – реальный коэффициент, поделенный на максимальное значение коэффициента среди алгоритмов, вошедших во множество Парето.
Вектор значений интегрального критерия (8):
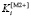= [1; 0.1387; 0.8608; 0.7931; 1.053; 1.45; 1.355; 1.164; 1.141; 1.114; 1.059; 0.9733; 0.9319; 1.164; 0.9947]
Графически каждое значение вектора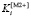 
– это тангенс угла наклона к оси абсцисс прямой, соединяющей начальную и текущую точку графика.
Вектор значений интегрального критерия (9):
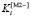= [1.005; 0.8815; 0.9604; 0.9265; 1.044; 1.46; 1.471; 1.324; 1.306; 1.257; 1.159; 0.9488 0.8161; 3.281; 1]
Графически каждое значение вектора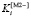 
– это тангенс угла наклона к оси ординат прямой, соединяющей текущую и конечную точку графика.
Рассматривая значения векторов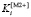 
и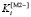 
, можно установить, что согласно критерию (8) лучшим является шестой алгоритм, а по критерию (9) – четырнадцатый.
Заключение
1. При решении проблемы разных диапазонов значений частных критериев процедура нормализации рассмотрена как процесс установления эквивалентности между нормализованными значениями. Показана целесообразность нормализации частных критериев их максимальными значениями (3). Указаны недостатки широко применяемой нормализации отрезками значений (2).
2. Проблема качественной разнонаправленности частных критериев решена использованием мультипликативной формы свертки этих критериев со следующей семантикой – в числителе размещается выигрыш, а в знаменателе проигрыш от отклонений критериев от их максимальных значений (единицами в нормализованном представлении).
3. При решении проблемы выбора структуры свертки частных критериев предпочтение отдано мультипликативной форме, но этот факт не является принципиальным, – все последующие предложения могли бы быть представлены и в аддитивной форме.
4. Предложена семантически оригинальная структура мультипликативной свертки (9), отличающаяся тем, что в ней в качестве выигрыша используется преимущество, получаемое от уменьшения качественно отрицательного критерия, а в качестве проигрыша – ущерб от уменьшения качественно положительного критерия. Назовем эту структуру структурой B. Структуры с традиционной семантикой (8), в качестве выигрыша используют увеличение положительно направленного критерия, а в качестве проигрыша – увеличение критерия с отрицательным качественным направлением. Назовем структуру с классической семантикой структурой A.
5. Показано отличие сверток критериев со структурами А и B – первая «тяготеет» к минимальным значениям качественно отрицательного критерия, а вторая – к максимальным значениям качественно положительного критерия.
6. В рамках решения задачи автоматического синтеза алгоритма по двум качественно разнонаправленным критериям могут использоваться как предложенная структура B, так и классическая структура A в зависимости от абсолютных значений того или иного критерия.