В познании жизни, окружающего мира и общества классификационные методы играют ведущую роль. В определенном смысле можно утверждать, что классифицировать – значит познать. Хорошо известна роль гениальных классификаций в развитии человеческих знаний, например, стратиграфической шкалы, периодической системы химических элементов, классификаций биологических видов, горных пород, подземных вод и многих других.
Получая новую информацию, исследователь часто сталкивается с проблемой построения новой классификационной структуры наблюдений. Для решения этой задачи необходима эффективная цифровая компьютерная технология построения классификации многомерных наблюдений. При выделении однородных частей объектов, явлений и процессов появляется возможность обоснованно применить математико-статистические методы их объективной характеристики, а сравнением однородных частей – открывать новые закономерности их формирования.
По теории и методам классификации многомерных наблюдений имеются сотни работ, в которых предлагается использование кластерного анализа, применение алгоритмов классификации в условиях наличия априорной информации о классификационной структуре наблюдений (задача с учителем) и в меньшей степени задача самоорганизации (без учителя). Одной из первых работ в области распознавания образов считают исследования Ф. Розенблата по созданию персептрона в 1950-е гг. В России различным методам классификации наблюдений и распознавания образов посвящены сотни публикаций [1–3]; в области классификации геологических данных также выполнены многочисленные исследования [4–6].
Столкнувшись с проблемой обобщения геохимической информации по Уральскому региону (сотни тысяч анализов и тысячи геохимических аномалий), автор пришел к выводу о необходимости разработки новой классификационной технологии. Эта технология получила название G-метод, использована при обосновании многих научных и прикладных вопросов и опубликована более чем в 200 работах в России и за рубежом [6–8].
Одна из первых работ автора по проблемам построения классификации геологических данных опубликована в журнале «Геология и геофизика» [9]. Основная идеология нового критерия была представлена в кандидатской диссертации «Вопросы методики и некоторые результаты применения математической статистики и ЭЦВМ при гидрогеохимических исследованиях (на примере Урала)». В настоящей работе автор излагает краткий вывод критерия, основные положения классификационной технологии и некоторые примеры их использования.
Вывод критерия
При выводе формулы Z2 для зависимых наблюдений и признаков нами использован прием преобразования числа зависимых наблюдений (N) в статистически эквивалентное число независимых (n), предложенный А.А. Багровым [3], который показал, что
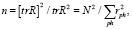
где rph – коэффициент корреляции между наблюдениями p и h, tr R – след матрицы R.
Эту формулу определения эквивалентного числа независимых наблюдений n по числу зависимых N мы использовали для обоснования критерия Z2 [5, 6, 8].
Воспользовавшись условием эквивалентности, можно записать
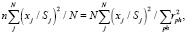
где xj – значение наблюдения j; Sj – среднеквадратичное отклонение.
Но первая часть этого уравнения имеет распределение χ2 с числом степеней свободы f = n, следовательно, величина
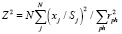
также имеет распределение χ2 c
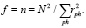
Переходя к более общему случаю, когда среднее не равно нулю, можно записать аналогичную процедуру для зависимых признаков М и независимых наблюдений N, воспользовавшись формулой эквивалентности
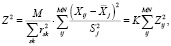
f = K?M?N,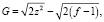 
где Xij – значение признака j в наблюдении i;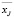 
, Sj – среднее и стандартное отклонение признака j; rsk – коэффициент корреляции между признаками s и k; М – число признаков; N – число наблюдений; f – число степеней свободы; G – преобразование распределения χ2 к нормальному с параметрами (0,1). Если вычисленное G > Gq, то наблюдение (или N наблюдений) по M признакам не принадлежит данному однородному классу наблюдений с уровнем значимости q.
Последняя ситуация (независимые наблюдения и зависимые признаки) очень часто встречается на практике и поэтому рассмотрим ее наиболее подробно.
Если признаки функционально зависимы, то все rsk = 1 и коэффициент K = 1/M;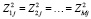 
и тогда
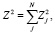
с числом степеней свободы f = N.
Это означает, что мы имеем дело только с одним независимым признаком.
Если признаки независимы, т.е. rsk = 0 при s ≠ k и rsk = 1 при s = k, то K = 1 и тогда
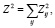f = MN.
Получен тривиальный случай для независимых признаков.
Таким образом, последняя формула справедлива и для крайних случаев, когда величины зависят функционально или независимы.
Метод классификации многомерных наблюдений
При изучении природных объектов, явлений и процессов широко применяются различные модификации кластерных построений, выделения однородных статистических совокупностей, факторного анализа, процедуры распознавания образов, которые позволяют выделить некоторые однородные по заданному комплексу признаков части объектов и далее проводить анализ закономерностей их формирования.
Среди методов классификации многомерных наблюдений выделяются три главные группы:
1) построение классификации в условиях неопределенности (задача без учителя);
2) построение классификации при наличии некоторых априорных данных;
3) классифицирование новых наблюдений по известной классификации.
Формально задача построения классификации может быть сформулирована следующим образом: множество наблюдений N, каждое из которых охарактеризовано М признаками, необходимо разделить на подмножества – однородные таксоны, внутри которых наблюдения близки между собой, а таксоны максимально различаются.
В основу рассматриваемой классификационной процедуры положен описанный критерий Z2, позволяющий использовать зависимые признаки. Проверяется нулевая гипотеза (Но) об отсутствии различий между множеством многомерных наблюдений и данной статистической совокупностью, т.е. гипотеза о принадлежности многомерных наблюдений к данному однородному таксону.
На основе оригинального критерии Z-квадрат развит новый цифровой компьютерный G-метод [5, 6, 8] классификации многомерных наблюдений, в котором удалось реализовать большинство указанных выше важных особенностей: построение классификации в условиях самоорганизации (задача без учителя); использование зависимых признаков; неограниченное соотношение между числом наблюдений (N) и числом признаков (М); выделение таксонов различных уровней; оценка сходства-различия между однородными таксонами по каждому признаку и по сумме признаков и другие.
Процедура цифровой компьютерной классификационной технологии сводится к следующим операциям: выбирается исходная система координат; отыскивается центр первого однородного таксона и все наблюдения этого таксона; выполняется повторение указанных операций для наблюдений, не вошедших в предыдущие однородные таксоны.
Создано несколько вариантов компьютерных программ реализующих G-метод (Оптим, Анатф, G-mode, AGAT и др.). Наиболее эффективной оказалась программа AGAT-2 (Свидетельство о государственной регистрации программы № 2008615215 от 29 октября 2008 г.), позволяющая автоматически строить классификации многомерных наблюдений различного уровня детальности.
Примеры применения классификационной технологии
Цифровая компьютерная технология классификации многомерных наблюдений (G-метод) успешно применена при изучении природных и антропогенных систем на Земле, Луне, Марсе, Юпитере, кометах, астероидах и в дальнем космосе. По результатам этих исследований опубликовано более 200 работ, в том числе более 100 в России и за рубежом в соавторстве с итальянскими, французскими, немецкими и американскими коллегами [5, 6, 8].
Ниже рассмотрены отдельные примеры практического применения цифровой компьютерной технологии G-метод при построении классификаций объектов, явлений и процессов и описания закономерностей их формирования.
Классификация лунных пород и стекол
При построении классификации лунных пород и стекол по химическому составу использовано более 2500 анализов образцов, доставленных автоматическими станциями «Луна-16 и 20» и астронавтами кораблей «Аполлон-11, 12, 14, 15, 16 и 17». Для каждой из космических экспедиций были составлены классификации образцов по составу породообразующих окислов [5, 7]. Обобщение всех классификаций позволило уверенно выделить семь главных групп лунных пород:
1. Анортозиты (габбро-анортозиты).
2. Материковые базальты (полевошпатовые базальты, анортозитовые габбро).
3. Криповые базальты (KREEP, базальты Фра Мауро).
4. Габбро-базальты (морские базальты Моря Изобилия).
5. Морские базальты (базальты Океана Бурь и Моря Дождей).
6. Высокотитанистые морские базальты (базальты Моря Спокойствия).
7. Калиевые граниты (высококремнистые породы).
Группы объединены в три типа. Первый тип – анортозитовые породы – является материковым веществом. Ко второму типу отнесены пять групп базальтов, которые образовались позднее первого типа при излиянии расплавов вещества на поверхность. Третий оригинальный по составу тип обнаружен впервые авторами и соответствует калиевым гранитам, которые могут быть остаточным материалом после отделения базальтов. Наличие значительного количества калиевых гранитов на Луне может сильно повлиять на существующие представления о ее элементарном составе, так как с указанными породами могут быть связаны повышенные концентрации многих элементов, которые сейчас относят к потерянным в процессе аккреции.
Изучение поверхности Марса
G-метод применен при построении классификации топографической поверхности Марса [10] по данным Марсианского орбитального лазерного альтиметра (MOLA). В качестве главных признаков использованы средние квадратичные отклонения высоты и уклонов и экспонента Харста (Hurst). Выявлено, что параметр «среднее квадратичное отклонение высот» резко различен для северного и южного полушарий Марса, в то время как экспонента Харста имеет выраженный широтный тренд. Классификация наблюдений выявила 29 однородных таксонов, некоторые из них имеют четкую корреляцию с геологическим строением планеты, другие – коррелируются с широтным трендом.
Изучение спутника Сатурна Феба
Для изучения состава поверхности спутника Сатурна Феба использованы спектральные данные, полученные космической экспедицией Кассини (Cassini) с помощью спектрометра VIMS. Феба, по мнению многих астрономов, является внешним телом, захваченным гравитацией Сатурна из пояса Купера, поэтому он характеризуется оригинальным составом и строением. По результатам классификации спектральных данных [11] установлено, что помимо крупных таксонов, характеризующих основную часть поверхности спутника, которая сложена каменно-ледяным материалом, выделены оригинальные классы, свидетельствующие о наличии участков, где коррелируются высокие содержания H2O и CO2 (газ заключен во льду) и где CO2 не коррелируется с H2O. Это может свидетельствовать о наличии оригинальных процессов на Фебе.
Изучение гидрогеохимических закономерностей
Значительные объемы исследований и количество публикаций посвящены проблемам изучения закономерностей формирования химического состава шахтных, грунтовых и поверхностных вод Восточного Донбасса [5, 6, 8]. При обобщении гидрогеохимической информации использовано более 2000 анализов вод за столетний период (с 1920 по 2015 г.).
Типы изменения состава шахтных вод. С помощью G-метода выделено четыре главных гидрогеохимических типа изменения химического состава шахтных вод по результатам опробования в 1923, 1967, 1992 и в 2015 гг. [8]. Первый тип – это слабокислые (величина pH соответственно составила 4,4; 4,5; 6,0 и 5,7) сульфатные магниево-кальциево-натриевые воды с минерализацией 4,6; 4,4; 4,5 и 5,7 г/л. Второй – нейтральные (величина pH – 7,3; 7,8; 7,6 и 6,7) хлоридно-сульфатные натриевые воды с минерализацией 3,9; 3,9; 4,2 и 7,6 г/л. Третий тип (отсутствует в 2015 г.) – нейтральные (pH – 7,0; 6,9 и 7,8) сульфатно-хлоридные натриевые воды с минерализацией 3,2; 3,0 и 5,1 г/л. Четвертый – нейтральные (pH – 7,6; 7,7; 7,6 и 7,3) гидрокарбонатно-сульфатно-хлоридные натриевые (содовые) с минерализацией 3,2; 2,9; 4,5 и 2,7 г/л.
Наиболее интересные генетические выводы связаны с первым и четвертым типами. Первый тип характеризуется преобразованием исходных слабоминерализованных вод в кислые сульфатные воды с высокими содержаниями Fe, Al, Cu, Pb, Co и других металлов, что обусловлено интенсивным развитием процессов окисления серы и сульфидов. Воды первого типа формируют наиболее интенсивные потоки загрязнения природных вод региона [12, 13].
Четвертый тип формирования химического состава шахтных вод – это оригинальные содовые гидрокарбонатно-сульфатно-хлоридные и хлоридные натриевые воды с высокими содержаниями НСО3 и очень низкими Ca и Mg. В горные выработки поступают содовые подземные воды, которые образуются в результате испарительно-конденсационных процессов в водоуглеродной газовой фазе (обратная вертикальная геохимическая зональность подземных вод региона). Автор делает прогноз [5, 6, 8], что в районе угольных шахт, где обнаружены содовые воды четвертого типа, наиболее высоки перспективы обнаружения нефтегазовых месторождений, например, в структурах Гуково-Зверевского угленосного района.
Заключение
В познании жизни, общества и окружающего мира классификационные методы играют ведущую роль. Получая новую информацию, исследователь обычно сталкивается с проблемой построения новой классификационной структуры наблюдений для обнаружения и описания ранее не известных закономерностей.
Вывод формулы описанного критерия Z2 для зависимых наблюдений и признаков выполнен с использованием способа преобразования числа зависимых наблюдений (N) в статистически эквивалентное число независимых (n), предложенного А.А. Багровым.
На основе оригинального критерии Z-квадрат развита и применена новая цифровая компьютерная технология – G-метод классификации многомерных наблюдений, который обладает такими важными свойствами, как построение классификации в условиях неопределенности (задача без учителя); использование зависимых признаков; оценка сходства-различия между однородными таксонами, выделение таксонов различного уровня и другими.
Цифровая компьютерная классификационная технология (G-метод) успешно применена при изучении объектов, явлений и процессов на Земле, Луне, Марсе, Юпитере, кометах, астероидах и в дальнем космосе. Например, применение указанной технологии при изучении лунных пород и стекол позволило построить их классификацию по химическому составу, изучить связь особенностей поверхности Марса с его геологическим строением, установить зависимость цвета поверхности спутника Сатурна Феба от его состава, описать закономерности формирования химического состава шахтных и подземных вод Восточного Донбасса.
Автор выражает благодарность за помощь в проведении исследований Международной программе «Эразмус. Минерал+», «Модернизация геологического образования в российских и вьетнамских университетах».