В данное время вопрос о нахождении собственных чисел и собственных векторов приобретает огромное значение. Таким образом, появились новые численные методы для нахождения собственных характеристик абстрактных операторов. В 1894 г. французским ученым Анри Пуанкаре на частном примере рассмотрена аналогия алгебраической задачи к теории краевых задач математической физики. Установление этой аналогии способствовало зарождению аналитической теории собственных значений. А в 1957 г. получен новый метод приближенного вычисления собственных чисел оператора Штурма – Лиувилля. Создателями данного метода явились такие великие математики XX в., как И.М. Гельфанд и Л.А. Дикий. Позднее, в 1995 г., С.А. Шкариным доказано, что данная система бесконечных линейных уравнений определенного типа имеет не только единственное решение. Это утверждение повлекло появление собственных чисел операторов, которые получились благодаря созданию класса особых операторов, который ввели В.А. Садовничий и В.Е. Подольский. Таким образом, математики доказали возможность решения данного класса задач с заданной погрешностью вычисления. После высказанных утверждений возникло много работ по данной проблематике [1, 2]. Для того чтобы распространить полученные результаты и в другие науки, потребовалось изучение спектральной теории дифференциальных операторов. В результате чего некоторые задачи аналитически решить так и не удалось [3], это привело к созданию определенных численных методов [4, 5].
Цель исследования: рассмотреть методы нахождения собственных значений операторов, такие как метод А.Н. Крылова и метод QR-разложения, осуществить программную реализацию и сравнительный анализ.
Материалы и методы исследования
Вычисления проводились на программной платформе .NET Framework 4.5.1, в качестве IDE использовалась Microsoft Visual Studio 2017.
Рассмотрим решение задачи нахождения собственных значений матрицы
методами А.Н. Крылова и методом QR-разложения с заданной точностью.
Результаты исследования и их обсуждение
Метод А.Н. Крылова
Для этого сначала выберем начальный вектор: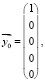 
тогда
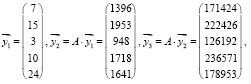
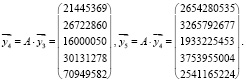
Система для нахождения p1, p2, p3, p4 будет выглядеть следующим образом:
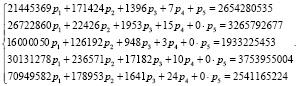
Данная система алгебраических уравнений решается с помощью точных методов. СЛАУ можно решить методом Гаусса или Крамера. Далее получим
p1 = 189, p2 = –8992, p3 = 103138, p4 = 919881, p5 = –7869413.
Следственно, характеристическое уравнение для матрицы A будет выглядеть так:
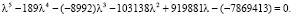
Корни характеристического уравнения будут следующие:
λ1 = 123,324, λ2 = 28,3403, λ3 = 40,0631, λ4 = –8,98375, λ5 = 6,25585.
Метод QR-разложения
Для нахождения собственных значений можно воспользоваться методом QR-разложения. Суть данного метода в преобразовании Хаусхолдера. Таким образом, необходимо все элементы матрицы, которые находятся ниже ее главной диагонали, обратить в нуль.
Осуществляется данный процесс с использованием матриц Хаусхолдера по следующей формуле:
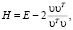
здесь υ – случайный ненулевой вектор-столбец, E – единичная матрица заданной размерности и υυT – квадратная матрица также заданной размерности.
В завершении данного процесса получим квадратную матрицу, элементами которой являются вещественные числа. Кроме того, элементы матрицы, расположенные симметрично ее главной диагонали, одинаковы. Заметим также, что результат умножения полученной матрицы на транспонированную ей матрицу равен единичной матрице. Далее берем вектор v случайным образом. В связи с этим будут иметь место дополнительные требования к построенной матрице [6].
Для получения вектора, все элементы которого равны нулю за исключением первого элемента, необходимо воспользоваться следующей формулой:
, 
.
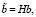
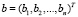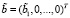Тем самым будет построена матрица Хаусхолдера. Далее для нахождения вектора v воспользуемся формулой
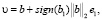
где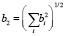 
– норма вектора евклидова пространства, 
.
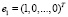Алгоритм повторяется многократно, пока не будет достигнута цель, а именно получение нулевых элементов матрицы, расположенных ниже ее главной диагонали. Таким образом, требуемое разложение будет получено за определенное число шагов.
Остановимся на более подробном описании и детальном анализе указанного процесса. Для этого возьмем A0 = A. Далее выполним преобразование Хаусхолдера H1(A1 = H1A0). Последнее позволит получить из матрицы A0 новую матрицу A1, у которой все элементы первого столбца, расположенные под главной диагональю, равны нулю:
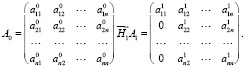
Первый столбец преобразованной матрицы равен H1. В данном случае произведем замену вектора на выражение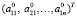 
.
Далее необходимо воспользоваться формулой для поиска вектора:
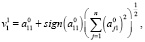
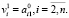
Матрицу Хаусхолдера можно найти по следующей формуле:
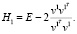
Второй шаг состоит в преобразовании матрицы H2(A2 = H2A1) так, чтобы получилось обнуление элементов, которые находятся ниже главной диагонали второго столбца матрицы A1. Для этого необходимо взять новый вектор размерности n-1, который будет равен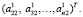 
Тем самым, получим
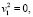
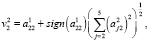
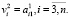
Для того чтобы получить искомое выражение, необходимо повторять данный процесс n-1 раз:
A = QR,
где
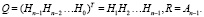
Алгоритм Гаусса и преобразование Хаусхолдера во многом идентичны. Различие методов состоит в получении нулевых элементов, находящихся под главной диагональю матрицы [7].
Данное преобразование неоднократно встречается в процессе нахождения собственных значений. Применим его при построении итерационного процесса. Для этого воспользуемся формулами
…
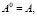
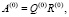
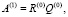
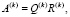
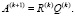
Осуществление итерационного процесса происходит в несколько этапов, а именно:
1. Умножение матрицы A(k), ортогональной Q(k) и верхней треугольной R(k).
2. Умножение матриц с конца. Данный этап получится в том случае, если матрицы согласованы.
Схожесть объектов A(k) и A(k+1) не сложно заметить в том случае, если учитывать ортогональность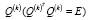 
. Данное утверждение можно записать в следующей символьной форме:
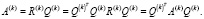
Таким же образом можно показать, что результат умножения транспонированной матрицы на первоначальную будет равен единичной матрице. Для получения верхней треугольной матрицы необходимо проверить отрицание кратных значений.
Вещественные значения получаются при обнулении поддиагональных элементов. Появление комплексных значений возможно, если при проверке оказывается, что данные числа действительные, а также их можно преобразовать к верхней треугольной матрице.
Для проверки достижения заданной точности используют формулу
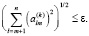
В результате собственные значения равны диагональным элементам. Матрица A(k) имеет квазидиагональную матрицу из-за соответствия диагонального блока, соответствующей размерности 2 на 2, который отвечает комплексно сопряженным значениям. Элементы таких блоков терпят преобразование в ходе итерационного процесса. При этом полученный ряд, состоящий из комплексных значений, сходится. В процессе организации данного процесса возможно появление комплексно-сопряженной пары значений, которая при помощи j-го и (j + 1)-го столбцов с элементами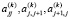 
несколько изменяет ход решения. Однако, учитывая квадратное уравнение 
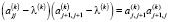, можно заметить, что элементы уравнения, начиная с некоторого номера, меняются не так явно. Для окончания итерационного процесса используется формула
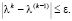
Многократные вычисления, которые необходимы для QR-факторизации матрицы, являются существенным недостатком.
Однако количество итераций можно существенно сократить, для этого необходимо внести изменения в начальную матрицу. А именно преобразовать ее в матрицу
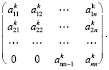
Таким образом, эффективность QR-алгоритма может быть повышена [8].
Проанализируем:
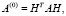
где A(0) – матрица Хессенберга, которая имеет следующую структуру.
где знак x – это отличная от нуля составляющая.
Для более экономичного процесса QR-разложения на протяжении циклического процесса матрицы A(k) необходимо сохранять треугольную матрицу, которая находится над главной диагональю [9].
Определяем матрицу A(i) и сравниваем с заданной точностью. Процесс продолжается пока точность матрицы не станет меньше либо равной заданной точности. При помощи программы написанной на Maple, поддиагональные элементы меньше заданной точности оказываются на восемнадцатом шаге и условие сходимости выполняется.
Найдем собственные значения [10]. Первое собственное значение будет равно элементу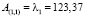 
. Для последующего нахождения собственных значений воспользуемся формулой
.
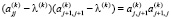В том случае, когда возьмем j = 2, получим два квадратных уравнения, из которых найдем собственные значения, которые будут равны
λ2 = 28,337, λ3 = 40,059.
Аналогично найдем λ4 и λ5, при подстановке в формулу j = 4:
λ4 = –8,9800 и λ5 = 6,2503.
В итоге получили следующие собственные значения:
λ1 = 123,37, λ2 = 28,337, λ3 = 40,059, λ4 = –8,9800, λ5 = 6,2503.
Выводы
Для сравнительного анализа по очереди вычислим собственные значения матрицы с помощью метода А.Н. Крылова и метода QR-разложения. Результаты вычислений занесены в таблицу.
Таблица собственных значений матрицы 5х5
|
№ п/п |
Метод А.Н. Крылова |
Метод QR-разложения |
Абсолютная погрешность |
|
1 |
123,324 |
123,37 |
0,04600 |
|
2 |
28,3403 |
28,357 |
0,01670 |
|
3 |
40,0631 |
40,059 |
0,00410 |
|
4 |
–8,98375 |
–8,9800 |
0,00375 |
|
5 |
6,25585 |
6,2503 |
0,00555 |
Изучив подробно методы А.Н. Крылова и QR-разложения и применив их к нашей матрице, можно сделать вывод о том, что: при нахождении собственных значений оба метода дают приблизительно один результат, но все же имеется различие на некоторые доли.
Высокая точность и достаточно простая реализация делают методы А.Н. Крылова и QR-разложения достаточно распространенными методами нахождения собственных значений.