В настоящее время в швейной промышленности широкое применение находят технологии безниточного соединения деталей кроя [1–3]. К указанным технологиям относятся, например, такие способы соединения деталей, как термоклеевая сварка, сварка током высокой частоты, сварка горячим воздухом, термоконтактная сварка. Среди безниточных способов соединения материалов большое распространение получает ультразвуковая сварка, что вызвано увеличением использования в швейном производстве синтетических полимерных материалов [4]. Следует отметить, что ультразвуковая сварка также находит широкое применение в технологиях получения бесшовных изделий при изготовлении функционального белья [5] и изделий из волокнистых нетканых материалов [6]. Ультразвуковая сварка позволяет выполнять соединение деталей без использования вспомогательных материалов, обладает высокой производительностью и экологической чистотой технологических процессов. По способу выполнения сварного шва можно выделить три группы машин ультразвуковой сварки: последовательного прерывистого выполнения швов; последовательного непрерывного выполнения швов; параллельного выполнения швов (прессы). Машины для выполнения прерывистого шва являются наиболее универсальными, чаще всего [1] строятся на базе швейных машин и могут применяться в качестве их непосредственной замены. Особенностью машин ультразвуковой сварки прерывистого действия является наличие механизма привода пуансона, который периодически воздействует на свариваемые материалы и должен обеспечивать [1] необходимое усилие прижима материалов в зоне сварки, требуемую длительность выстоя пуансона во время сварки, заданную величину подъема пуансона над материалами, достаточную для транспортирования материалов.
Рассмотрим схему механизма привода пунсона [1, 7], представленную на рис. 1. В состав привода входит шестизвенный рычажный механизм, который преобразует вращение кривошипа 1 в возвратно-поступательное движение ползуна 5. Ползун 5 имеет возможность поступательного движения относительно пуансонодержателя 8, перемещающегося относительно неподвижной направляющей 7 и жестко соединенного с пуансоном 12. На пуансонодержателе 8 закреплен упор 9, положение которого может изменяться с помощью регулировочного винта 10. Между ползуном 5 и упором 9 установлена замыкающая пружина 11.
При движении ползуна 5 из крайнего верхнего положения вниз, пуансон 12, вместе с пуансонодержателем 8, также перемещается вниз под действием пружины 6 до тех пор, пока пуансон не опустится на материалы 13. После этого пуансон вместе с пуансонодержателем останавливается, ползун 5 продолжает перемещение относительно пуансонодержателя 8. В зону сварки подается ультразвук, при этом пуансон 12 должен оставаться неподвижным. Подъем пуансона 12 вместе с пуансонодержателем 8 осуществляется при движении ползуна 5 вверх после его контакта через пружину 11 с упором 9. В рассматриваемом механизме предусмотрена возможность регулирования величины усилия, создаваемого пуансоном при фиксации материалов в процессе сварки, с помощью изменения усилия предварительного поджатия пружины 6. Установкой упора 9, фиксируемого при помощи регулировочного винта 10 относительно пуансонодержателя 8, можно регулировать длительность выстоя пуансона при сварке.
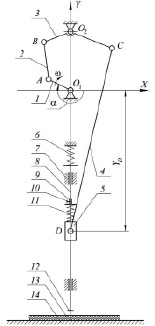
Рис. 1. Схема механизма
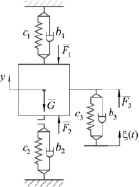
Рис. 2. Динамическая модель
Связь пуансона 12 с материалами 13 является неудерживающей. При этом требуется чтобы в момент сварки усилие между пуансонодержателем и материалами было постоянным. Наличие неудерживающей связи может приводить к возникновению нежелательных колебаний пуансона относительно материалов в период сварки, что в свою очередь, может сказываться на качестве шва. В настоящей статье рассматривается задача разработки динамической и математической модели механизма привода пуансона с целью исследования характера воздействия пуансона на свариваемые материалы и совершенствования механизма привода пуансона.
Материалы и методы исследования
Представим рассматриваемую механическую систему (рис. 1) в виде динамической модели на рис. 2. Будем считать пуансон 12, пуансонодержатель 8 и упор 10 (рис. 1) абсолютно твердым телом – «пуансон», имеющим возможность перемещаться вдоль направляющих по вертикали на величину y (рис. 2). Замыкающую пружину 6, свариваемые материалы 13, пружину 11 (рис. 1) представим на динамической модели (рис. 2) в виде упруго-диссипативных элементов с приведенными коэффициентами жёсткости ci и сопротивления bi,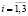 
соответственно. Неудерживающая связь «пуансона» с материалами на динамической модели представлена элементом «односторонняя неудерживающая связь». Обозначим ξ(t) – перемещение ползуна 5.
На «пуансон» действуют силы (рис. 2): F1 – сила со стороны пружины 6 (рис. 1); F2 – равнодействующая распределенных сил, в направлении оси O1Y (рис. 1) со стороны свариваемых материалов из-за их деформации под «пуансоном» на величину y (при y < 0 «пуансон» внедряется в материалы, при y < 0 «пуансон» перемещается над материалами); F3 – сила со стороны пружины 11 из-за ее деформации на величину Δ = ξ(t) – y из-за относительного движения ползуна 5 и пуансонодержателя 8 (рис. 1); G – сила тяжести «пуансона» (G = mg, m – масса «пуансона», g = 9,81 м/с2). Силу трения в поступательной кинематической паре между ползуном 5 и пуансонодержателем 8 будем считать малой и ниже не учитываем.
Математическая модель, соответствующая представленной на рис. 2 динамической модели «пуансона», с учетом принятых обозначений может быть представлена в виде
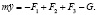(1)
Обобщенная координата y связана с перемещением ξ(t) ползуна 5 (рис. 1) и деформацией Δ пружины 11 следующим равенством
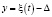. (2)
Запишем аналитические выражения входящих в (1) сил. Учитывая малость y, силу F1 можно записать в виде
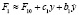, (3)
где F10 – сила, соответствующая начальному поджатию пружины 6 в установочном положении.
Силу F2, с учетом неудерживающей связи, приближенно [8, 9] запишем в виде
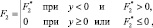(4)
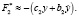(5)
Аналитическое выражение для силы F3 с учетом малости деформации Δ можно приближенно представить в виде
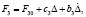(6)
где F30 – сила, соответствующая начальному поджатию пружины 11 в установочном положении, Δ = ξ(t) – y.
Зависимость ξ(t), представляющая собой кинематическое внешнее воздействие, может быть определена в результате кинематического анализа рычажного шестизвенного механизма [6], приводящего в движение ползун 5. Пусть YD(α) – функция положения ползуна 5 (шарнира D, рис. 1), где α = α0 – φ – угол поворота кривошипа O1A, α0 = const, φ = ωt, ω – угловая скорость вращения главного вала O1. Начальное значение угла α = α0 при t = 0 выберем так, чтобы оно соответствовало крайнему верхнему положению шарнира D. Введем функцию перемещения ψ(φ) ползуна 5, которую представим в виде
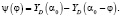
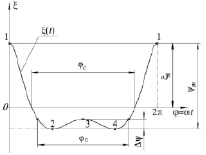
Рис. 3. Зависимость ξ(φ)
Функция перемещения ξ(φ) характеризует отклонение ползуна 5 от его крайнего верхнего положения. С учетом введенных обозначений зависимость ξ(t) может быть представлена в виде (рис. 3)
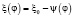, (7)
где ξ0 – максимальная величина подъема «пуансона» над материалами.
Следует отметить, что функция перемещения ψ(φ) может быть задана в виде требуемой функции перемещения [7] ползуна 5, с учетом задаваемых конструктором значений: ψm – максимального перемещения ползуна 5; φ0 – длительности выстоя, Δψ – точности воспроизведения выстоя. Изменением величин φ0 и ψm можно устанавливать длительность сварки материалов φc.
Будем считать, что при t = 0 «пуансон» находится в крайнем верхнем положении, при этом Δ = 0 (установочное положение). Имея в виду, что в крайнем верхнем положении «пуансона» ξ(0) = ξ0, получим
при t = 0: y(0) = ξ0,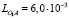 
. (8)
Таким образом, дифференциальное уравнение (1) при учете (8), (2)–(7) представляет собой математическую модель «пуансона».
Результаты исследования и их обсуждение
Для численного решения дифференциального уравнения (1) удобно воспользоваться функцией ode45( ) входящей в состав среды MATLAB [10]. С использованием разработанной в среде MATLAB программы было выполнено математическое моделирование колебаний «пуансона». В процессе моделирования использовались следующие исходные данные: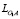 
= 6,0•10-3 м, LAB = 39,0•10-3 м, 
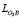= 10,0•10-3 м, 
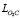= = 7,1•10-3м, LCD = 65,0•10-3 м, 
, 
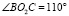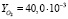м, ξ0 = 4,5•10-3 м, m = 0,063 кг, F10 = 20 Н, c1 = 2000 Н/м, b1 = 0,71 Н/(м/с), c2 = 5,0•104 Н/м, b2 = 97,64 Н/(м/с), c3 = = 1,0•105 Н/м, b3 = 7,10 Н/(м/с), F30 = 0 Н. В результате вычислений разработанная программа выводит графики зависимостей y(t), 
, 
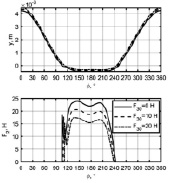
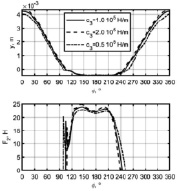
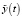, F1(t), F2(t) и F3(t). В качестве примера на рис. 4 представлены графики зависимостей yy(φ) и F2(φ), φ = ωt, полученные при изменении угловой скорости ω, а также F30 и c3. Так как начальные условия (8) записаны для установочного положения (при t = 0 Δ = 0), то для получения установившегося движения анализировалось N = 10 последовательных циклов изменения угловой координаты 
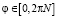. На графиках (рис. 4) показаны зависимости, соответствующие последнему циклу.
а) б)
в)
Рис. 4. Зависимости y(ω), F2(ω)
Как видно из представленных графиков в период сварки при y < 0 сила F2 > 0, причем в начальный момент при внедрении «пуансона» в материалы наблюдается скачок силы F2, что связано с ударом «пуансона» о материалы. При малых ω (ω = 100 c-1, рис. 4, а) усилие прижима «пуансоном» материалов в период сваривания остается практически постоянным,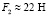 
. С ростом ω увеличиваются как пиковые значения силы F2, так и амплитуды ее колебаний. Увеличение усилия предварительного поджатия пружины 11 (рис. 1) приводит (рис. 4, б) к снижению силы F2 в период сварки, причем длительность контакта «пуансона» с материалами также уменьшается. Изменение коэффициента с3 (рис. 4, в) оказывает влияние на длительность контакта «пуансона» с материалами.
Заключение
В результате проведенного исследования разработано математическое, алгоритмическое и программное обеспечение для исследования динамики механизма привода пуансона машин ультразвуковой сварки с последовательным прерывистым выполнением шва. Полученные результаты позволяют анализировать колебания пуансона в процессе сварки при учете заданного кинематического внешнего воздействия со стороны исполнительного механизма, неудерживающего характера связи пуансона с материалами и других конструктивных параметров привода. Полученная математическая модель и разработанное программное обеспечение могут быть использованы для определения рациональных режимов работы и совершенствования оборудования ультразвуковой сварки материалов в швейной промышленности.