Рост сотовых технологий во всем мире последние годы происходит высокими темпами. В настоящее время около 5 млрд человек получают услуги беспроводной связи. Развитие сетевых технологий обычно делится на несколько поколений. Основной причиной этого роста является недорогая вычислительная мощность, которая приводит к доступным адаптерам беспроводной локальной сети WLAN (Wireless Local Area Network) и точкам доступа. Технологии и алгоритмы, используемые в различных поколениях сетей WLAN, также способствовали постепенному улучшению их производительности. Беспроводная локальная сеть (WLAN) в настоящее время является одной из наиболее востребованных технологий для беспроводного широкополосного доступа. Значительное повышение интереса к моделям систем поллинга обусловлено быстрым развитием широкополосных беспроводных сетей передачи данных. Был представлен анализ модели циклической (опросной) системы, адекватно описывающей широкополосные беспроводные сети WiFi и WiMax [1]. Более интересным с точки зрения приложений является случай, когда сервер не опрашивает непрерывно очереди, а уходит на отдых, когда очереди имеют недостаточное для обслуживания число заявок, и рассмотрим основную систему полинга с исчерпывающим обслуживанием, но в предположении, что время обслуживания в очередях распределено экспоненциально. Данная статья посвящена разработке математической модели и исследования эффективного управления широкополосными беспроводными сетями [2]. Пример отработки модели имитационной модели системы подключения к сети Wi-Fi при экспоненциальном законе распределения обеих очередей и равномерном законе распределения заявок в законе распределения появления абонентов представлены экспериментами на основе аналитической работы.
Описание математической модели
Модель – циклическая система поллинга [3, 4], которая имеет один сервер и N очередей (N ≥ 2), неограниченное место ожидания. В этом с параметром λi, 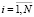 – поток заявок в i-ю очередь является простейшим потоком, интенсивность поступления заявок очередей должна быть выше порогового значения (ki для i-й очереди), ki ≥ 0,
– поток заявок в i-ю очередь является простейшим потоком, интенсивность поступления заявок очередей должна быть выше порогового значения (ki для i-й очереди), ki ≥ 0, 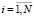 , очередь будет обслуживаться. До обслуживания i-й очереди для сервера является необходимым экспоненциально распределенное (параметр si), случайное время на разогрев. Когда в i-й очереди, время обслуживания заявок [5, 6] (параметр μi,
, очередь будет обслуживаться. До обслуживания i-й очереди для сервера является необходимым экспоненциально распределенное (параметр si), случайное время на разогрев. Когда в i-й очереди, время обслуживания заявок [5, 6] (параметр μi, 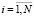 ) подчиняется экспоненциальному распределению. Пусть система функционирует в стационарном режиме и исследуем ее поведение в произвольный момент времени [1]. Вообще говоря, случайный процесс
) подчиняется экспоненциальному распределению. Пусть система функционирует в стационарном режиме и исследуем ее поведение в произвольный момент времени [1]. Вообще говоря, случайный процесс 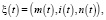 t ≥ 0, и m(t) = 0 в момент t, простое сервера и все еще в момент t, что: m(t) = 1 при сервер подключается, m(t) = 2 при сервер занимается обслуживанием, t ≥ 0; i(t) – является номером очереди, которые сервер может обработать за это время t, i(t) = 0 с текущим сервером не работает;
t ≥ 0, и m(t) = 0 в момент t, простое сервера и все еще в момент t, что: m(t) = 1 при сервер подключается, m(t) = 2 при сервер занимается обслуживанием, t ≥ 0; i(t) – является номером очереди, которые сервер может обработать за это время t, i(t) = 0 с текущим сервером не работает; 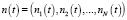 , nj(t) – является количеством заявок в j-й очереди в момент времени
, nj(t) – является количеством заявок в j-й очереди в момент времени 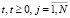 . Случайный процесс
. Случайный процесс 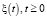 относится к марковским. При условии
относится к марковским. При условии 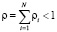 является загрузкой системы поллинга, где
является загрузкой системы поллинга, где 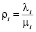 ,
, 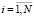 является загрузкой i-й очереди, и ρ < 1 является выполненным, вероятности процесса ξ(t), t ≥ 0:
является загрузкой i-й очереди, и ρ < 1 является выполненным, вероятности процесса ξ(t), t ≥ 0:
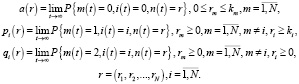
Тогда систему уравнений равновесия для стационарных вероятностей можно записать в соответствии со следующими формулами:
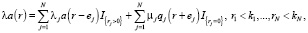 (1)
(1)
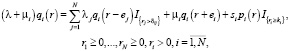 (2)
(2)
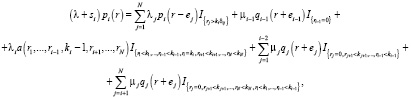
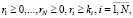 (3)
(3)
где 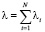 , ej является вектором строкой, элементы которой принимают значение «ноль» кроме j-го, принимающего значение «единица»,
, ej является вектором строкой, элементы которой принимают значение «ноль» кроме j-го, принимающего значение «единица», 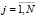 ;
; 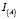 равен 1 в случае выполнения условия A, иначе
равен 1 в случае выполнения условия A, иначе 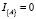 , δij является символом Кронекера,
, δij является символом Кронекера, 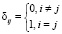 . Тогда получите
. Тогда получите
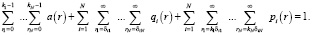
Необходимо ввести производящие функции:
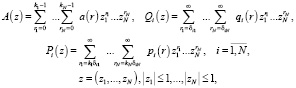
Выполнив умножение выражений и расчеты, отсюда получите
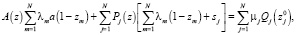 (4)
(4)
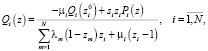 (5)
(5)
где 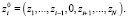
Так как производящая функция Qi(z) в области 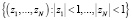 является аналитичной. Отсюда
является аналитичной. Отсюда
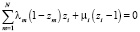 при
при 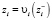 ,
,
где
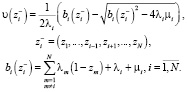
При этом 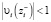 .
.
Числитель правой части (5) также должен принимать нулевое значение в точке 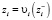 и
и
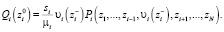
Если принять за Ri количество мест для ожидания в i-й очереди, 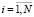 , то систему уравнений (1), (2), (3) для стационарных вероятностей состояний системы можно записать следующим образом:
, то систему уравнений (1), (2), (3) для стационарных вероятностей состояний системы можно записать следующим образом:
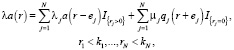 (6)
(6)
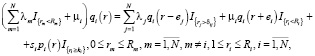 (7)
(7)
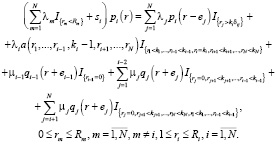 (8)
(8)
Выполнив замену одного из уравнений системы (6)–(8) на условие нормировки для стационарных вероятностей:
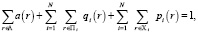
где 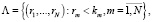
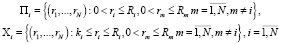 ,
,
можно получить систему уравнений относительно 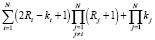 неизвестных. После этого:
неизвестных. После этого:
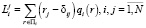 ;
; 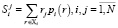 ;
;
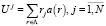 ;
; 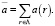
В котором: 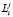 ,
, 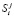 , U j по порядку, средняя длина j-й очереди в момент: обслуживания i-й очереди, подключения к i-й очереди, когда сервер простаивает и
, U j по порядку, средняя длина j-й очереди в момент: обслуживания i-й очереди, подключения к i-й очереди, когда сервер простаивает и 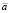 – средней доли простоя сервера в единицу времени сервера.
– средней доли простоя сервера в единицу времени сервера.
Вероятность 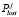 потери заявки, которая поступает в j-ю очередь, представляет из себя вероятность отсутствия в j-й очереди мест для ожидания в произвольный момент времени (количество заявок в ней составляет Rj):
потери заявки, которая поступает в j-ю очередь, представляет из себя вероятность отсутствия в j-й очереди мест для ожидания в произвольный момент времени (количество заявок в ней составляет Rj):
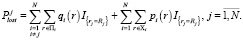
Исследование имитационного моделирования системы подключения к сети Wi-Fi
На основании вышеизложенной математической модели была разработана имитационная модель системы подключения к сети Wi-Fi в среде Microsoft Visual Studio 2015 на языке С# [7]. Входными данными для модели являются:
1. Закон распределения появления абонентов (равномерный или экспоненциальный).
2. Интенсивность появления абонентов (случайная величина).
3. Время, необходимое для подключения абонента (случайная величина).
4. Число каналов (буферов).
5. Пороговое значение очереди.
6. Максимальное значение очереди.
7. Количество пользователей.
Результаты моделирования
При запуске программы на экране появляется главное окно программы, выбор пункта «Настройки моделирования», и пример настроек модели представлен на рис. 1. Минимальное значение равно единице и соответствует режиму реального времени [7]. Необходимо установить: максимальное значение составляет 1000. Введенные значения будут определять количество секунд для моделирования модели, каждое входное значение будет соответствовать количеству секунд реального времени.
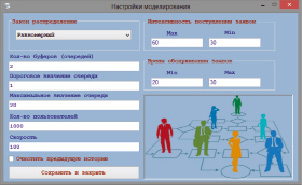
Рис. 1. Настройки моделирования
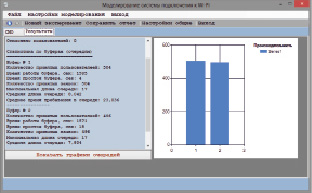
Рис. 2. Результаты моделирования, на графике показано количество принятых заявок
Ввода входных параметров в настройки моделирования, затем нажмите кнопку «Сохранить и закрыть» и попросить нажать кнопку «СТАРТ», после чего запускается процесс моделирования. Результаты и графики работы модели приведены на рис. 2.
Пример отработки модели имитационной модели системы подключения к сети Wi-Fi при экспоненциальном законе распределения обеих очередей и равномерном законе распределения заявок в законе распределения появления абонентов представлены экспериментами. Предположим, что входные параметры не меняются, меняется только «Интенсивность поступления заявок», его результаты в таблице.
Результаты имитационного моделирования системы подключения к сети Wi-Fi
|
Выходной параметр (Результаты моделирования) |
ЭКСПЕРИМЕНТЫ |
||||||||
|
1 |
2 |
3 |
4 |
||||||
|
λmax=60 |
λmin=10 |
λmax=55 |
λmin=20 |
λmax=50 |
λmin=30 |
λmax=40 |
λmin=15 |
||
|
Количество буферов (очередей) |
|||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
||
|
Количество принятых пользователеей |
574 |
426 |
511 |
490 |
508 |
492 |
541 |
459 |
|
|
Время работы буфера, с |
4147 |
4002 |
2172 |
2120 |
1616 |
1575 |
2832 |
2762 |
|
|
Время простоя буфера, с |
119 |
264 |
19 |
71 |
8 |
49 |
65 |
135 |
|
|
Количество принятых заявок |
574 |
426 |
511 |
490 |
508 |
492 |
541 |
459 |
|
|
Максимальная длина очереди |
5 |
4 |
8 |
7 |
10 |
9 |
7 |
6 |
|
|
Средняя длина очереди |
2,343 |
2,014 |
3,691 |
3,429 |
4,628 |
4,407 |
2,943 |
2,717 |
|
|
Среднее время пребывания в очереди |
12,343 |
11,371 |
13,282 |
11,753 |
13,154 |
11,665 |
12,305 |
11,416 |
|
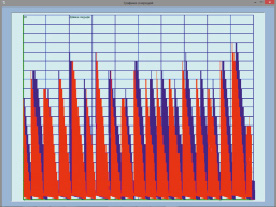
Рис. 3. На графике показана длина двух очередей
Численные эксперименты показывают, что графические результаты моделирования (а именно длин очередей в соответствии с появлением пользователей) приведены на рис. 3 (синим цветом показано изменение очереди первого буфера, красным – второго).
Выводы
Построены имитационные моделирования системы подключения к сети Wi-Fi на основе имитационных систем массового обслуживания с двумя очередями. Графические результаты моделирования, а именно длин очередей в соответствии с появлением пользователей.
Данная работа посвящена разработке математических моделей для исследования эффективного администрирования широкополосных беспроводных сетей.



