В исследованиях для метеопрогнозов обычно используют базу данных о погоде за 12 месяцев и их совокупность называют «тестовый базовый год» (TRY) или типичный метеогод (TMY). TMY – набор данных с почасовыми значениями метеорологических элементов. Выбор таких типовых погодных условий для заданных локализаций важен в моделировании с прогнозом погоды, тепловых характеристик зданий, сооружений и т.д., что в итоге даёт проектантам возможность наблюдать продолжительные периоды исследуемых данных или же отбирать искомый, типичный год из временной последовательности TMY. Данные численного прогнозирования погоды (ЧПП) представляют собой форму данных модели погоды. ЧПП фокусируется на проведении текущих наблюдений за погодой и обработке этих данных с помощью компьютерных моделей для прогнозирования будущего состояния погоды. Знание текущего состояния погоды так же важно, как и числовые компьютерные модели, обрабатывающие данные.
Цель исследования: изучение возможностей сезонной модели авторегрессионного интегрированного скользящего среднего для прогнозирования погоды и выявления тенденций в изменении климата в регионе на базе кода Python 3.6 (Miniconda).
Материалы и методы исследования
Одной из наиболее популярных и часто используемых моделей временных рядов является модель авторегрессионного интегрированного скользящего среднего (ARIMA) [1–3]. Основное предположение, сделанное для реализации этой модели, состоит в том, что рассматриваемый временной ряд является линейным и следует определенному известному статистическому распределению, такому как нормальное распределение. Модель ARIMA имеет подклассы других моделей, таких как модели авторегрессии (AR) [3], скользящего среднего (MA) [4] и авторегрессии скользящего среднего (ARMA) [5]. Для сезонного прогнозирования временных рядов Бокса и Дженкинса (БД) [6] предложили довольно удачный вариант модели ARIMA, а именно, сезонного его варианта – SARIMA [7]. Но серьезным ограничением этих моделей является предполагаемая линейная форма связанных временных рядов, которая становится неадекватной в некоторых практических ситуациях, для этого некоторые авторы предложили различные нелинейные стохастические модели [7], однако с точки зрения реализации они не так просты и удобны, как модели ARIMA. Обзор литературы показывает, что не существует единой модели, которая бы последовательно превосходила другие модели во всех ситуациях; поэтому в данной статье предпринята попытка сравнить подходы, чтобы найти лучший метод, который можно использовать для прогнозирования погоды в Калмыкии.
В статье используются данные о ежемесячных метеоданных на стации г. Элиста № 1 с 1966 г. по 2017 г. и станции № 2 в 1927–2017 гг. Для сбора информации используются значения временных рядов из открытых источников: лаборатории автоматизированной информационной системы Росгидромета и NOAA.
Метеостанция Элиста:
– Синоптический индекс: 34861, Высота над уровнем моря: 133 м;
– Географическая широта: 46.315488, долгота: 44.279401 °.
nms=['S_IS',1,2,3,'YE_I','MO_I','DA_I','SR','PN','NV','SV','TV','DP','OV','VV','AD','KO','SO','GD','TP','ADR']
test = pd.read_table(r''…\Inp\sr77.csv'', sep=';' , engine='python', error_bad_lines= False, parse_dates= {'Datetime':[1,2,3]}, names=nms, header= None ); test_original = test.copy()
Вначале была выполнена частичная индексация и нарезка строк, выборка временных рядов, разделение и повторная выборка за разные месяцы с различными агрегатами.
Методология и выбор модели. Модели ARIMA зависят от теории статистического моделирования, известной как метод Бокса – Дженкинса. Была использована структура с месячными данными в сезонном формате, модель при этом имеет следующую нотацию ARIMA (p, d, q), (P, D, Q)S , где (p, d, q) – несезонная часть и, соответственно, (P, D, Q) является сезонной частью модели. Модель требует диагностической проверки до прогнозирования, путем проверки нормальности остатков или с помощью графика квантиль-квантиль (Q-Q). Проверка адекватности модели обеспечивается статистикой Люнга – Бокса Q. Тестовая статистика Q задается как
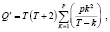
где pk – автокорреляция образца при запаздывании k.
Создание модели ARIMA состоит из четырех систематических этапов (идентификация, оценка, диагностическая проверка и применение или прогноз). Были изучены и установлены компоненты серии для удаления методом stl – сезонной и трендовой декомпозицией с использованием метода LOESS (''STL)
Стационарность изучалась на базе графиков adf.test(), ACF, PACF.
data[''TV''].plot(figsize=(15, 5))
Результаты исследования и их обсуждение
Для анализа данных об осадках для построения прогнозной модели использовался подход Бокса – Дженкинса. Модель ARIMA предназначена для несезонных нестационарных данных, а авторы этого подхода обобщили модель для учета сезонности и назвали SARIMA. В этой модели сезонная дифференциация соответствующего порядка используется для удаления нестационарности из ряда. Сезонная разница первого порядка представляет собой разницу между наблюдением и соответствующим наблюдением предыдущего года и рассчитывается как zt = yt – yt-s (модель SARIMA (p, d, q)×(P, D, Q)S).
Для автокорреляции и выбора порядка прогнозирования на базе моделей скользящего среднего (МСС) рассматривается как процесс прогноза на тот период, который следует непосредственно за периодом искомых наблюдений. МСС обычно используются для сглаживания краткосрочных колебаний в данных временных рядах и выделения долгосрочных трендов.
unsmoothed = df['Temperature'][ 2019-Jul -01':'2019-Jul -15'] # извлечения данных о температуре
# создания нового DataFrame с временными рядами, сглаженными и не сглаженными в виде столбцов: July
July = pd.DataFrame({'smoothed':smoothed, 'unsmoothed':unsmoothed})
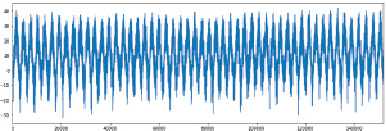
Рис. 1. Температурный график 1967–2017 гг. в г. Элиста
Обнаружены необратимые параметры начального сезонного скользящего среднего с установленным значением true для параметра обратимости для empce.
Параметры aic
0 (2, 3, 1, 0) 3888.642174
1 (2, 3, 1, 1) 3888.642174
2 (3, 2, 1, 1) 3888.763568
3 (3, 2, 1, 0) 3888.763568
plotMovingAverage(ads, 7, plot_intervals=True)
Ежедневное сглаживание почасовых данных прогноза температуры для июня 2019 г. Ниже показаны доверительные интервалы для сглаженных значений.
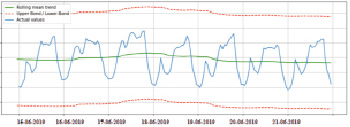
Рис. 2. Скользящее среднее с окном =7
При вызове функции fit можно передать максимальное количество лагов и критерий вызова:
results = model .fit (maxlags = 15, ic = 'aic')
На графике вертикальная ось представлена следующими уравнениями:
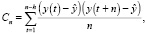
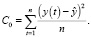
Горизонтальная ось представляет временную задержку (предыдущие временные шаги) h
from pandas.plotting import ac_plot
pd.plotting. ac_plot(df['TV'].mean)
pd.plotting.lag_plot(df[df['TV'].mean])
Для разложения временных рядов, определения тенденции и шума необходимо разложить сезонную составляющую вышеперечисленных временных рядов. Для определения подходящей модели строится график ACF временного ряда.
data.pivot_table(['SV','TV','AD'],['YM'], aggfunc='mean').head(200) #сводная таблица, подсчет по группам
Данные в табл. 1 явно показывают тренд на увеличение температуры на 1,1 °С за последние 50 лет, если же взять статистику за десятилетие (наблюдение ведётся с 1927 г.) с 01.01.1928 г. по 31.12.1937 г. и с 01.01.1998 г. по 31.12.2017 г., то разница ещё разительнее – 1,79.
Таблица 1
Средние значения по атм. давлению (AD), силе ветра (SV) и температуре воздуха (TV)
|
№ год |
1970 |
1980 |
1990 |
2000 |
2010 |
||||||||||
|
AD |
SV |
TV |
AD |
SV |
TV |
AD |
SV |
TV |
AD |
SV |
TV |
AD |
SV |
TV |
|
|
0 |
995,9 |
6,1 |
9,6 |
998,3 |
5,8 |
8,6 |
998,9 |
5,7 |
10,5 |
998,8 |
5,6 |
10,5 |
997 |
4,9 |
11,5 |
|
1 |
998,9 |
7,2 |
10,0 |
997,8 |
5,3 |
10,5 |
999,6 |
5,5 |
9,8 |
997,9 |
5,5 |
10,7 |
993,8 |
4,6 |
9,3 |
|
2 |
1001,4 |
6,5 |
9,2 |
999,1 |
5,1 |
8,9 |
998,8 |
6,0 |
9,1 |
998,3 |
5,3 |
10,1 |
993,3 |
4,7 |
10,2 |
|
3 |
999,4 |
6,0 |
8,8 |
997,7 |
5,5 |
10,5 |
1000,2 |
7,2 |
7,9 |
999,4 |
5,0 |
9,5 |
992,3 |
4,4 |
10,9 |
|
4 |
1000,5 |
5,7 |
9,2 |
1000,9 |
6,4 |
9,1 |
999,5 |
6,8 |
9,1 |
997,9 |
5,2 |
10,6 |
994,4 |
5,0 |
10,2 |
|
5 |
999,4 |
6,0 |
10,6 |
998,5 |
6,1 |
8,5 |
998,1 |
7,5 |
11,0 |
999,1 |
5,1 |
10,7 |
994,2 |
4,9 |
11,0 |
|
6 |
1000 |
6,2 |
8,2 |
1000 |
5,7 |
9,6 |
1000,5 |
7,3 |
9,0 |
998,0 |
4,9 |
10,3 |
993,5 |
4,4 |
10,3 |
|
7 |
999,9 |
5,6 |
8,9 |
999,8 |
5,6 |
7,3 |
997,7 |
6,5 |
9,2 |
998,1 |
4,8 |
11,8 |
993,9 |
4,5 |
10,6 |
|
8 |
998,8 |
5,7 |
8,7 |
998,3 |
5,1 |
9,0 |
999,0 |
6,6 |
10,1 |
999,1 |
4,5 |
10,4 |
|||
|
9 |
999,0 |
6,6 |
10,4 |
998,6 |
5,7 |
10,5 |
998,2 |
5,9 |
11,1 |
997,6 |
4,5 |
10,8 |
|||
|
Ср |
999,3 |
6,2 |
9,4 |
998,9 |
5,6 |
9,3 |
999,1 |
6,5 |
9,7 |
998,4 |
5,0 |
10,5 |
994,1 |
4,7 |
10,5 |
df[data['dates'] <='1991-01-01']['OV'].mean() #средние показатели влажности для Республики Калмыкия – 68.882, c '1991-01-01 = 71.388, (соответственно, для средних температур: 9.363 и 10.211).
Средние температуры, зарегистрированные с января 1966 г. по декабрь 2017 г., представлены на рис. 3. Из рисунка видно, что температурный ряд не имеет трендовой картины, и поэтому его можно назвать стационарным, однако есть периодические всплески.
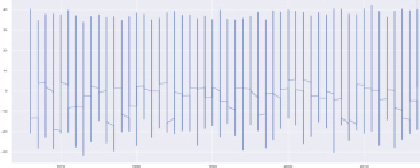
Рис. 3. График временных рядов средней температуры, записанной с 1967 по 2017 г.
Для определения, являются ли остатки белым шумом и типа распределения, необходимо построить нормальный график вероятности остатков, при этом информационный критерий Акаике (AIC) и байесовский критерий Шварца (SBC) используются для критериев выбора самой модели.
Сезонная авторегрессионная интегрированная скользящая средняя с экзогенными регрессорами (SARIMAX) относится к основным классам оценки, которые могут быть доступны через статмодели и их классы результатов.
# Имитация временного ряда…, построить модель
class ARe2(...MLEModel):
def __init__(sf, eog): # Инициализировать модель пространства состояний
# параметры модели …, параметры запуска и имена параметров
def start1(sf): …
mod = ARe2(eog) # Создать и подобрать модель
xres = mod.fit()
Вывод информации по получившейся модели в табл. 2.
set the parameters that give the lowest AIC
p, q, P, Q = result_table.parameters[0]
Таблица 2
Результаты модели SARIMA (2,1,3)x (1,1,0)24
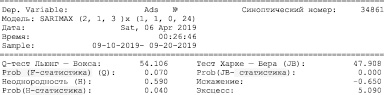
Объект результатов имеет множество атрибутов и методов, которые можно ожидать от других результатов Statsmodels, включая стандартные ошибки, z-статистику и прогнозирование. Возможно расширенное использование, включая указание преобразований параметров и указание имен для параметров для более информативного вывода результатов. Можно сделать прогноз и прогнозирование после оценки, при этом конечный период может быть указан как дата – тип.
pred = res.get_predion()#Выполнить прогнозирование
fore = res.get_fore('2019')
fig, ax = plt.subplots(figsize=(10,4))
df['lff'].plot(ax=ax, style='k.', label='наблюдения') # Отобразить график
pred.preded_mean.plot(ax=ax, label=' прогноз')
pred_ci = pred.conf_int(alpha=0.05); pred_ind = np.arange(len(pred_ci))
ax.fill_between(pred_ind[2:], pred_ci.iloc[2:, 0], pred_ci.iloc[2:, 1], alpha=0.1)
fore.preded_mean.plot(ax=ax, style='r', label='Прогноз')
fore_ci = fore.conf_int();fore_ind = np.arange(len(pred_ci), len(pred_ci) + len(fore_ci))
ax.fill_between(fore_ind, fore_ci.iloc[:, 0], fore_ci.iloc[:, 1], alpha=0.1)
ax.set_ylim((4, 8)); # Очистка графика
Поэтому для улучшения отдачи в исследовании необходимо с большой тщательностью отнестись к первоначальному выбору задержки и к поиску баланса между оптимальным качеством прогнозирования и длиной горизонта прогнозирования.
plotHoltWinters(ads.Ads, plot_intervals=True, plot_anomalies=True)
Из графика на рис. 4 следует, что модель смогла успешно аппроксимировать начальные временные ряды, фиксируя ежедневную сезонность, общую тенденцию к снижению и даже некоторые аномалии. На отклонениях модели можно зафиксировать, что модель довольно резко реагирует на изменения в структуре ряда, но затем быстро возвращает отклонение к нормальным значениям. Эта особенность модели позволяет быстро создавать системы обнаружения аномалий, даже для шумных данных, не тратя на подготовку данных и обучение модели.
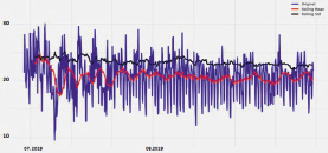
Рис. 4. Скользящее среднее и стандартное отклонение
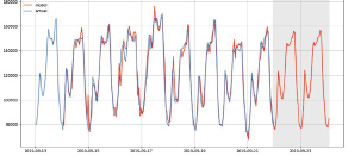
Рис. 5. Средняя абсолютная ошибка в процентах (4,46 %)
plotHoltWinters(currency.TV)
Анализ остатков модели представляет собой важный тест модели. Процедура оценки предполагает, что остаток не автокоррелирован и что он нормально распределен. Ниже остаточный компонент этой модели:
tsplot(best_model.resid[24+1:], lags=60)
Очевидно, что остаток является сглаженным и, соответственно, нет явной автокорреляции. Дальше используется эта функция для модели для прогнозирования:
def plotSARIMA(series, model, n_steps):
Параметры модели из табл. 2 являются значимыми. Графики невязок на рис. 6 показывают, что распределение остатков предложенной модели является гауссовским (белый шум). Это хорошо видно на рисунке ниже. Следовательно, предложенная модель оправдана, так как хорошо вписывается в тестовые данные. За исключением некоторых незначительных всплесков, которые лежат за пределами 95 % доверительного интервала, все остальные точки находятся в пределах доверительного интервала. Прогнозируемые цифры, как правило, достаточно близки к фактическим точкам. Модель выполняет свою предсказательную функцию.
При вычитании скользящих средние из исходных наблюдений получаются конкретные сезонные значения, то, что остается в конкретных сезонных колебаниях, обычно представляет собой стационарный горизонтальный ряд с двумя эффектами, которые приводят к тому, что конкретные сезонные колебания отклоняются от абсолютно прямой линии: сезонные эффекты и случайная ошибка в исходных наблюдениях. На рис. 5 показаны результаты.
plotSARIMA(ads, best_model, 50)
В итоге были получены адекватные прогнозы. Данная модель ошиблась в среднем на 4,46 %, что в целом неплохо. Однако общие затраты на подготовку данных, нахождение ряда в стационарном режиме и выбор параметров могут не стоить такой точности.
Во время начального выбора параметров задержки необходимо найти баланс между оптимальным качеством прогнозирования и длиной горизонта прогнозирования.
plotModelResults(lr, plot_intervals=True)
plotCoefficients(lr)
lasso = LassoCV(cv=tscv)
lasso.fit(X_train_scaled, y_train)
…
# Прогнозирование Временных Рядов: Модель Скользящего Среднего
plt.figure(figsize = (15,8))
model = ARIMA(Train_log, order = (0,1,2)) # here the p value is 0 since it is moving average model
…
fit1 = sm.tsa.statespace.SARIMAX(Train.Count, order = (2,1,3), seasonal_order =(0,1,0,24)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start=''2019-9-1'', end=''2019-9-25'', dynamic=True)
plt.figure(figsize=(16,8))
plt.plot(Train['Count'], label = ''Train''); plt.plot(valid.Count, label = ''Validation'');
plt.plot(y_hat_avg['SARIMA'], label =''SARIMA'')
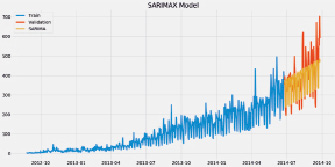
Рис. 6. Прогноз SARIMA (2,1,3)x (1,1,0)24
Прогноз показан красной линией и точками по сравнению с тестовым набором данных с января 1967 г. по декабрь 2017 г. синей линией. 95 % доверительный интервал перекрыт желтыми линиями. Прогнозная модель SARIMA является ценным инструментом, обладающим потенциалом для раннего предупреждения, выявления изменений погоды и может предоставить надежную информацию для проактивной работы, поскольку значения прогноза из модели SARIMA(2, 1, 3)x(1, 1, 0)24, наиболее подходящей для данной модели, значениям прогноза.
Заключение
Установлено, что совокупность данных средних температур в г. Элисте с 1966 по 2017 г. является стационарной, что подтверждено автокорреляционными, частичными автокорреляционными эпюрами и проведением теста Дики Фуллера. Для исключения сезонной составляющей во временных рядах средних температур необходимо было провести одно сезонное дифференцирование. Модели-кандидаты были разработаны, как указано в процессе построения модели, в соответствии с подходом Джекинса, и значения AIC были получены для каждой модели-кандидата. Окончательная модель была выбрана SARIMA(2, 1, 3)x(1, 1, 0)24.
В итоге были получены адекватные прогнозы. Ошибка модели – 4,46 % в среднем, что неплохо для прогноза погоды. Обычно вероятностный прогноз предоставляет для исследователя больше необходимой информации для принятия экономических решений, чем стандартные точечные прогнозы.
Остатки проверены, было обнаружено, что они следуют за белым шумом, что означает, что они были не коррелированы. Остатки также прошли тест на нормальность (график Q-Q). Проведена диагностика модели, которая указывает, что модель может использоваться для прогнозирования. Значения прогноза не выходят из 95 % доверительного интервала, что дает возможность рассматривать его как интервал значений θ параметра, совместимых с искомыми опытными данными и не противоречащих им в этих диапазонах. Дальнейшие планы исследований будут направлены на проекты, связанные с индексом аридности (прогноза песчаных бурь) в республике Калмыкия на основе параметров интенсивности засухи Палмера и Де Мартонна.



