В процессе укрупнения производственных предприятий, а также при их взаимодействии с другими предприятиями в рамках реализации жизненного цикла изделий, в том числе при проектировании различных информационных систем [1], неизбежно возникает вопрос интеграции систем автоматизации в единое информационное пространство (ЕИП). Существуют проблемы при использовании программных средств различных вендоров, имеющих зачастую свои закрытые форматы при сохранении геометрических моделей (ГМ). ГМ – математическое описание структуры изделия или инфраструктуры, которое включает полный набор координат и геометрических характеристик его элементов (и других характеристик, являющихся параметрами) [2]. Интеграция программ с несовместимыми форматами может привести к дополнительным временным затратам по восстановлению параметров ГМ, а также при осуществлении информационной поддержки жизненного цикла изделия. Особенно важно это учитывать при передаче параметров ГМ между предприятиями, если они в процессе проектирования используют системы разных вендоров.
В состав систем автоматизации и разработки изделий входят системы автоматизированного проектирования (CAD-системы), системы управления данными об изделии (PDM-системы). От корректного взаимодействия таких систем, интеграции в общую структуру единого информационного пространства зависит в том числе конкурентоспособность предприятий [3, 4].
Отличительными особенностями функционирования систем автоматизации в рамках ЕИП становятся:
– широкое использование информационной модели (ИМ) изделия на этапах жизненного цикла (ЖЦ), ИМ включают геометрические модели (ГМ), содержащие атрибутивную информацию и топологию;
– высокая трудоемкость процесса передачи ГМ в среде разнородных автоматизированных систем в рамках предприятия и между предприятиями в случае использования разных вендоров, как отечественных, так и зарубежных;
– возможные потери параметров ГМ, что может негативным образом отразиться на временных показателях процесса разработки и эксплуатации изделий.
Основной проблемой на современном этапе информационной поддержки процессов жизненного цикла изделий является отсутствие единого подхода к обеспечению процессов интеграции разнородных автоматизированных систем. Неверно оцененные параметры результата передачи ГМ могут негативным образом сказаться на экономических показателях предприятия. Например, потери параметров ГМ на начальном этапе ЖЦ могут привести к сложностям (техническим, экономическим) на других стадиях при интеграции, так как последующая работа при выполнении другими предприятиями, в свою очередь, может привести к значительным потерям ресурсов на доработку либо даже к повторной разработке изделия. Возникает потребность в разработке расширенной модели передачи параметров геометрических моделей между CAD- и PDM-системами на основании сравнения близости графов и графовых структур.
Существуют универсальные нейтральные форматы для информационного обмена программных сред, например STEP, IGES и др. С помощью этих форматов отсутствует возможность передать все параметры ГМ из одной среды в другую, разное количество параметров передается между программными средами при разработке одного файла ГМ [5]. Необходимо провести оценку эффективности обработки данных при передаче параметров между средами в нейтральных форматах с применением метрик. Решение вышеперечисленных проблем и является целью настоящего исследования.
Методика сравнения близости графов и графовых структур изделий для оценки эффективности передачи ГМ
Модель передачи параметров геометрических моделей основана на метриках эффективности передачи ГМ. Метрика эффективности передачи ГМ рассчитывается с применением сравнения близости графов и графовых структур. В результате при реализации графа иерархической структуры параметров [6] получены структурные весовые коэффициенты показателей значимости параметров ГМ. Данная классификация содержит в себе параметры интеграции различных систем автоматизированного проектирования и систем управления данными об изделии, а также части атрибутивных параметров ГМ, что реализовано с применением фреймов [7]. ГМ представляется в виде графовой структуры, включающей в себя дерево изделия, не содержащее циклов (N-арное дерево), и фреймы, содержащие параметры ГМ.
На рис. 1 показаны составляющие иерархического пространства параметров ГМ.
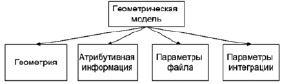
Рис. 1. Составляющие иерархического пространства параметров ГМ
В результате проведенных исследований в области интеграции CAD- и PDM-систем различных вендоров, на основании графа иерархической структуры параметров определен список параметров ГМ для метрик оценки передачи. Ниже представлен пример части списка параметров ГМ:
– параметры сборки;
– дерево создания;
– точность геометрии;
– сборочные зависимости;
– параметрические связи;
– параметры файла;
– физические параметры;
– функциональные параметры;
– идентификационные параметры;
– административные параметры; и др.
На первом этапе сравнивается близость только деревьев ГМ на основании математического представления деревьев в виде матриц смежности. Информация о параметрах ГМ отражается в наличии рёбер графа, а также в случае описания графов типа дерево ГМ, информация содержится в первую очередь в вершинах.
Матричное представление графов может применяться для выявления сходства структуры графов (сравнения деревьев). Один из вариантов сравнения основан на операции вычитания матриц. Чем меньше будет полученный результат в виде матрицы, тем более похожи графы. В формуле (1) представлен пример матриц смежности (рис. 2) исходной ГМ (А) и полученной ГМ в результате передачи (В), которые являются исходными данными для сравнения. Известно, ребро – это связь между вершинами, следовательно, при утрате вершины дерева теряется и ребро. Тогда требуется ввести дополнительные метрики, предложенные далее, если необходима более точная оценка.
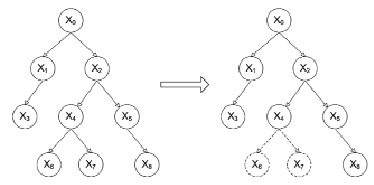
Рис. 2. Граф исходной ГМ (A) и утраченные элементы графа переданной ГМ (B)
A =  , B =
, B =  (1)
(1)
Метрика эффективности передачи ГМ на основании сравнения близости графов рассчитывается на основании выражения расстояния Хэмминга (с применением матриц смежности):
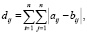 (2)
(2)
где а – параметры 1-й ГМ i-й строки и j-го столбца; b – параметры 2-й ГМ i-й строки и j-го столбца, полученной после передачи; n – количество элементов.
Существует альтернативный вариант расчета метрики, подразумевающий наличие общих параметров c для 1-й и 2-й ГМ на основании меры Сёренсена:
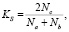 (3)
(3)
где Nа – количество параметров 1-й ГМ, Nb – количество параметров на 2-й ГМ в результате передачи, Nс – количество параметров, общих для 1-й и 2-й ГМ.
Результаты позволят визуально определить, какие именно параметры ГМ были потеряны в процессе интеграции. Результаты также могут быть экспортированы в добавочный текстовый файл к файлу ГМ.
Для повышения точности оценки передачи параметров ГМ требуется учитывать дополнительные параметры передачи каждого узла дерева ГМ, для этого применяется графовая структура [8] параметров передачи ГМ. На рис. 3 представлен пример графовой структуры некоторой ГМ, которая состоит из небольшого количества составляющих элементов.
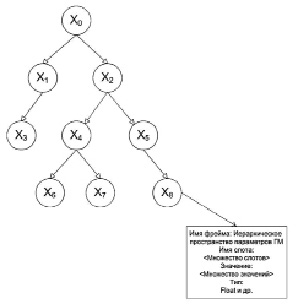
Рис. 3. Графовая структура ГМ
Графовая структура представляет дерево изделия и параметры каждого узла ГМ в виде фрейма, который содержит список параметров ГМ. Изделие сохраняется в нейтральный формат в виде файла. Нулевой уровень содержит список параметров для всего изделия, представленного в виде дерева, каждый узел следующего уровня содержит свой список параметров. Параметры реализованы в виде фреймового представления.
Близость графовых структур предлагается рассчитать на основании метрики Манхэттена – расстояние d1 между двумя векторами p, q в n-мерном вещественном векторном пространстве с заданной системой координат – сумма длин проекций отрезка между точками на оси координат:
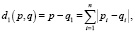 (4)
(4)
где p = (p1,p2,p3,…pn) и q = (q1,q2,q3,…qn) – векторы.
При рассмотрении графовых структур при передаче ГМ выделены случаи: параметры переданы полностью и сохранились; вершины переданы частично (или с ошибкой), частично сохранены; вершины не удалось передать, данные утеряны; а также существует возможность не получить результат вообще, т.е. нет данных о результатах передачи:
p = (p1, p2) – параметры исходной ГМ, q = (q1, q2) – параметры переданной ГМ,
где
p1 = q1; p2 = q2 – данные переданы корректно;
p1 = q1; p2 ≠ q2 – данные переданы частично или с ошибкой;
p1 = q1; p2, q2 =* – нет данных или данные могли быть утеряны полностью.
Выявлено, что данные при передаче бывают количественные и номинальные. Количественные данные можно сравнить с использованием метрики Манхэттена. Номинальные данные позволяют получить сведения о том, состоялся ли факт передачи данных между системами, произошла ли ошибка, либо значение отсутствует. Номинальные данные можно сравнить с помощью метрики Хэмминга.
При сравнении атрибутов (списков параметров) предполагается цикл обхода всех вершин и сравнение в каждой вершине списков атрибутов в исходной и переданной модели, также, если необходимо, возможно провести расчет с учетом весов вершин:
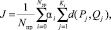 (5)
(5)
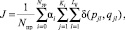 (6)
(6)
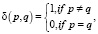 (7)
(7)
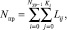 (8)
(8)
где αi – иерархические веса уровней параметров передачи;
d(P, Q) – функция сравнения параметров с учетом всех вершин некоторого уровня;
Nур – количество уровней;
Nпр – количество признаков;
Ki – сумма всех вершин i-го уровня;
Lij – сумма переданных признаков вершины;
δ(p, q) – индикаторная функция сравнения параметров.
Далее рассмотрен случай сравнения ГМ без учета различной значимости уровней. При этом иерархические веса уровней равны между собой:
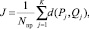 (9)
(9)
K – количество вершин.
Танимото предложил меру сходства, позволяющую определить степень схожести двух множеств. Данная мера известна как коэффициент Танимото. Количественные данные по передаче параметров можно также рассчитать при помощи данного коэффициента:
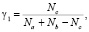 (10)
(10)
где Nc – число общих параметров у Na и Nb; в свою очередь, Na – множество параметров исходной ГМ; Nb – множество параметров полученной в результате передачи ГМ; соответственно a, b – параметры исходной и полученной в результате передачи ГМ; c – общие параметры для исходной и полученной в результате передачи ГМ.
Результаты исследования и их обсуждение
Проведено исследование близости ГМ с применением теории графов; структура ГМ и результаты передачи представлены в виде графа. В результате проведенного исследования сформирована структура графа в виде списка отдельных сборочных единиц, которые включили в себя следующие группы параметров: геометрия, атрибутивная информация, параметры файла, а также параметры интеграции.
Искажения для разных моделей не всегда линейно зависят от количества элементов, а скорее от систем и форматов. Поэтому требовалось выяснить, какие возможны потери при передаче в условиях мультивендорности. Тестовые проверки проводились для нейтральных форматов: STEP, IGES, JT. В результате проведения экспериментов по передаче параметров между различными системами автоматизированного проектирования и системами управления данными об изделии с помощью нейтрального формата STEP получалось значение метрик эффективности передачи ГМ на основании сравнения близости графов от 0,2 до 0,5 (диапазон от 0 до 1). При использовании систем автоматизации одного вендора значения метрик более низкие. При применении разных вендоров получается более высокий результат объема потерь при передаче параметров. Определено, что потери при передаче параметров ГМ будут более низкими при использовании формата STEP, чем IGES, JT.
Условия, при которых проводился расчет значений сравнения близости графовых структур ГМ:
– в рамках сборки (максимально для данного эксперимента – десятки элементов);
– на одном из уровней графа (структуры) узлов;
– на уровне параметров отдельного узла.
Выводы
Выявлено отсутствие обобщенной машинно-независимой модели передачи параметров геометрических моделей на основании сравнения близости графов и графовых структур между CAD- и PDM-системами. Модель выявляет потери при передаче параметров ГМ, что позволяет оценить затраты, необходимые на восстановление информации на основании метрик. Предложена расширенная модель структуры параметров ГМ в виде графовой структуры. Проведен анализ аспектов интеграции CAD- и PDM-систем. Исследованы методики оценки передачи ГМ между системами автоматизации на основании метрик. Предложен метод расчета метрики оценки потерь при передаче данных между CAD- и PDM-системами.



