Высшее учебное заведение должно готовить студентов не только к деятельности специалистов в определенной области, но и к продуктивной деятельности в своей личной и общественной жизни. Компетентный выпускник – личность, которая достигает поставленной перед собой цели, делает правильный и осознанный выбор пути решения проблем, возникающих в личностной и профессиональной жизни, отвечающий за свои решения и поступки, мирно живущий в поликультурном мире и др. Каждое из приведённых качеств входит в определение понятия «компетентность».
С другой стороны, в государственном образовательном стандарте школьного общего образования последнего поколения, а также в новом предметном стандарте по математике в общеобразовательных школах Кыргызской Республики в качестве приоритетных направлений обозначен компетентностный подход, это подразумевает способность ученика самостоятельно применить полученные математические знания как в учебной и трудовой деятельности, так и в личной. В связи с этим в предметном стандарте пересмотрены подходы ко многим вопросам, в частности в определении содержательных линий, усилен прикладной аспект математики, выборе методов и приемов, форм организации обучения, ресурсов, к системе оценивания и др.
В данной работе определено понятие «компетентностного подхода», «компетенции»; в контексте компетентностного подхода обоснованы и разработаны методические пути обучения математическому анализу студентов вузов педагогического направления, построена техника формирования компетенции; на основе опыта практической деятельности обучения математическому анализу разработаны и систематизированы по группам А, В, С компетентностно-ориентированные задания.
Безусловно, из этого следует, что будущий учитель математики в своей будущей педагогической деятельности должен направлять свою работу на формирование у своих учеников не только предметных компетентностей, но и ключевых. Школа должна выпускать компетентного ученика, т.е. ученика готового продолжить свое образование, найти свое место в жизни, успешно проявить себя в обществе.
А также отметим, что на сегодняшний день остается актуальным вопрос улучшения обучения дисциплины математического анализа в вузах педагогического направления. Известно, что должна быть преемственность полученных школьных математических знаний и вузовских, другими словами, полученные в школе знания и умения должны помогать при обучении высшей математике, в том числе математическому анализу. Но как показывает практика, для успешного последующего изучения математического анализа уровень знаний и умений выпускников школ зависит от требований стандарта. Поэтому необходимы эффективные подходы в обучении математическому анализу в вузе, для наверстывания, упущенного и в то же время не отставания от программы.
Объективная потребность в качественной подготовке студентов с учетом реалии современности, способного решать проблемы, возникающие в реальных жизненных ситуациях и профессинальной деятельности, а также необходимость в разработке эффективных методических основ обучения дисциплине «математический анализ» определили исследование проблемы формирования профессиональной и ключевой компетентности у студентов в процессе обучения математическому анализу.
Цель исследования: обоснование и разработка эффективных путей обучения математическому анализу в вузе педагогического направления.
Предмет исследования: методическая подготовка будущих учителей математики в вузах педагогической направленности к компетентностному обучению математике старшей ступенях общего образования.
Материалы и методы исследования
Образованным человеком является тот человек, который при вхождении в разные социальные общности строит собственное продуктивное действие. Следует отметить, что именно для достижения практических результатов и реализации продуктивных действий применяется компетентностный подход.
Компетентностным подходом в образовании является преимущественная ориентация на его результаты: формирование профессиональных и общекультурных компетенций, социализацию, самоопределение, индивидуальность и самоактуализацию. Именно такой подход дает направление системе образования на обеспечение качественной подготовки на основании потребностей общества, и это согласуется не только с потребностью вливания в общественную деятельность, но и потребностью общества использовать возможности личности [1].
А.К. Наркозиев исследовал теоретические основы компетентностного подхода программ образования в условии кредитной технологии [2].
Концепция компетентностного подхода в образовании исследовалась в работах В.И. Байденко, И.А. Зимней, Л.И. Коновалова, Б.А. Сазонова, В.С. Сенашенко, Ю.Г. Татур, О.Б. Томилина, А.В. Хуторского.
Вышеназванные исследователи отметили, что компетентный специалист успешно может применить в своей практике свои знания, умения и навыки. По результатам проведённых исследований установлено, что имеются различные взгляды на компетеностный подход.
Исследователь Е.Я. Коган считает, что это совершенно новый подход, который требует изменить отношения к позиции учителя, к образованию учащихся; и этот подход должен привести к глобальным изменениям, от изменения сознания до изменения методической базы [3].
В контексте данного исследования обратимся и к понятию компетенция, которая является основным понятием при компетентностном подходе в обучении студентов.
Компетенция – это нечто большее, чем просто знания или навыки; она подразумевает способность специалиста отвечать комплексным требованиям за счет мобилизации и использования своих психологических ресурсов (включая навыки и ценности) в конкретных обстоятельствах.
Компетенция имеет следующие характеристики:
1. Компетенция – это динамичное сочетание знаний, умений и навыков, которые необходимы для приобретения компетенции.
2. Компетенция связана со всеми тремя направлениями, позволяющими оценить деятельность специалиста: знания, умения и навыки.
3. Компетенции связаны с деятельностью специалиста, и поэтому они поддаются наблюдению и их можно продемонстрировать.
4. Так как компетенции поддаются наблюдению, их можно измерить.
5. Их также можно передать.
Для внедрения компетентностного подхода в процесс обучения необходимо несколько этапов. Так, на первом этапе можно формировать элементарные общие учебные компетенции студентов, такие как:
– выявление ключевых моментов, т.е. основы лекционного материала и т.д.;
– по пройденным темам формулирование конкретных ответов на вопросы с объяснениями;
– нахождение нескольких способов решения поставленной задачи, выбор лучшего, т.е. оптимального варианта, исходя из критериев и требований;
– для решения конкретного задания необходима связь с другими обучающимися и преподавателями;
– навыки планирования своих действий и правильное распределение своего времени;
– самооценка результатов деятельности.
Для формирования у студентов предметных и базовых компетенций в процессе учёбы выбран деятельностный подход. Этот подход помогает формировать у студентов опыт самообразования, и они ясно ставят перед собой цели, чем и достигается процесс образования. В основном студенты учатся самостоятельно, планируют и организуют свое время, и дают оценке своих действий. Для достижения вышеназванных целей мною на уроках применяются разные педагогические технологии: дифференцированного обучения.
При данном виде обучения, студенты для изучения нового материала, делятся на три разных по уровням группы.
Компетентностный подход к образованию мотивирует преподавателей разрабатывать и внедрять в практику новые педагогические технологии, парциальные программы, методики, которые должны отвечать современным запросам образования. В связи с чем был разработан рабочая тетрадь по математическому анализу, куда включены вопросы контроля, тесты, темы для практических занятий, тесты для самоконтроля [4].
В основном выделяют два компетентностного подхода в обучении:
1. Современные образовательные технологии: ролевые и деловые игры, написание кейсов, дифференцированный подход и др.
2. Компетентностно-ориентированные задания требуют при решении реальных задач умения применять полученные знания и навыки на практике.
Компетентностный подход в процессе обучения предполагает возможность проблемного подхода, основанного на создании проблемных ситуаций и необходимость самостоятельных действий студентов по их разрешению. Вместе с тем продуктивным является использование студентами индивидуальных и групповых проектов, с помощью которых предполагают самостоятельную работу студентов, и это актуально в случае сокращения аудиторских часов.
Для студентов составлены рабочие тетради по математическому анализу, где для мотивации студентов включены «компетентностно-ориентированные задачи».
Структура задания:
1. Стимул (заставляет понять смысл задания и мотивирует на его решения).
2. Задачная формулировка (указывает на точные действия обучающегося, которая необходима для выполнения задания).
3. Источник информации (сбор информации, необходимой для деятельности обучающегося при выполнении задания).
4. Тетрадь для выполнения задания (определяет структуру для предъявления студенту результатов своей деятельности при выполнении задания).
При применении вышеназванной структуры заданий в работе студента, достигается слаженный механизм компетентностного подхода.
Рабочая тетрадь по математическому анализу состоит из трех групп: «А» – первый уровень, «В» – второй уровень, «С» – третий уровень.
В группе «А» студент совместно с преподавателем выполняет задачу из рабочей тетради, в котором имеются 120 задач и примеров.
В группе «В» студенты применяют репродуктивный метод при изучении нового материала, то есть работу с книгой (студент получает вопросы из рабочей тетради, решает задачи их предложенных 140 задач с применением учебников и делает соответствующий вывод).
В группе «С» студенты занимаются с новым материалом самостоятельно (группа решает задачи из рабочей тетради, из предложенных 160 задач и примеров, выделяя закономерности и делая выводы). В итоге при использовании эвристического метода обучения, самосовершенствовании, у студентов формируются аналитические, творческие и социальные компетенции. Отличием дифференциального метода обучения является то, что на следующем этапе «Применения знаний» студенты первой группы «А» наравне с группой «С» применяют полученные знания.
При этом преподаватель, создав ситуацию успеха, без снисхождения, объективно оценивает ответы. На данном этапе студенты занимаются самостоятельно с самопроверкой (работа дифференцирована по группам).
На рисунке вы видите фрагмент рабочей тетради по математическому анализу, составленной автором на кыргызском языке [5].
Группа А.
Найдите пределы.
а) 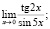
б) 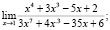
в) 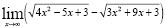 .
.
Группа В.
Найдите пределы.
а) 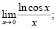
б) 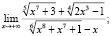
в) 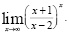
Группа C.
а) Исследуйте непрерывность в этой области
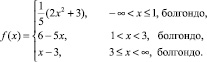
1) 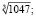 2)
2) 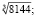 3)
3) 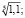 4)
4) 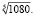 Найти значение. Сравнить результаты.
Найти значение. Сравнить результаты.
б) В конечных и в средней точках дуги АВ окружности проведены касательные и точки А и В соединены хордой. Доказать, что отношение площадей образовавшихся при этом двух треугольников стремится к 4 при неограниченном уменьшении дуги АВ.
в) В круг с радиусом R вписан квадрат, в квадрат вписан круг, в этот круг опять вписан квадрат и так n раз. Найти предел суммы площадей всех кругов и предел суммы площадей всех квадратов при 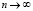 .
.

Фрагмент рабочей тетради по математическому анализу
Техника применения понятия компетенции студентов и преподавателя
|
Пример |
Компетенции студентов |
Компетенции преподавателя |
|
Изучение темы «Вычисление объемов тел» |
1. Умение действовать на занятии |
1. Понимание тематики данной темы. 2. Ориентация в отборе содержания данной темы. 3. Применение активной формы обучения: семинар. 4. Карточки |
|
Пример: Найти объем эллипсоида |
1. Умение правильно спланировать свою работу. 2. Умение пользоваться литературой по данной теме |
Выявление ключевых компетенций у студентов |
|
Решение:
|
Умение правильно решить задачу |
Ориентация методов решения данного задания |
|
Вычисление и результат:
|
Формирование навыков по решению данного задания |
Владение и применение вычисления объема тела по формуле с применением табличных интегралов и формулы Ньютона – Лейбница для вычисления определенных интегралов |
В первой группе включены функции целочисленного аргумента и функции непрерывного аргумента. Решают задачи с последовательным применением существующих правил.
Во второй группе включены с последующим проведением преобразований над функциями, у которых существует предел.
В третью группу включены геометрические и вычислительные задачи.
Задачи взяты из рабочих тетрадей [5] и приведена лишь часть упражнений.
Техника применения понятия компетенции студентов и преподавателя при компетентностном подходе в обучении по математическому анализу приведены в таблице.
Результаты исследования и их обсуждение
Результаты исследования позволили сделать вывод, что применение компетентностного подхода в обучении студентов, компетентностно-ориентированные задания и организация учебного процесса с применением эффективных путей обучения будет способствовать: воспитанию широкого взгляда на жизнь; развитию умения исследовать математическими методами явления реального мира, умения анализировать, обрабатывать информацию и принимать обоснованные решения в различных ситуациях; подготовке к профессиональной деятельности и применении своего опыта в формировании у своих учеников вместе с предметными и ключевых компетентностей.
На основе теоретического анализа трудов ученых определены понятия «компетентностного подхода», «компетенции»; в контексте компетентностного подхода обоснованы и разработаны методические пути обучения математическому анализу студентов вузов педагогического направления, построена техника формирования компетенции; на основе опыта практической деятельности обучения математическому анализу разработаны и систематизированы по группам А, В, С компетентностно-ориентированные задания.
Заключение
При дифференцированном подходе на занятиях по математическому анализу у студентов повышается уровень качества знаний, а также умения и навыки в сфере математического анализа и дает возможность развития рефлекции и формирования контроля над своими действиями. Повышается образованность студентов в преподавании математического анализа и достигается новый уровень знаний по данному курсу.
Компетентностный подход в преподавании математического анализа ведет к повышению уровня образованности студентов и означает достижение нового качества образования. Новое качество образования выражается в новых возможностях выпускников вуза, в их способности решать проблемы, которые предыдущие выпускники не решали.
Применение компетентностного подхода в обучении студентов, компетентностно-ориентированные задания и организация учебного процесса с применением эффективных путей обучения будет способствовать: воспитанию широкого взгляда на жизнь; развитию умения исследовать математическими методами явления реального мира, умения анализировать, обрабатывать информацию и принимать обоснованные решения в различных ситуациях; подготовке к профессиональной деятельности и применение своего опыта в формировании у своих учеников вместе с предметными и ключевых компетентностей.
Исследование позволяет наметить некоторые проблемы, требующие дальнейшей разработки и изучения, а именно:
– совершенствование методической подготовки будущих учителей математики в области оценивания в процессе обучения, в том числе дисциплине «математический анализ».




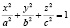
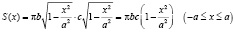
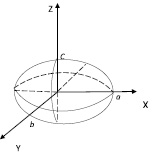
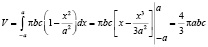 если a = b = c, тогда получим объем шара
если a = b = c, тогда получим объем шара