В настоящее время искусственные нейронные сети успешно применяются в решении биомедицинских проблем – они используются в таких прикладных областях медицины, как функционирование диагностических систем, биохимический анализ, анализ изображений и разработка лекарств.
Среди моделей искусственных нейронных сетей отдельно выделяются нейро-нечеткие сети (ННС), характеризующиеся гибридизацией методологий нечеткой логики и классических нейронных сетей. Диапазон использования нейро-нечетких моделей достаточно широк – прогнозирование, нечеткое управление и классификация. Как правило, системы на базе нечеткого вывода дают лучшие результаты в случае неопределенности и неполноты входных данных или качественных критериев. Согласно крупнейшей библиографической базе статей по медицинским наукам Medline, ННС используются в качестве классификаторов автоматизированных медицинских систем для диагностики опухоли головного мозга, рака молочной железы, остеопороза, глаукомы и т.д.
В обзорной статье, опубликованной в широко известном журнале «Tuberculosis» издательства Elsevier и посвященной использованию разнообразных моделей нейронных сетей для диагностики туберкулеза, затронуты проблемы использования и других методов интеллектуального анализа – нейро-нечетких сетей, генетических алгоритмов и средств имитационного моделирования как «перспективных современных технологических инструментов для борьбы с глобальной угрозой туберкулеза» [1].
Проведенное исследование было направлено на оценку эффективности использования нейро-нечетких моделей для задачи диагностики туберкулеза методом классификации изображений микроскопии препаратов, подготовленных по методу Циля – Нильсена.
Материалы и методы исследования
Медицинские данные были получены у пациентов туберкулезного диспансера и представляют собой цветные изображения, полученные при помощи тринокулярного микроскопа Микромед 1 вар. 3–20 при увеличении 10х60.
В основе функционирования нейро-нечетких систем лежат базовые алгоритмы и методы нейронных сетей, только используются они для поиска параметров нечеткой системы, а именно базы правил, параметров фаззификации и дефаззификации. Сама нейро-нечеткая система ориентирована на аппроксимацию неизвестной n-мерной функции, которая частично определяется данными обучения. Нечеткие правила, закодированные внутри системы, представляют собой нечеткие образцы и нечеткие прототипы данных обучения [2].
В качестве базовых нейро-нечетких систем были рассмотрены системы ANFis и NEFClass, базирующиеся на диаметрально противоположных принципах построения и используемых алгоритмов.
NEFClass
Одна из наиболее популярных систем нейро-нечеткой классификации – это система NEFClass, основанная на обобщенной архитектуре нечеткого перцептрона. Система NEFClass используется для построения нечетких правил из набора данных, обладающих свойством неполноты измерений, которые необходимо разделить на некоторое количество четких непересекающихся классов [3].
Система NEFClass имеет трехслойную архитектуру, состоящую из входного слоя, скрытого слоя с нечеткими правилами и выходного слоя и построена на основе треугольных функций принадлежности. Активация нейронов происходит во втором и третьем слоях по формулам (1) и (2) [4].
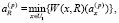 (1)
(1)
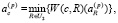 (2)
(2)
где W(x, R) – нечеткий вес соединения входного нейрона х с нейроном правила R, а W(R, с) – нечеткий вес соединения нейрона правила R с нейроном выходного слоя.
Вычислительный эксперимент строился на основе программы NEFClass-PC, которая является свободно распространяемым программным обеспечением. Первичные параметры работы этой системы представлены в табл. 1. Подбор параметров был осуществлен экспериментальным путем.
Система ANFis
Система ANFis (adaptive neuro-fuzzy inference system, адаптивная нейро-нечеткая система) предназначена для моделирования различных типов систем управления, экспертных систем и других сложных систем экономики, сельского хозяйства, медицины и социальных наук. Она является наиболее популярной нейро-нечеткой системой вследствие гибкости, простоты и легкости в понимании основ ее функционирования [5].
Таблица 1
Значение параметров для работы программы NEFClass-PC
|
Параметр |
Значение |
|
Алгоритм генерации правил |
Лучший для класса |
|
Алгоритм обучения |
Классический |
|
Количество термов для каждого признака |
Индивидуально |
|
Функция агрегации |
Взвешенная сумма |
|
Максимальное количество эпох |
500 |
|
Значение параметра сигма |
0,01 |
|
Критерий останова |
Количество эпох, при которых ошибка обучения не уменьшается = 100 |
Система ANFis построена на базе продукционных правил If-Then (Если – То), которые формируют базу нечетких правил выбранной модели. Данная база может быть создана вручную или автоматически сгенерирована системой. В качестве моделей системы выступают три функции – Genfis 1, Genfis 2 и Genfis 3. Все три модели основаны на структуре типа Сугено [6].
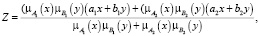 (3)
(3)
где 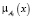 и
и 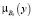 – функции принадлежности, которые могут быть гауссианами (формулы (4) и (5)). Основная задача нейронной сети – подобрать параметры g (формула (6)).
– функции принадлежности, которые могут быть гауссианами (формулы (4) и (5)). Основная задача нейронной сети – подобрать параметры g (формула (6)).
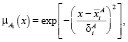 (4)
(4)
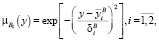 (5)
(5)
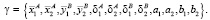 (6)
(6)
Genfis 1 генерирует нейро-нечеткую структуру (FIS) классического типа – с использованием функций принадлежности, где количество правил зависит от количества входов и числа термов. Genfis 2 генерирует FIS, основываясь на методе субстрактивной кластеризации, а Genfis 3 – генерирует нечеткую систему, основываясь на классическом алгоритме кластеризации метода К-средних. Параметры работы моделей Genfis 1 и Genfis 3 приведены в табл. 2 и 3. Подбор параметров также был осуществлен экспериментальным путем.
Таблица 2
Значение параметров для работы функции Genfis 1
|
Параметр |
Значение |
|
Количество термов входных переменных |
2–3 |
|
Тип функции принадлежности |
gaussmf – гауссиана |
|
Тип выходной функции |
constant – константа |
Таблица 3
Значение параметров для работы функции Genfis 3
|
Параметр |
Значение |
|
Количество кластеров |
2 – 3 |
|
Степень перекрытия кластеров |
2 |
|
Максимальное количество операций |
200 |
|
Минимальное приращение функции |
1e-5 |
Вычислительный эксперимент
Перед процедурой классификации исходные изображения были обработаны при помощи операций фильтрации и сегментации. Оптимальными алгоритмами и методами фильтрации и сегментации при этом являются фильтрация при помощи свертки с ядром Гонсалеса 3х3 и сегментация методами FAST и Mexican hat [7, 8]. Результаты предобработки изображений анализов мокроты пациентов специализированного учреждения были представлены в виде текстовых файлов с расширениями .dat и .csv.
Дальнейшие исследования проводились в области построения оптимального вектора признаков по параметрам размерности и информативности в рамках решаемой задачи. В результате были отобраны в качестве классификаторов признаки цвета и формы участков интереса (ROI) – числовые значения параметров цвета RGB, HSV, значения площади и компактности [9].
Для оценивания результатов вычислительного эксперимента применения различных моделей и систем ННС к решаемой задаче были выбраны критерий RMSE (квадратный корень из среднеквадратичного отклонения) и критерии точности и частоты ошибок из-за ограничений программы NEFClass-PC [10]. Под частотой ошибки подразумевается величина, равная отношению суммы критериев FP (количество случаев ложноположительной классификации) и FN (количество случаев ложноотрицательной классификации) к общему размеру исследуемой выборки. Под точностью подразумевается доля правильных ответов алгоритма классификации.
Для проверки качества классификаторов из первичного набора, в связи с ограничениями ННС на количество обрабатываемых данных, генерировалась выборка случайным образом. На каждый классификатор было проведено не менее 10 испытаний. Среднее значение результатов проведенных исследований представлено на рисунке и табл. 4 и 5, где отражена зависимость выбранного параметра сравнения от набора признаков.
Результаты исследования и их обсуждение
Все три модели системы ANFis классифицируют исходный набор данных, сформированный на основе признаков цвета и признаков формы, при этом критерий ошибочной классификации, вне зависимости от размерности вектора признаков и количества записей, не выходит за пределы диапазона значений 9,9–17,8 % (рисунок).
Минимальное значение RMSE, равное 0,27578, система ANFis показала на наборе данных из средних значений цветовых характеристик RGB и HSV, компактности и площадь с использованием модели genfis1 (табл. 4). Максимальное значение точности, равное 85,94 %, система NEFClass показала на том же наборе данных, как и модель genfis1 системы ANFis – 90,1 % (табл. 5).
Исследования проводились на персональном компьютере со следующими характеристиками: процессор Intel® Core™ i7, 2,70 GHz, оперативная память 10,00 ГБ, 64-разрядная операционная система Microsoft Windows 7. При этом часть вычислений не давала результатов по причине переполнения памяти из-за проблемы проклятия размерности (табл. 4–5).
Выводы
Применение нейро-нечетких моделей классификации к задаче диагностики туберкулеза при помощи микроскопии по методу Циля – Нильсена может обеспечить результаты, которые могут соответствовать качеству тех, которые получены с помощью других методов, таких как дискриминационный анализ или нейронные сети.
Таблица 4
Сравнение моделей ННС по параметру RMSE
|
Genfis 1 |
Genfis 2 |
Genfis3 |
NefClass |
|
|
Средние значения HSV, максимальное значение HSV, минимальные значения HSV, компактность, площадь |
Out of memory |
0,29 |
Out of memory |
0,4569 |
|
Средние значения HSV, максимальное значение H, минимальные значения SV, компактность, площадь |
Out of memory |
0,28586 |
Out of memory |
0,379962 |
|
Средние значения RGB и HSV, компактность, площадь |
0,27578 |
0,277 |
0,29741 |
0,2344 |
|
Средние значения R и H, компактность, площадь |
0,30067 |
0,30338 |
0,334 |
0,3579 |
|
Средние значения RGB и HSV, 4 характеристики размеров и компактности, площадь |
Out of memory |
0,276 |
0,29599 |
0,25 |
|
Средние значения HSV, компактность |
0,35063 |
0,35352 |
Out of memory |
0,4029 |
|
Средние значения RGBH, компактности, площадь |
0,27147 |
0,29208 |
0,29782 |
0,4088 |
Таблица 5
Сравнение моделей ННС по параметру точности классификации
|
Genfis 1 |
Genfis 2 |
Genfis3 |
NefClass |
|
|
Средние значения HSV, максимальное значение HSV, минимальные значения HSV, компактность, площадь |
Out of memory |
88,9 % |
Out of memory |
79,87 % |
|
Средние значения HSV, максимальное значение H, минимальные значения SV, компактность, площадь |
89 % |
89,3 |
Out of memory |
85,76 % |
|
Средние значения RGB и HSV, компактность, площадь |
90,1 % |
89,7 % |
88,4 % |
85,94 % |
|
Средние значения R и H, компактность, площадь |
88,4 % |
87,9 % |
86,1 % |
81,98 % |
|
Средние значения RGB и HSV, 4 характеристики размеров и компактности, площадь |
Out of memory |
89,9 % |
88,5 % |
83,97 % |
|
Средние значения HSV, компактность |
82,3 % |
82,2 % |
Out of memory |
70,63 % |
|
Средние значения RGBH, компактности, площадь |
90 % |
88,3 % |
88,8 % |
73,1 % |
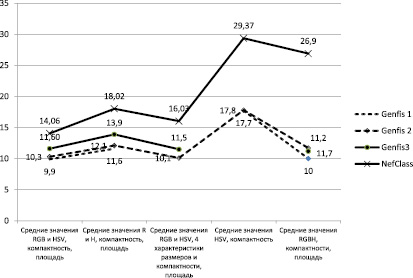
Сравнение моделей ННС по параметру частоты ошибочной классификации
Нейро-нечеткие системы чувствительны к проблеме проклятия размерности – модель genfis1 к размерности вектора признаков, модель genfis3 – к объему обрабатываемых данных. Система NEFClass ограничена как с точки зрения объема обрабатываемых данных, так и чувствительна к их набору. Поэтому при использовании нейро-нечетких систем нужно тщательно подходить к выборке исходных и тестовых данных, проводя дополнительные исследования по оценке количества объектов, достаточных для описания исследуемого процесса.
Для дальнейшей работы с системой NEFClass необходима ее оптимизация путем моделирования нечеткого перцептрона средствами современных систем и средств программирования. Для повышения точности результатов можно использовать генетические алгоритмы и оптимизацию базы правил за счет внедрения многослойной структуры.



