Проведенные в представленной работе исследования относятся к проблемам диагностики технических конструкций, и это направление в настоящее время имеет широкое научное и практическое развитие и применение [1–3]. По акустическому отклику механических систем или их составляющих в виде балок, стержней, дисков и т.д. можно восстанавливать различного рода неисправности таких систем, в том числе учитывающих влияние условий закреплений на их колебательный процесс. Данная работа продолжает подобные исследования и относится к области акустической диагностики механических систем [4–6].
Собственные поперечные колебания различных балок рассматриваются во многих научных работах по теории колебаний, например в [1, 2]. В данной же работе разрабатывается модель балки, состоящей из двух сегментов разного поперечного сечения с учетом условий их сопряжения. Исследована зависимость частот колебаний двухсегментной балки от коэффициентов жесткостей пружин кручения ее шарнирных опор. Поставлена также обратная задача восстановления жесткостей пружин кручения опор балки по конечному набору частот ее поперечных колебаний. Исследованы вопросы существования и единственности решения обратной задачи, представлена соответствующая теорема. Полученный алгоритм решения обратной задачи использует известные значения трех первых частот колебаний сегментной балки.
Прямая задача определения частот поперечных колебаний балки из сегментов
Приведем теоретические сведения по прямой спектральной задаче. Рассмотрим балку длины L ступенчато-переменного сечения с двумя участками разной жесткости EI1 и EI2 длиной l1 и l2 соответственно (рисунок, а). Разность в жесткости между участками образуется в результате поворота правой части относительно левой на угол φ (рисунок, б).
Согласно расчетной схеме балку моделируем сопряжением двух сегментов в виде стержней длиной li. Вводим локальные координаты xi(i = 1,2).
Уравнения свободных поперечных колебаний имеют вид
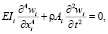(i = 1,2). (1)
В (1): wi = wi(xi, t) – прогиб i-го сегмента;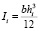 
и Ai = bihi – момент инерции и площадь сечения i-го сегмента; ρ – плотность материала балки. При моделировании также учитываем, что: I2 = α4I1, 
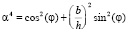, A1 = A2 = A.
От размерных физических параметров переходим к следующим безразмерным: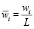 
, 
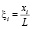, τ = ω0t, 
, 
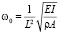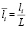, тогда уравнения (1) примут вид
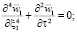
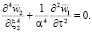(2)
С учетом моделирования свободных поперечных колебаний сегментной балки примем в уравнениях (2) прогиб в ви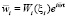де 
, где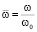 
– безразмерная частота колебаний. Принятые решения 
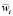подставим в уравнения (2) и с помощью стандартного разделения переменных придем к следующим уравнениям для сегментов:
; 
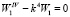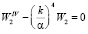. (3)
В (3) введен спектральный коэффициент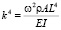 
. Найдем решения уравнений (3):
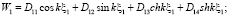
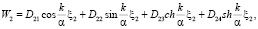(4)
в которых Dij (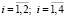
) – амплитуды колебаний двухсегментной балки.
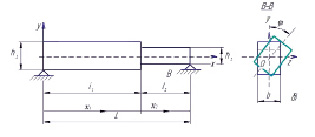
Модель балки ступенчато-переменного сечения
Вместе с дифференциальными уравнениями (1) (или (3)) рассмотрим краевые условия в виде шарнирных опор балки с коэффициентами жесткости c1 и c2 пружин кручения:
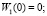
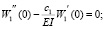
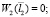
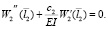(5)
Рассмотрим также условия сопряжения двух сегментов балки разного поперечного сечения, которые при нашем моделировании примут вид
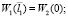
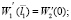
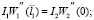
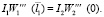(6)
Подставляя решения (4) в краевые условия (5) и условия сопряжения (6), получим систему восьми однородных алгебраических уравнений относительно амплитуд колебаний балки.
Решая полученную систему уравнений относительно ненулевых амплитуд колебаний сегментной балки, получим следующий частотный определитель восьмого порядка:
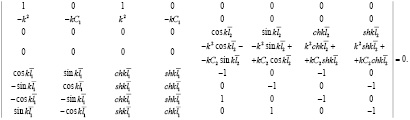(7)
Отметим, что в (7) учтены равенства: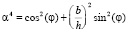 
, Ai = bihi, 
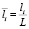, bi = hi,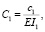 
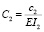. Составлена программа с применением команд математического пакета Maple, с помощью которой по уравнению (7) при заданных значениях жесткостей пружин на кручение шарнирных опор двухсегментной балки и известных ее физических параметрах определяются частоты поперечных ее колебаний.
Проведенные расчеты показывают, что при увеличении жесткостей пружин на кручение частоты колебаний балки увеличиваются. В таблице, например, даны пять собственных значений задачи (3), (5), соответствующие увеличивающимся значениям коэффициента C1 (при C2 = const) при параметрах балки: I1 = I2 = I = 0,5•10-5 м4, l1 = l2 = 0,5 м,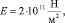 
b = h = 0,1 м.
Зависимость собственных значений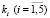 
задачи (3), (5) от коэффициента C1 (при C2 = const)
|
C1 |
C2 |
k1 |
k2 |
k3 |
k4 |
k5 |
|
1 |
1 |
6,2831 |
12,5664 |
18,8496 |
21,9911 |
28,2743 |
|
1,5 |
1 |
6,3157 |
12,5844 |
18,8620 |
22,0019 |
28,2828 |
|
2 |
1 |
6,3456 |
12,6016 |
18,8740 |
22,0124 |
28,2911 |
|
2,5 |
1 |
6,3731 |
12,6182 |
18,8858 |
22,0226 |
28,2993 |
|
3 |
1 |
6,3985 |
12,6341 |
18,8972 |
22,0326 |
28,3073 |
Проведенные исследования важны при рассмотрении проблемы сохранения безопасных частот колебаний сегментной балки.
Обратная задача диагностирования жесткостей пружин на кручение опор балки
Смоделируем теперь обратную задачу, а именно задачу акустического определения жесткостей пружин на кручении шарнирных опор балки. Итак, известен конечный набор частот поперечных колебаний сегментной балки, необходимо восстановить жесткости пружин на кручении ее шарнирных опор.
Преобразуем частотное уравнение (7) к следующему виду относительно искомых параметров C1 и C2:
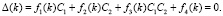(8)
Введенные в рассмотрение в (8) функции fi(k)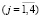 
зависят от физических параметров балки, а также спектрального параметра 
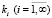следующим образом:
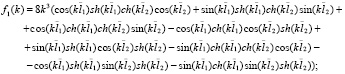
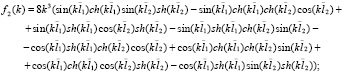
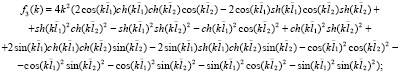
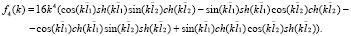(9)
Для исследования вопроса о существовании решения обратной задачи введем в рассмотрение две спектральные задачи L и L' с соответствующими частотными уравнениями Δ(k) (равенство (7)) и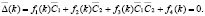 
Отметим, что уравнение 
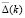имеет те же функции (9), но другие безразмерные коэффициенты 
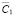и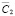 
. Сформулируем теперь теорему.
Теорема. Пусть частотные уравнения Δ(k) и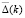 
задач L и L' имеют вещественные корни 
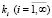(а значит, собственные частоты 
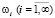). Тогда при совпадении 
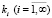с учетом их кратностей будут совпадать и коэффициенты: 
, 
.
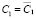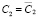Доказательство. Заметим, что частотные уравнения Δ(k) и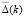 
являются целыми функциями от параметра 
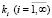. Кроме того, с помощью команд математического пакета можно показать, что Δ(k) и 
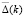являются линейно независимыми функциями. Тогда с учетом теоремы Адамара [7] можно утверждать, что ненулевые целые функции Δ(k) и 
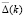восстанавливаются по параметру 
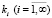с точностью до постоянного множителя К: 
– 
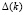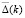= 0. В итоге получаем, что K = 1, откуда: 
, 
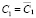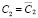. Теорема доказана.
Метод решения обратной задачи
Проведенные исследования по вопросу единственности решения обратной задачи позволяют определять безразмерные коэффициенты C1 и C2 (а значит, и жесткости c1 и c2 пружин на кручение шарнирных опор балки) единственным образом. Необходимо теперь построить алгоритм решения задачи.
Покажем, что для единственности восстановления искомых параметров достаточно знание первых трех значений собственных частот ωi поперечных колебаний двухсегментной балки. Для этого с учетом вида частотного уравнения (8) введем дополнительный параметр D = C1C2. Тогда при известных значениях ki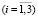 
получим систему уравнений
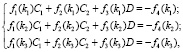(10)
в которой C1, C2 и D неизвестны, а функции fi(k)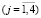 
определяются при ki 
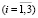формулами (9). Решая (10) методом Крамера, получим
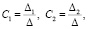(11)
где
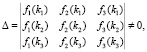
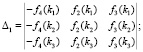
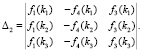(12)
С учетом введенной переменной необходимо проверить также выполнение равенства:
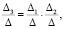
в котором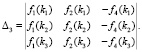 
Таким образом, найденный алгоритм решения системы уравнений (10) позволяет однозначно восстанавливать искомые коэффициенты C1, C2 по аналитическим формулам (11)–(12) при известных трех ненулевых собственных частотах ωi колебаний двухсегментной балки.
Применение метода рассмотрим на конкретном примере.
Пример. Даны собственные значения k1 = 9,26658, k2 = 12,43919, k3 = 18,75845, соответствующие первым трем частотам колебаний балки ступенчато-переменного сечения, а также физические параметры: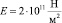 
; I1 = I2 = I = 0,5•10-5 м4; l1 = l2 = 0,5 м; b = h = 0,1 м. Найти коэффициенты жесткости c1 и c2 пружин на кручение шарнирных опор балки. Подставляя значения k1, k2, k3, а также заданные физические параметры в (9), получим
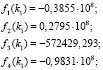
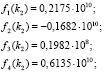
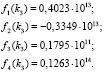
Далее по формулам (10), (11) имеем: Δ = 0,3876•1026; Δ1 = 0,3876•1026; Δ2 = 0,1938•1027. Тогда определяем следующие безразмерные параметры: С1 = 1; С2 = 5, через которые находим значения коэффициентов жесткостей опор балки: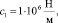 
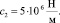
Заключение
В работе была исследована и решена прямая задача определения поперечных колебаний балки из двух сегментов при шарнирных опорах с пружинами кручения различной жесткости. Исследовано влияние на собственные частоты колебаний сегментной балки коэффициентов жесткостей ее опор и установлена прямая зависимость при любых ее других физических параметрах. Приведена постановка обратной спектральной задачи, исследован вопрос существования и единственности ее решения. Алгоритм решения обратной задачи сведен к введению новой переменной с последующим решением системы трех линейных уравнений относительно искомых параметров. Получены математические модели для определения коэффициентов жесткости шарнирных опор сегментной балки единственным образом.
Исследование выполнено при финансовой поддержке РФФИ и Правительства Республики Башкортостан в рамках научного проекта № 17-41-020230-р_а.