Указание границ толерантных интервалов является одним из основных условий международной сертификации промышленных изделий.
Толерантный интервал – интервал, определяемый по выборке, относительно которого можно утверждать с уровнем доверия γ, что он содержит, по крайней мере, указанную долю p0 совокупности.
Границы статистического толерантного интервала – толерантные границы.
Уровень доверия γ = 1 – α – это вероятность того, что толерантный интервал будет содержать не менее p0•100 % совокупности.
Вероятность попадания СВ Х с функцией распределения FX(x) в интервал [L, U] равна FX(U) – FX(L). То есть границы толерантного интервала – это решение уравнения
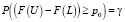
для двустороннего интервала [L, U] и
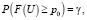
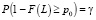
для односторонних интервалов (–∞; U] и [L; +∞) соответственно.
Обычно двусторонние толерантные интервалы ищутся в форме [M – kσ; M + kσ], односторонние – в форме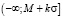 
или 
.
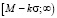На данный момент достаточно полно изучен вопрос оценки толерантных пределов, как двусторонних, так и односторонних, для некоторых известных распределений.
Так, в работах [1] выводятся оценки толерантных пределов нормально распределенной генеральной совокупности, в работах [1, 2] рассматриваются оценки толерантных пределов показательно распределенных совокупностей. В ряде работ предлагаются оценки толерантных границ для распределений Вейбула, Гаусса, логнормального распределения [3] сведением их к нормальному распределению.
Но в некоторых случаях априори вид распределения неизвестен. В этом случае необходимо либо предварительно выдвинуть гипотезу о виде распределения и проверить ее, что в случае ограниченной информации может вызвать затруднения, либо использовать непараметрические критерии для требуемых оценок.
Значительная часть результатов математической статистики основана на предположении о том, что информации, имеющейся у потребителя, достаточно для представления участвующих в задаче распределений в виде некоторых функций с конечным числом параметров. Однако на практике это предположение часто оказывается невыполнимым. Потребности в создании статистических процедур, не предполагающих знание вида распределений, отвечает ветвь математической статистики, получившая название непараметрическая статистика. Непараметрическая статистика рассматривает только такие ситуации, в которых о функциональном виде распределений ничего не известно. Теория непараметрического оценивания плотности распределения широко представлена в работах Л. Девроя и Л. Дьёрфи, Парзена, Розенблатта, Ш. Закса, Хансена и Кумпенса. Обзор укакзанных методов приведен в [2]. Оказалось, что, несмотря на малый объем априорной информации, используемой при построении непараметрических процедур, они обладают высокой эффективностью. Потери эффективности при переходе от параметрических к непараметрическим процедурам (в случае истинности параметрической модели) незначительны и довольно часто составляют всего несколько процентов. Эффективность непараметрической процедуры по сравнению с фиксированной параметрической резко возрастает при отклонении истинных распределений от расчетных. В большинстве случаях непараметрические процедуры оказываются асимптотически оптимальными.
Материалы и методы исследования
Широко известна [2] непараметрическая оценка толерантных границ с использованием β-распределения. Для упорядоченной выборки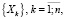 
из произвольно распределенной генеральной совокупности решение неравенства 
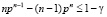определяет долю p генеральной совокупности, попадающей в интервал 
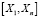с вероятностью γ. Но полученная таким образом оценка жестко связывает долю p, доверительную вероятность γ и объем выборки n. То есть при одном и том же объеме выборки увеличение доли p ведет к уменьшению доверительной вероятности γ и наоборот.
Теория непараметрических доверительных и толерантных интервалов развивалась в исследованиях Уилкса, Оуэна, Гаттмена, Роббинса, Фрэзера, Барлоу и Прошана, Хансона и Кумпенса и других. В этих работах строятся функции специального вида, мажорирующие вероятность попадания случайной величины в заданный интервал, представленной в виде упорядоченной статистики. В основном эти оценки связаны с β-функцией.
В работах Хансена и Купменса [2] предлагается искать верхнюю толерантную границу для выборки Xi в виде
,
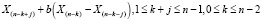где коэффициент b является решением уравнения
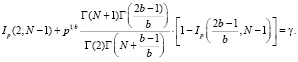
В ряде отечественных работ [3–5] для непараметрических оценок используется ядерный метод получения функции распределения. Согласно указанной методике, функция плотности вероятности рассматриваемой случайной величины определяется формулой
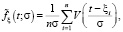(1)
где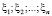 
– выборка, полученная в результате наблюдений за исследуемым объектом; n – объем выборки; 
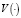– ядерная функция, удовлетворяющая условиям регулярности
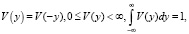
σ > 0 – параметр сглаживания, такой, что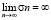 
.
В качестве ядерной функции чаще всего выбираются следующие функции [6]:
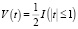– прямоугольное ядро;
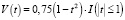– ядро Епанечникова;
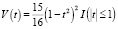– квадратическая ядерная функция.
В рассматриваемых функциях 
Точность оценки зависит как от выбора функции-ядра, так и выбора параметра сглаживания. В работе [7] предложена методика поиска оптимального значения параметра сглаживания.
В работе [6] получена оценка доверительного интервала для теоретической функции плотности вероятности при n ≥ 100
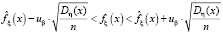
и при небольших значениях n ≤ 100:
.
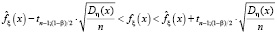Результаты исследования и их обсуждение
Рассуждая аналогично [6], проведем оценку одностороннего толерантного интервала. Обозначим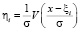 
. Случайные величины ηi при каждом x независимы.
Согласно центральной предельной теореме, при больших значениях n, оценка функции плотности вероятности, как суммы независимых величин, является при каждом x нормально распределенной случайной величиной, т.е.
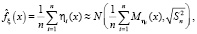
где
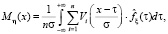
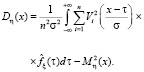(2)
Соответственно, случайная величина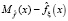 
имеет нормальное распределение с нулевым математическим ожиданием и той же дисперсией:
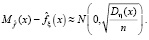
Тогда
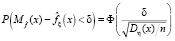
и при доверительной вероятности β:
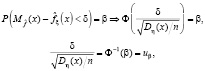
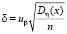
(uβ – β-квантиль стандартного нормального распределения).
Окончательно получаем, что с вероятностью β верна оценка
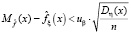
или
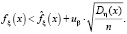
При небольших значениях n используется распределение Стьюдента с n – 1 степенью свободы, т.е.
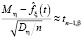
и
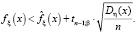(3)
Пусть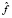 
– оценка функции плотности вероятности f для случайной величины X, представленной выборкой 
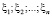. Оценка L нижней толерантной границы для доли p0 с доверительной вероятностью γ является решением уравнения
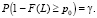(4)
Проинтегрировав неравенство (3) и выполнив необходимые оценки, получим
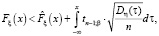
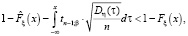
где
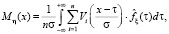
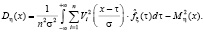
Другими словами, неравенство
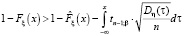
верно с вероятностью β. Тогда, если верно неравенство
,
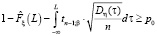то с вероятностью β будет верно неравенство
,
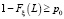т.е.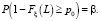 
Следовательно, уравнение (4), определяющее значение оценки нижней границы L одностороннего толерантного интервала, верно в случае, если β = γ. Таким образом, оценку границы левостороннего толерантного интервала для доверительной вероятности γ можно найти как решение неравенства
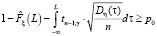(5)
при n ≤ 100 и неравенства
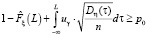(6)
при n > 100.
Таким образом, получен алгоритм построения нижней толерантной границы с помощью ядерной оценки функции плотности.
1. Оценить выборочное среднее, выборочную дисперсию СВ, представленной выборкой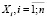 
. Выбрать оптимальное значение параметра сглаживания.
2. Найти промежутки ненулевых значений ядер: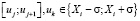 
.
3. Определить на каждом из промежутков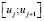 
функцию
.
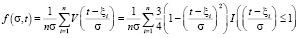4. Определить на каждом из промежутков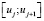 
функцию F(x):
.
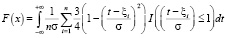5. Определить значение статистики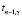 
.
6. Определить дисперсию оценки по формуле (1).
7. Найти нижнюю толерантную границу, решив неравенство (5) ((6)).
Заключение
Для апробации была рассмотрена выборка, полученная в результате усталостных характеристик 78 экспериментальных образцов. Варианты выборки принадлежали отрезку [195, 230]. Были получены оценки нижней толерантной границы для γ = 0,95, p = 0,9 а) по формулам для случая нормально распределенной генеральной совокупности L = 191,44, б) по методу Хансена – Кумпенса L = 144,15, в) по предложенному алгоритму ядерной оценки L = 188,1.