Интегральные динамические модели широко используются для описания и моделирования технических систем [1, с. 12–18]. В случае стационарной системы применяется уравнение Вольтерра I рода вида [2, с. 25–29]
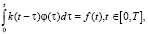(1)
где k(t) – импульсная переходная функция (ИПФ) системы (ядро интегрального уравнения); φ(τ), f(t) – входной и выходной сигналы системы. При этом выполняется условие, которое определяется технической реализуемостью системы
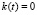при 
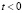. (2)
Задача непараметрической идентификации [2, 3] заключается в построении оценки для k(t) по зарегистрированным значениям входного и выходного сигналов идентифицируемой системы. Заметим, что найденная оценка ИПФ в дальнейшем используется как для вычисления количественных характеристик системы (время переходного процесса, величина перерегулирования и т.д.), так и для моделирования системы в целом с использованием модели «вход-выход».
Задача идентификации является некорректно поставленной (НПЗ), в которой может нарушаться одно или несколько требований корректности задачи по Адамару [4, с. 15–18]. Для вычисления устойчивого единственного решения НПЗ используются различные (детерминированные или статистические) регуляризирующие алгоритмы (РА). Для применения РА исходное уравнение или аппроксимируют системой линейных алгебраических уравнений с плохо обусловленной матрицей, или заменяют дискретной сверткой и строят РА на основе дискретного преобразования Фурье (подробнее см. [5, с. 102–106]). И в том, и в другом случаях возникают принципиальные трудности, приводящие к увеличению ошибки идентификации (отсутствует возможность в РА учесть случайный характер погрешностей измерений входного сигнала, сложность формирования периодической дискретной свертки [5, с. 103–106], значительная ошибка аппроксимации исходного интегрального уравнения при невозможности задать требуемый шаг дискретизации и другие).
В данной работе предлагается новый устойчивый алгоритм идентификации, основанный на сведении уравнения (1) к интегральному уравнению II рода (решение которого является корректно поставленной задачей), в которое входят первые производные от входного и выходного сигналов (вычисление которых является НПЗ). Для устойчивого вычисления производных предлагается использовать кубические сглаживающие сплайны, а ошибки дифференцирования минимизируются за счёт выбора параметра сглаживания на основе излагаемого критерия оптимальности. Все это позволяет существенно уменьшить влияние погрешностей регистрации входа и выхода системы на точность получаемых решений задачи идентификации ИПФ стационарной системы.
Метод исследования
Для построения устойчивого алгоритма решения задачи идентификации приведём уравнение (1) к виду уравнения задачи идентификации. При выполнении условия (2) получаем
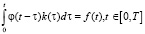. (3)
Дифференцируя это уравнение по переменной t и выполнив несложные преобразования, приходим к интегральному уравнению Вольтерра II рода
,
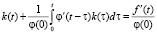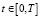(4)
решение которого уже является корректно поставленной задачей. Однако построение алгоритма вычисления k(t) из этого уравнения сталкивается со следующими основными трудностями: дифференцирование зашумлённых входного и выходного сигналов идентифицируемой системы; вычисление интеграла свёртки с наименьшими ошибками интегрирования для уменьшения общей систематической ошибки алгоритма идентификации. Для преодоления этих трудностей привлечём математический аппарат сглаживающих кубических сплайнов (СКС). Приведём только основные понятия СКС, необходимые для дальнейшего изложения алгоритма идентификации.
Предположим, что на некотором интервале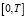 
заданы N узлов
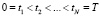(5)
и определены значения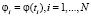 
функции φ(t) в этих узлах. Функция Sφ(x) называется кубическим сплайном с узлами (5), если:
а) на каждом интервале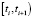 
функция Sφ(t) является кубическим многочленом вида
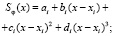(6)
б) функция Sφ(t) дважды непрерывно дифференцируема на всём интервале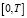 
.
Сплайн называется интерполяционным, если выполняются условия интерполяции
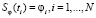. (7)
Естественным сглаживающим кубическим сплайном называется функция S φ, α(t), удовлетворяющая естественным краевым условиям на вторую производную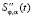 
: 
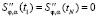и доставляющая минимум функционалу [6, с. 42–44; 7, с. 124–132]:
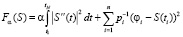, (8)
где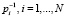 
– весовые множители. Как видно из (8), сглаживающий сплайн не проходит через значения φi и поэтому он используется для фильтрации (сглаживания) зашумлённых значений. Параметр сглаживания α «управляет» гладкостью сплайна (а следовательно, и ошибкой сглаживания):
- при α = 0 сглаживающий сплайн становится интерполяционным (т.е. проходит через все заданные точки φi);
- при α→∞ сглаживающий сплайн вырождается в прямую линию (эффект переглаживания зашумленных данных).
Алгоритм вычисления коэффициентов сглаживающего сплайна при заданном α подробно изложен в [6, с. 45–49] и здесь не приводится. Для построения алгоритма решения уравнения (4) временно будем считать, что по зашумлённым значениям входного и выходного сигналов
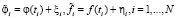, (9)
где ξi, ηi – случайные погрешности регистрации сигналов с дисперсиями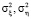 
соответственно построены сглаживающие кубические сплайны S φ, α(t), S f, α(t) с производными 
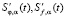соответственно.
Обратимся к интегралу свёртки, входящему в уравнение (4). Для вычисления оценки для k(t) предположим, что на каждом интервале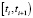 
k(t) постоянно и равно 
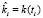. Тогда, используя производную 
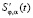сглаживающего сплайна, интеграл свёртки будем аппроксимировать суммой
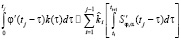. (10)
Можно показать, что
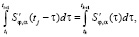(11)
где k = j – i. Подставляя (11) в (10), получаем
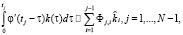(12)
где Фj,i – элементы матрицы Ф, определяемые через коэффициенты сплайна S φ, α(t):
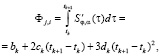(13)
где k = j – i. Таким образом, матрица Ф имеет размер (N – 1)×(N – 1), и если i > j, то Фi,j = 0. Заметим, что полученная квадратурная формула (13) позволяет достаточно точно и эффективно вычислять значения интегралов, тем самым уменьшая методическую ошибку предложенного алгоритма. Сформируем векторы
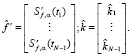
Тогда уравнение (4) можно аппроксимировать следующей системой линейных алгебраических уравнений (СЛАУ) вида
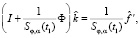(14)
где I – единичная матрица размером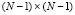 
. Решая эту систему, получаем вектор 
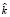, проекции которого являются оценками для значений k(ti) идентифицируемой ИПФ системы.
Заметим, что СЛАУ (14) имеет хорошо обусловленную матрицу (число обусловленности не больше 3–5), и точность идентификации определяется только ошибками дифференцирования входного (элементы матрицы Ф) и выходного (проекции вектора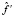 
) сигналов.
От величины параметра сглаживания α существенно зависит ошибка сглаживания. Очевидно желание выбрать параметр таким, чтобы его значение минимизировало принятую величину ошибки сглаживания, которую определим как среднеквадратическую ошибку сглаживания
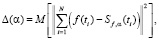(15)
где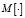 
– оператор математического ожидания. Для вычисления оптимального значения αopt необходима априорная информация о точных значениях f(ti), которая на практике, естественно, отсутствует.
В работе [6, с. 60–73] рассмотрены несколько алгоритмов выбора параметра сглаживания. Показано, что эффективной (наилучшей) оценкой для αopt является величина αW, вычисленная на основе статистического критерия оптимальности фильтрации зашумлённых данных. Обоснование этого критерия и его свойства подробно изложены в [6, с. 62–67]. Здесь приведём только конечные соотношения, необходимые для вычисления оценки αW.
Введём в рассмотрение статистику
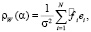(16)
где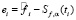 
– невязка i-го измерения. Доказано, что если ρW(α) при некотором значении α удовлетворяет неравенству
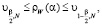(17)
то такое значение можно принять в качестве оценки для αopt (обозначим это значение как αW). В неравенстве (17) величины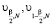 
– квантили χ2-распределения с N степенями свободы уровней 
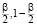соответственно. Величина β определяет вероятность ошибки первого рода при проверке гипотезы об оптимальности оценки αW и, как правило, β = 0,05.
Заметим, что вычисление αW сводится к решению нелинейного уравнения
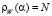(18)
итерационными алгоритмами. В качестве αW принимается очередное приближённое решение α(n) , которое удовлетворяет неравенству (17). Эффективный алгоритм вычисления αW, построенный на основе метода Ньютона, приведён в [6, с. 65–66]. Выполненные исследования точности оценки αW [6, с. 72–76] показали, что сплайн, построенный при α = αW , имеет:
а) ошибку сглаживания, незначительно (на 5–8 %) превышающую ошибку сглаживания при параметре α = αopt (который можно найти только в вычислительном эксперименте);
б) ошибку сглаживания, значительно (на 15–35 %) меньше по сравнению с другими способами выбора параметра (подробнее см. [6, с. 73–76; 8, 9]).
Всё это позволяет сделать вывод о целесообразности использования сглаживающего сплайна с α = αW для устойчивого вычисления производных входного и выходного сигналов при формировании матрицы Ф и вектора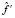 
системы (14).
Результаты численных исследований
Для проверки работоспособности и эффективности предложенного алгоритма идентификации был проведен многочисленный вычислительный эксперимент. Остановимся только на результатах одной серии исследований. В качестве k(t) была взята ИПФ колебательного звена второго порядка (на рис. 1 – сплошная кривая). Значения входного и выходного сигналов искажались случайными нормально распределенными погрешностями с относительными уровнями: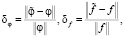 
где φ, f – векторы, составленные из точных значений сигналов, 
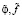– векторы зашумленных значений, 
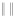– евклидова норма вектора. Ошибка идентификации определялась относительной величиной 
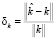. На рис. 2 точечной кривой показана оценка для ИПФ, построенная по производным интерполяционных сплайнов (т.е. без сглаживания) при уровнях шумов δφ = 0,05, δf = 0,05, N = 190, сплошной кривой – значения точной ИПФ. Видно, что полученное решение существенно отличается от точной ИПФ, что иллюстрирует высокую неустойчивость такого решения к погрешностям регистрации входного и выходного сигналов. На рис. 1 точечной кривой показано решение, построенное по сглаживающим кубическим сплайнам (с параметрами сглаживания αW) при тех же уровнях шумов. Видно, что решение достаточно хорошо совпадает с точной ИПФ системы (относительная ошибка идентификации δk = 0,077).
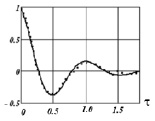
Рис. 1. Импульсная переходная функция и ее оценка
Также было выполнено сравнение предложенного алгоритма идентификации с регуляризирующим алгоритмом, построенным на основе ДПФ (подробно этот РА изложен в [5, с. 104–105]. Относительная ошибка идентификации предложенным алгоритмом была на 25–50 % меньше по сравнению со вторым РА. Это отчасти объясняется ошибкой аппроксимации исходного уравнения системой линейных алгебраических уравнений во втором РА. Заметим, что выигрыш по точности идентификации увеличивался по мере возрастания отношения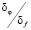 
, например при 
.
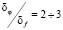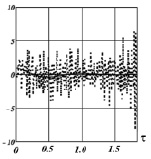
Рис. 2. Оценка ИПФ, построенная по интерполяционным сплайнам
Заключение
Высокая точность предлагаемого алгоритма идентификации объясняется следующими его преимуществами:
1. Матрица СЛАУ (14) хорошо обусловлена, и поэтому ошибки вычисления вектора правой части (ошибки дифференцирования выходного сигнала) гораздо слабее влияют на построенное решение, чем погрешности правой части в РА, построенном на основе ДПФ.
2. Наличие в предлагаемом алгоритме интеграла от производной входного сигнала (при вычислении элементов матрицы Ф (12), (13) в значительной степени «сглаживает» ошибку вычисления первой производной, что обуславливает уменьшение общей ошибки идентификации.