Рассмотрим численные методы GMRES и прямое LU разложение, произведем сравнительный анализ полученных данных методами решений СЛАУ больших размерностей на плотных несимметричных матрицах квадратной формы.
Цель исследования: выявить зависимость между сходимостью рассматриваемых численных методов и размерностью СЛАУ.
Материалы и методы исследования
Вычисления проводились на программной платформе .NET Framework 4.5.1, в качестве IDE использовалась Microsoft Visual Studio 2017. Для реализации метода GMRES за основу был взят github проект участника Dan Lavrushko [1]. LU декомпозиция выполнена с помощью библиотеки Math.NET Numerics [2].
Постановка задачи
Рассмотрим задачу решения СЛАУ A•x = b итерационным методом GMRES [3] и LU разложением (декомпозицией) [4], где: A – невырожденная, плотная, несимметричная матрица размером m×m; x – вектор неизвестных размером m; b – свободные члены размером m (1).
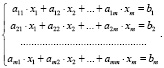(1)
Метод GMRES
Для численного решения произвольных СЛАУ с заданной точностью на невырожденных, плотных и несимметричных матрицах распространено применение итерационного обобщенного метода минимальных невязок (GMRES).
Метод подразумевает использование алгоритма итераций Арнольди [5] с целью нахождения приближенных собственных векторов матрицы посредством построения ортонормированного базиса подпространства Крылова [6] для осуществления аппроксимации решения с минимальной невязкой.
Сам алгоритм метода GMRES был предложен в 1986 г. Юсефом Саадом и Мартином Х. Шульцем. GMRES стал обобщением метода MINRES Криса Пейджда и Майкла Сондерса, также является частным случаем метода DIIS Питера Пулайе, применимым к нелинейным системам.
Из сложности процесса Арнольди, минимизации невязки и матрично-векторного произведения складывается сложность метода GMRES.
Увеличение объема требуемой памяти для покрытия стоимости вычисления собственных векторов на каждой итерации составляет O(n2), где n – номер итерации. Очевидно, что многие вычислительные системы не в состоянии удовлетворить такие потребности алгоритма, поэтому для устранения проблемы производится перезапуск вычислений после заданного значения k итераций, начиная с xk в качестве начального предположения. Такой подход признан модификацией исходного GMRES алгоритма и обозначается с припиской Restarted. При использовании Restarted GMRES возникает существенный недостаток: перезапущенное подпространство часто близко к более раннему подпространству, поэтому метод страдает от стагнации конвергенции. Решением проблемы служит повторное использование подпространства Крылова методами GCROT и GCRODR, которые относятся к типу GCRO.
Сложность решения задачи минимизации невязки (минимальных квадратов) составляет O(m2), где m – размер матрицы.
Сложность получения решения матрично-векторным произведением составляет O(nm).
Математическое описание алгоритма GMRES. На каждом k-м шаге решение xk рассматривается в виде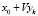 
, где столбцы υk матрицы V находятся с помощью процесса Арнольди для построении ортонормированного базиса 
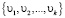подпространства Крылова 
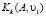, вектор yk представляет собой решение системы 
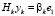, где Hk – верхняя матрица Хессенберга размера k×k, элементы которой формируются в процессе ортогонализации Арнольди, 
, 
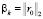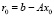, и, наконец, e1 – канонический вектор 
размерности k.
Ортонормированный базис {υ1, υ2,... υk} подпространства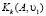 
вычисляется с помощью ортогонализации Арнольди по формулам
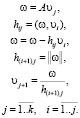(2)
После завершения вычислений процессом Арнольди получаем ортонормированный базис подпространства Крылова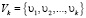 
и матрицу, расширенную последним вычисленным вектором 
: 
.
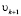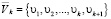Hk – верхняя Хессенбергова матрица, элементы которой равны коэффициентам ортогонализации 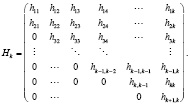(3).
(3)
Выполнив несложные преобразования, можно получить выражение для невязки на k-й итерации: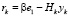 
. Очевидно, что для задачи 
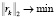минимум достигается при 
.
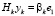Для решения последней системы матрица приводится к верхнему треугольному виду с помощью k вращений Гивенса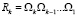 
(4).
(4)
где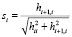 
, 
.
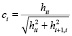Метод LU разложения
LU разложение основывается на методе последовательного исключения Гаусса. Метод LU разложения подразумевает представление исходной матрицы A в виде произведения нижнетреугольной матрицы L на верхнетреугольную матрицу U (5). Традиционно, либо матрица L, либо U нормализуются до получения единичной диагонали. Несмотря на то, что метод LU разложения предназначен для матриц любой (прямоугольной) формы, чаще всего он применяется к квадратным матрицам A•x = b.
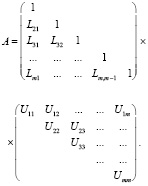(5)
Хорошим свойством LU декомпозиции является то, что для хранения опорных точек достаточно O(m) требуемой памяти, так как элементы матрицы L выше главной диагонали равны нулю (сама матрица L имеет единичную диагональ, в соответствии с классической схемой нормализации), поэтому должны быть сохранены только субдиагональные элементы. Точно так же с матрицей U – элементы ниже главной диагонали равны нулю, поэтому должны быть сохранены только главная диагональ и супердиагональные элементы 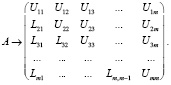(6).
(6)
Таким образом, LU представление матрицы A занимает столько же места, сколько исходная матрица. Исходную матрицу не требуется хранить, так как вся информация о ней расположена в полученных треугольных L и U матрицах.
Различают две реализации алгоритма: наивную и блочно-матричную факторизацию.
Наивная реализация LU разложения плохо масштабируется в зависимости от размера СЛАУ. Когда размерность матрицы A превышает 64×64, она не вписывается в типичную кэш-память ЦП L1, вследствие чего алгоритм затрачивает большую часть времени исполнения на ожидание поступления данных из кэш-памяти L2/L3 или ОЗУ.
Блочно-матричный подход является лучшим решением для решения СЛАУ больших размерностей. При его применении большая матрица разбивается на мелкие блоки и выполняется пошаговая факторизация. Алгоритм LU разложения при таком подходе будет состоять из нескольких шагов.
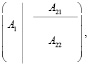
На первом шаге от входящей матрицы m×m производится отделение ведущей подматрицы m×k (7).
(7)
где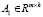 
, 
, 
.
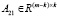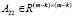На следующем шаге производится LU факторизация наименьшей матрицы m×k, в то время как остальные части остаются неизменными 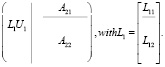(8).
(8)
Сравнительный анализ итерационного метода GMRES с прямым LU разложением
|
Размерность |
GMRES |
LU |
Невязка |
|
Погрешность |
Погрешность |
||
|
100×100 |
2,0116088480075E-12 |
2,11060429475097E-12 |
2,0925483568135E-11 |
|
200×200 |
1,83254249558738E-13 |
5,04210124070489E-13 |
1,3944401189292E-13 |
|
300×300 |
1,95004482511071E-12 |
2,47861082279823E-12 |
3,47103679132488E-10 |
|
400×400 |
2,76235503824824E-13 |
1,1413797766996E-12 |
1,38888900380607E-13 |
|
500×500 |
4,48703350072223E-12 |
1,3246281079378E-11 |
1,64552815817842E-11 |
|
600×600 |
5,9363410406452E-13 |
2,72143384747093E-12 |
7,18314296932476E-14 |
|
700×700 |
1,42739638197509E-12 |
7,78304694683747E-12 |
2,00772731773213E-12 |
|
800×800 |
1,61541324545316E-12 |
8,03706747369854E-12 |
8,83848549904087E-12 |
|
900×900 |
5,80869227195123E-12 |
4,70100645431032E-11 |
3,67883501439792E-12 |
|
1000×1000 |
1,78459029722083E-12 |
1,50275970448393E-11 |
2,58693066967908E-12 |
|
2000×2000 |
8,9116957833455E-11 |
8,4298279402325E-10 |
4,32651248161164E-09 |
|
3000×3000 |
1,02300509221517E-10 |
2,25055203080853E-09 |
3,241424906264E-10 |
|
4000×4000 |
2,11655434842488E-10 |
5,10361178511771E-09 |
1,20999033015323E-09 |
|
5000×5000 |
2,45441089565206E-11 |
7,38593135178026E-10 |
9,10804764941986E-12 |
|
6000×6000 |
4,77423520551148E-11 |
1,13189903713514E-09 |
6,47268016962244E-10 |
|
7000×7000 |
9,69911363063168E-10 |
1,10518722842222E-08 |
1,12652671191427E-07 |
|
8000×8000 |
2,66089964273607E-11 |
1,36072345874094E-09 |
1,36598510280805E-11 |
|
9000×9000 |
4,99308489261675E-11 |
2,23105000993159E-09 |
1,92463156523104E-10 |
Следующий шаг – обновление части матрицы результатами исходной LU. Верхний блок A21 умножается на inv(L11), а конечная матрица A22 получает более сложное обновление 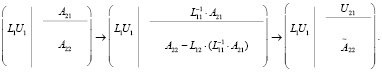(9).
(9)
В результате имеется k столбцов L-фактора в L1, первые k строк U-фактора в матрицах U1 и U21, а оставшаяся часть, подлежащая обработке, A, сохраняется в конечных mk-строках/столбцах. На этом этапе остается только применить алгоритм к конечным строкам/столбцам A, пока не получится факторизация полной матрицы.
В целом подход имеет хороший потенциал для распараллеливания, потому что взаимодействия с большими m и k могут быть эффективно разделены между различными ядрами.
Частными случаями LU разложения являются: метод прогонки (используется для трехдиагональных матриц), факторизация Дулитла (если у матрицы L на главной диагонали все единицы), факторизация Крита (если у матрицы U на главной диагонали все единицы). Когда U = LT (или L = UT), это называется разложением Холецкого.
Результаты исследования и их обсуждение
Программно реализовав описанные выше методы, был проведен численный эксперимент, результаты которого представлены в таблице (в соответствии с таблицей).
Для сравнения поведения методов на СЛАУ больших размерностей на каждом шаге сгенерирована произвольная плотная несимметричная матрица квадратной формы A и массив свободных членов b (1).
Решение итерационным методом GMRES находилось с заранее заданной точностью 1E-3.
Погрешность решения рассмотренными численными методами [7] для каждой размерности СЛАУ находилась по формуле
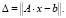(10)
Для проведения сравнительного анализа была найдена максимальная невязка между решениями, полученными представленными методами:
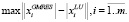(11)
Полученные результаты могут быть использованы при решении задач, поставленных в работах [8–10].
Выводы
Опираясь на результаты невязок, можно сделать вывод, что оба метода сошлись для сгенерированных СЛАУ всех размерностей. Анализируя значения невязок, можно сказать, что наиболее заметна зависимость решений от сгенерированных коэффициентов в исходной матрице. Зависимость между размерностью исходных СЛАУ и значениями невязок решений не обнаружена.