Олимпиадное движение в Кыргызской Республике имеет более чем 50-летнюю историю. Республиканская олимпиада, как образовательный процесс, позволяет выявить степень развития интеллектуального потенциала страны. Так, при оценивании деятельности отдельной школы выявляется «профессиональная компетенция педагогических кадров, индивидуальные достижения обучающихся, показатели общешкольных достижений в обеспечении качества образования» [1, с. 75]. В виды оценивания образовательных достижений учащихся, наряду с переводными и выпускными экзаменами, общереспубликанским тестированием, итоговой государственной аттестацией по математике, включены и математические олимпиады [2]. Таким образом, учитывая значение олимпиад в системе школьного образования, их роль в формировании интеллектуального ресурса государства, содержание статьи сконцентрировано на реальном состоянии подготовки школьников к математическим олимпиадам, их возможностях в формировании компетенций.
Цель исследования состоит в изучении и обобщении опыта организации и проведения республиканской олимпиады школьников Кыргызской Республики, включающего их подготовку в учреждениях дополнительного образования; в определении меры участия представителей администрации, общественных фондов, органов образования, вузов республики в олимпиадном движении Кыргызстана. Более пристальное внимание уделено олимпиадам по математике и предметам естественно-научного цикла в 2017 и 2018 гг.
Материалы и методы исследования
В ходе исследования применялись: анализ психолого-педагогической, методической литературы, программных документов по данной проблеме в области обучения математике, положения об олимпиаде, протоколов всех этапов республиканской олимпиады; изучение педагогического и методического опыта школ, вузов Кыргызской Республики по организации предметных олимпиад школьников, наблюдение за процессом их проведения; изучено содержание олимпиадных заданий по математике.
Результаты исследования и их обсуждение
В период времени 2010–2017 гг. являются актуальными исследования, посвящённые содержанию подготовки и проведения олимпиад, ее целям и функциям, вопросам создания базы данных олимпиадных задач, учебных материалов и методических разработок, на основе которых возможно усовершенствование организации олимпиад. Так, организационно-педагогические условия проведения олимпиад по математике освещались в [3], выявлены функции олимпиад [4], разработаны рекомендации по формированию исследовательских умений и навыков старшеклассников при подготовке к олимпиадам [5], к конкурсам научных работ, к проектам [6], исследовалась проблема формирования учебно-познавательной компетенции учащихся в условиях олимпиады по физике [7], по химии [8], по географии [9], поднимались вопросы развития компетентностей учащихся в системе дистанционных эвристических олимпиад [10], разработаны технические решения для проведения олимпиад по информатике и программированию [11].
Предметная олимпиада как образовательный процесс: «создает условия для выявления уровня сформированности знаний, умений и навыков учащихся» [9] и выполняет функции, содержание которых заключается в личностном развитии учащихся. Так, стимулирующую, обучающую, контролирующую и представительскую функции олимпиад Д.В. Подлесный дополняет адаптационной функцией [7]. В.И. Вышнепольский выявил 22 функции предметных олимпиад, объединив их в 6 групп: гуманистические, творческие, организационные, контролирующие, представительские, мотивирующие учебную деятельность [4]. Руководитель команды России на международной математической олимпиаде Н.Х. Агаханов придает большое значение формированию психологической готовности к решению нестандартных задач, считая ее основной целью подготовки школьников к олимпиадам [12].
В ряде статей обосновывается позиция авторов, что компетентностный подход возможно реализовать как при участии школьников в олимпиадах, так и при их обучении решению олимпиадных задач [13–16]. Так: «Современная математическая олимпиада, соответственно компетентностному подходу, призвана решать задачи: развивать математические компетенции; способствовать формированию социально-коммуникативной компетентности; стимулировать способности к математическому творчеству» [13].
В процессе подготовки к олимпиаде создаются благоприятные условия для формирования компетентностей: «Деятельностный характер обучения, ориентация процесса участия и подготовки к математическим олимпиадам на развитие самостоятельности и ответственности ученика за процесс подготовки и результаты олимпиадной деятельности, создание условий для приобретения опыта достижения цели создают предпосылки для приобретения учеником ключевых компетентностей в процессе математической олимпиадной подготовки» [14]. На основе уровней сформированности учебно-познавательной компетентности учащихся [17], разработанной в соответствии с типами ведущей деятельности, мы определили эмоционально-психологические, регулятивные, социальные, учебно-познавательные, творческие компетенции, компетенции совершенствования школьников, формируемые в процессе подготовки к математическим олимпиадам [15, с. 340]. Олимпиадная задача выступает как инструмент формирования умений «взаимодействовать в группе, работать с разными источниками информации» [14]. Изучение содержания олимпиадных задач по математике показало их соответствие «составу и логической структуре математической компетентности: компетентность, определенные умения, постановка задач на саморазвитие» [16], и, находя решение олимпиадной задачи, ученик демонстрирует «сформированность математических компетентностей третьего уровня» [16], владение вычислительной, аналитико-функциональной, наглядно-образной, статистико-вероятностной компетенциями. Кроме того, в критериях оценки олимпиадной деятельности школьников выделены исследовательские компетенции: «оценка собственных достижений; эрудиция ученика в области олимпиадной математики; защита результатов олимпиадной работы» [16].
Таким образом, становится очевидным, что математическая олимпиада формирует компетентностную образовательную среду, в которой наиболее полно проявляются уровни сформированности ключевых и предметных компетентностей ее участников.
Для достижения качественного результата в содержание системы подготовки школьников к математическим олимпиадам на основе компетентностного подхода к обучению, апробированной в школах республики, включены следующие компоненты:
1. При подготовке школьников к участию в олимпиадах практикуются две формы:
– систематическая подготовка в течение всего учебного года, включая базовую школьную и дополнительную, осуществляемую посредством кружков, школы олимпийского резерва и др.;
– периодическая интенсивная подготовка перед проведением олимпиад.
Средствами обучения остаются учебник по математике, сборники олимпиадных задач, задачные базы сетевых образовательных ресурсов, а также ИКТ.
2. Формирование готовности бакалавров педагогической специальности профиля подготовки «Математика» к олимпиадной деятельности с учащимися, осуществляется в процессе обучения дисциплине по выбору «Внеклассная работа по математике и методика решения олимпиадных задач» [18].
3. Необходимость повышения квалификации учителей по теории и практике олимпиадной математики подтверждают следующие факты. Так называемый «период полураспада компетентности» для педагога составляет 5–6 лет. Этот термин, как «особая единица измерения устаревания знаний специалиста», означает временной промежуток, в течение которого профессиональная компетентность снижается на 50 % по мере устаревания знаний, приобретенных при обучении в вузе [19, с. 7]. Результаты анкетирования 120 учителей математики из 18 школ четырех областей республики показали: «83 % анкетируемых учителей главным затруднением в подготовке школьников к участию в олимпиадах считают отсутствие психолого-педагогических и методических знаний и умений. Учителя критично оценивают свою компетентность в области олимпиадной математики: ни один из опрошенных педагогов не оценивает свой уровень олимпиадной подготовки высоким, 40 % считают его средним, 70 % – низким» [13]. На основе вышеизложенного, представим модель системы подготовки школьников к математическим олимпиадам на рис. 1:

Рис. 1. Компоненты системы подготовки школьников к математическим олимпиадам
Большую роль в развитии олимпиадного движения республики сыграло введение математической специализации отдельных школ в 1966 г., когда был издан приказ Министерства образования Кыргызской Республики об открытии одного 9-го и одного 5-го математических классов в школах № 61, № 9, № 5 г. Фрунзе (ныне г. Бишкек), в школе № 20 г. Ош [20, с. 217]. Это позволило в 1987 г. провести XXI Всесоюзную олимпиаду школьников СССР по математике в г. Фрунзе. Первая республиканская олимпиада в стране была проведена в 1967 г. по трем предметам: математика, физика, русский язык.
В современном Кыргызстане олимпиада, согласно положению [21]: «организуется ежегодно Министерством образования и науки вместе с Кыргызской академией образования, научно-педагогической общественностью, образовательными организациями, для учащихся школ, осваивающих базовое и углубленное изучение предмета. И традиционно проходит в четыре этапа, состав команды последующего этапа формируется из числа победителей предыдущих этапов:
I. Школьные олимпиады проводятся в ноябре. Участвуют все желающие учащиеся.
II. Региональные олимпиады проводятся в январе.
III. Городские (областные) олимпиады проводятся в январе и феврале, в два тура. Участвуют ученики 9-11 классов общеобразовательных и статусных школ (лицеи, гимназии).
IV. Республиканская олимпиада проводится в марте. Участвуют учащиеся 10–11 классов, занявшие I место на городской (областной) олимпиаде» [20, с. 215].
Задачи республиканской олимпиады формируются соответственно ГОС среднего общего образования КР [22] на основе принципов [23, с. 17]. Законом «Об образовании» КР закреплено право ее победителей на получение образовательных грантов для обучения в вузах республики.
Организация олимпиадной подготовки по математике в младших классах. В 1961 г. по распоряжению Совета Министров Кыргызской ССР в г. Фрунзе основана республиканская объединенная станция юных техников и натуралистов, создавшая постоянно действующую республиканскую выставку технического творчества школьников. В 1982 г. станция переименована в республиканскую детскую инженерно-техническую академию (РДИТА) «Алтын туйун», задачами которой являются выявление талантов и развитие творческого потенциала молодежи в сфере технологического образования. В академии работает свыше 25 направлений, 90 кружков [24]. В содержание кружковых занятий входят задачи нестандартного типа, задачи международного конкурса «Кенгуру».
Республиканская заочная математическая школа (РЗМШ), функционирующая в академии, ежегодно организует для учеников 3–8 классов республиканскую заочную математическую олимпиаду (РЗМО) «Юные Пифагоры в мире техники». В 2018 г. в олимпиаде пробовали силы и воспитанники казахстанского научно-практического образовательного центра «Бобек». На рис. 2 показаны результаты РЗМО 2017 г. и 2018 г.
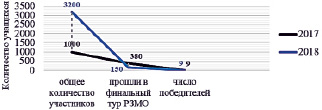
Рис. 2. Участие школьников в РЗМО в 2017 и 2018 гг.
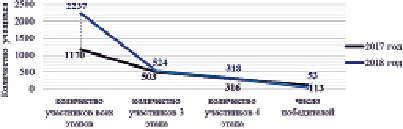
Рис. 3. Участие школьников в республиканской олимпиаде 2017 и 2018 гг.
Как видим из рис. 2, популярность РЗМО среди школьников в 2018 г. возросла, что дало возможность повысить требования к отбору участников в заключительный тур, тем самым способствуя формированию более качественного состава победителей олимпиады.
С целью выявления одаренных детей, развития их интереса к изучению математики, совершенствования различных видов интеллектуальных соревнований для учащихся республики и создания условий их дальнейшей поддержки, МОН КР проводит олимпиаду АКМО (математическая олимпиада для шестиклассников) среди учащихся 6-х классов общеобразовательных школ. Олимпиада проводится в три этапа по материалам образовательных программ 5–6 классов. В районном, областном этапах принимают участие по 5 учеников школ, гимназий, лицеев, призеров предыдущих этапов. В республиканском этапе участвуют областные и городские команды, состоящие из трех призеров 2 этапа.
Организация городского этапа олимпиады. В работе комиссии городского и республиканского этапов олимпиады школьников принимают участие представители профессорско-преподавательского состава высших учебных заведений, специалисты городских управлений образования и ведущие учителя школ республики. Так, одним из инициаторов проведения городской олимпиады и первой в СССР республиканской олимпиады по информатике является член-корреспондент НАН КР П.С. Панков. Его вклад в методику составления олимпиадных заданий по информатике заключается в следующем: «…сформулированы требования к компьютерному тестированию знаний: формируемость, уникальность и полная конфиденциальность заданий, разработана методика их реализации, введено понятие обязательно-коллективного тестирования знаний и интеллектуального глазомера, разработана методика составления олимпиадных заданий с использованием условий Кыргызстана» [25]. Сегодня профессор возглавляет жюри республиканской олимпиады и сборную Кыргызстана на международных олимпиадах по информатике.
К городскому этапу олимпиады допускаются ученики 9–11 классов, призеры предыдущих этапов. В г. Ош отборочный тур городской олимпиады проводится в тестовой форме в режиме офлайн на базе Ошского технологического университета.
Организация республиканского этапа олимпиады. К заключительному этапу олимпиады допускаются победители городского этапа среди 10–11 классов. Участие школьников в 3 и 4 этапах олимпиады в 2017 и 2018 гг. показано на рис. 3.
В 2017 г. республиканская олимпиада охватывала 10 школьных дисциплин, в 2018 г. – 12, следовательно, увеличилось и количество участников. В 2017 г. призёры республиканской олимпиады составили 9,7 % от числа участников всех этапов и 36 % от числа участников заключительного этапа, в 2018 г. это соотношение составило 2,4 % и 17 % соответственно. Разработка более точных критериев отбора победителей заключительного этапа олимпиады привела к уменьшению количества призовых мест более чем в два раза. На рис. 4 показано распределение призовых мест олимпиад по регионам республики:
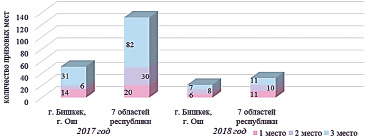
Рис. 4. Распределение призовых мест республиканской олимпиады 2017 г., 2018 г. по регионам
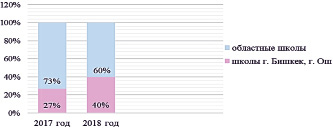
Рис. 5. Доля призеров олимпиады в городских и областных школах республики
Из рис. 5 видно, что в 2018 г. соотношение доли призеров из школ северной и южной столиц республики и призеров из областных школ изменилось на 13 %:
В числе победителей олимпиады – ученики гимназий с углубленной математической подготовкой, воспитанники лицеев международного образовательного учреждения «Сапат», реализующего программу «Одаренные дети», а также школы, в процесс обучения которых в 2015–2018 гг. была внедрена программа школы олимпийского резерва по математике.
Изучив опыт организации олимпиад в соседних республиках, мы выявили, что олимпиады в Казахстане и Российской Федерации также проводятся в четыре этапа: школьная, районная (городская в областных центрах), областная (городская) и республиканская. Однако, в отличие от олимпиады КР, на заключительный этап отбираются 2 лучшие работы по итогам областных олимпиад [26, с. 104]. Российские школьники успешно принимают участие в «более чем 160 различных видов олимпиад по математике» [27], среди которых есть «узконаправленные геометрические олимпиады» [28]. «Основной причиной организации олимпиад по геометрии для школьников стало желание учителей математики остановить процесс облегчения геометрического, а как следствие, и математического образования в стране» считают авторы [29, с. 19]. Хотя в задания республиканских олимпиад обязательно включена одна задача по геометрии, но для стимуляции интереса школьников к изучению предмета можно перенять этот опыт, организовав свои геометрические олимпиады.
Участие школьников в международных олимпиадах. Победители республиканской олимпиады входят в состав сборной, представляющей Кыргызстан в ряде престижных международных олимпиад по различным предметам, табл. 1.
Таблица 1
Участие Кыргызстана в международных олимпиадах
|
Год |
Международные олимпиады |
Место проведения |
Кол-во стран-участниц |
Награды кыргызстанцев |
|
2010 |
LI математическая олимпиада |
г. Астана, Казахстан |
97 стран |
1 серебряная, 2 бронзовые медали, 3 почетные грамоты |
|
2010 |
DCXLII олимпиада по химии |
г. Токио, Япония |
68 стран |
дипломы |
|
2010 |
XLIV Менделеевская олимпиада по химии |
г. Баку, Азербайджан |
14 стран |
серебряная медаль |
|
2010 |
XLI олимпиада по физике |
г. Загреб, Хорватия |
82 страны |
4 место, грамоты |
|
2015 |
XII естественнонаучная олимпиада школьников |
г. Тэгу, Южная Корея |
43 страны |
бронзовая медаль |
|
2016 |
L менделеевская олимпиада по химии |
г. Москва, Россия |
21 страна |
бронзовая медаль |
|
2016 |
XLVII олимпиада по физике |
г. Цюрих, Швейцария |
90 стран |
бронзовая медаль |
|
2016 |
LII олимпиада по биологии |
г. Ханой, Вьетнам |
72 страны |
бронзовая медаль |
|
2017 |
XXIX Азиатско-Тихоокеанская математическая олимпиада |
Алматы, Казахстан |
41 страна |
2 бронзовые медали |
|
2017 |
II Международная олимпиада мегаполисов |
г. Москва, Россия |
18 стран |
4 бронзовые медали: 1 по математике, 1 по информатике, 2 по физике |
|
2018 |
XLIX Международная олимпиада по физике |
г. Лиссабон, Португалия |
87 стран |
2 бронзовые медали, 2 грамоты |
|
2018 |
Международная олимпиада по физике и астрономии |
г. Самарканд, Узбекистан |
4 страны |
золотая медаль |
|
2018 |
III Международная олимпиада мегаполисов |
г. Москва, Россия |
19 стран |
4 бронзовые медали: 2 по информатике, 2 по физике |
|
2018 |
Евразийская олимпиада по программированию |
г. Алматы, Казахстан |
4 страны |
3 бронзовые медали |
|
2018 |
Международная олимпиада «Лаборатория подготовки талантов» (предметы: математика, физика, химия) |
г. Баку, Азербайджан |
10 стран |
бронзовая медаль |
Школьники активно участвуют в математических олимпиадах с очным и заочным участием, использующих возможности дистанционных технологий: «Сегодня в Кыргызстане проводится ряд олимпиад, требующих от школьников сформированной ИКТ-компетентности» [14]. В своем интервью Н.Х. Агаханов указывал на необходимость подготовки с учетом сложности международных олимпиад: «Во многих странах мира в школах в большем объеме, чем у нас, изучаются некоторые разделы алгебры, теории чисел, математического анализа. Это оказывает влияние на содержание заданий заключительных этапов нашей олимпиады, и это нельзя не учитывать при подготовке к олимпиадам» [12]. Поэтому к систематической подготовке олимпийской сборной привлекаются преподаватели вузов и студенты, имеющие позитивный опыт участия в международных олимпиадах.
Помимо предметных олимпиад, в республике проводятся и другие интеллектуальные соревнования, конкурсы. Так, международная игра-конкурс «Кенгуру. Математика для всех» проводится в Кыргызстане с 2005 г. [26, с. 104]. В 2010 г. в конкурсе приняли участие 1700 учеников 2–11 классов из двадцати школ городов Бишкек, Каракол, Балыкчы. Однако с появлением национальных олимпиад АКМО, Билимкана, РЗМО «Юные Пифагоры в мире техники» эта игра утратила свою популярность среди наших школьников.
Ученики 9–11 классов Бишкека соревновались в знаниях и практических навыках в области геологии в X и XI Всероссийской открытой полевой олимпиаде юных геологов 2016 г. и 2017 г. в г. Кемерово, заняв 5-е место в 2016 г. В олимпиаде участвовали более 30 команд из России, Беларуси, Казахстана, Кыргызстана, Узбекистана и Таджикистана.
В 2017 г., вместе с учащимися Армении и Казахстана, кыргызстанские школьники приняли участие в олимпиадах Национального исследовательского ядерного университета «МИФИ» – «Росатом» и инженерной олимпиаде, целью которых было заинтересовать школьников инженерными специальностями [30, с. 127–128].
Воспитанники академии «Алтын туйун» ежегодно представляют свои работы на городских, зональных, республиканских, международных выставках технического творчества. Так, в Бишкеке проводятся соревнования роботов для учеников лицеев и начальных школ. Следствием деятельности академии являются достижения ее учеников на международной олимпиаде юных изобретателей 2016 г. в г. Пенанг (Малайзия), в которой приняли участие 12 стран мира, представившие 216 проектов. Сборная Кыргызстана представила 24 проекта, выиграв 5 золотых, 6 серебряных и 13 бронзовых медалей.
В декабре 2017 г. проведена первая республиканская олимпиада по ментальной арифметике среди школ ISMA (Международная школа ментальной арифметики), в которой приняли участие 370 детей от 5 до 16 лет из 5 городов республики. В 2017 и 2018 гг. школьники принимали участие в международных олимпиадах (табл. 2).
Таблица 2
Результаты международной олимпиады по ментальной арифметике
|
Год |
Олимпиада |
Город |
Кол-во стран-участниц |
Количество медалей |
|
2017 |
Международная олимпиада по ментальной арифметике |
г. Алматы |
6 стран |
47 золотых, 39 серебряных, 30 бронзовых медалей |
|
2018 |
г. Дубаи |
12 стран |
12 золотых, 19 серебряных, 14 бронзовых медалей |
Влияние результатов олимпиад на результаты общереспубликанского тестирования (ОРТ). В структуру основного теста ОРТ включены: математика, словесно-логический тест, практическая грамматика родного языка. Содержание заданий позволяет оценить компетентность учеников по 6 уровням таксономии Б. Блума: знание, понимание, применение, анализ, синтез, оценка – т.е. охватывает все стадии познавательного процесса.
Для поступления в вузы определены пороговые 110 баллов, максимальный балл по шкале ОРТ составляет 250 баллов. На рис. 6 показаны лучшие результаты ОРТ 2017, 2018 гг.
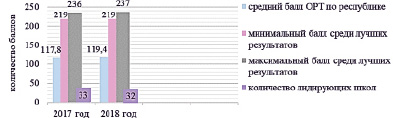
Рис. 6. Лучшие результаты школьников в ОРТ в 2017 и 2018 гг.
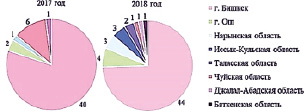
Рис. 7. Распределение количества «золотых сертификатов» ОРТ по регионам республики
Участники тестирования, получившие высшие баллы от 219 до 250, становятся обладателями так называемых «золотых сертификатов» с правом поступления на бюджетное отделение в любой вуз страны. В 2017 г. выпускники 32 школ, в 2018 г. – 33 школ (около 1,5 % всех школ республики) награждены «золотыми сертификатами» за лучшие результаты ОРТ. На рис. 7 показано количество «золотых сертификатов» в регионах.
Как видим из рис. 6, 7, в 2017 г. 80 % «золотых сертификатов» получили выпускники столичных школ, в 2018 г. их доля составила 75 %. Доля «золотых сертификатов» выпускников школ из областей республики составила в 2017 г. 20 %, в 2018 г. 25 %. Их ряды пополнили школьники Иссык-Кульской и Таласской областей, показав результаты 221–224 баллов. Как правило, это школы с углубленным изучением дисциплин, в которых ведется целенаправленная олимпиадная подготовка и имеются другие возможности для получения дополнительного математического образования.
Руководители городских и районных отделов образования объясняют низкий уровень школьных знаний дефицитом кадров, как одной из главных проблем. Другой на наш взгляд, основной причиной, являются негативные последствия сокращения количества учебных часов по математике в общеобразовательных школах до 4 часов в неделю, по алгебре, алгебре и началам анализа до 3 часов, по геометрии до 1 часа в неделю. Школьным компонентом учебного плана, предусмотрено по 1 часу для каждого из этих предметов, однако этого недостаточно для качественного усвоения математического материала. В результате выпускники школ, не получая достаточных знаний на уроках, не осваивают олимпиадную программу, основанную на высоком уровне базового школьного образования по математике. В школах-гимназиях и лицеях ситуацию спасает дополнительное образование. Так, гимназическим компонентом предусмотрено 2 часа в неделю для проведения кружковой работы и 2 часа в неделю для занятий олимпийского резерва школы.
Школьные учителя считают необходимой подготовку детей с младшего школьного возраста: «При подготовке учеников к олимпиадам потребность в расширенном изучении предмета математики возникает уже с 5 класса» [13]. И акцентируют внимание, что действующие учебники не отвечают программе олимпиад, хотя эффективная подготовка: «требует от учителя выхода за рамки школьной программы и демонстрации новых методов решения» [23, с. 22]. Принимая это во внимание, в обязательную школьную программу по математике для 5–9 классов с 2016 г. включены элементы логики, комбинаторики, статистики и теории вероятностей.
Участие вузов, общественных организаций и фондов в олимпиадном движении республики. С целью популяризации специальностей физико-математического профиля и приобщения талантливых учащихся к науке вузы республики ежегодно проводят олимпиады для школьников, выполняющие: «профориентационную, квалификационную, мотивационную функции» [30]. Так, Американский университет в Центральной Азии (АУЦА) проводит ежегодную олимпиаду по математике для старшеклассников Кыргызстана с 2012 г. Задания олимпиады состоят из авторских задач, разработанных доцентами АУЦА.
С 2014 г. для учащихся 8–11 классов, Московский физико-технический институт в партнерстве с физико-математическим лицеем № 61 г. Бишкек, проводит ежегодную физико-математическую олимпиаду «Иссык-Куль» с участием членов жюри Всероссийских олимпиад [20, с. 217]. Олимпиада организуется при поддержке Российского центра науки и культуры. Ошский государственный университет ежегодно проводит олимпиаду по естественнонаучным дисциплинам для учащихся 9–11 классов [20, с. 215]. Кроме того, в рамках проекта «Проведение тренингов для работников образования КР», университетом были организованы курсы повышения квалификации, на которых 83 учителя математики юга республики прошли десятичасовой курс обучения по методам решения олимпиадных задач.
В 2017 г. Кыргызско-Российский Славянский университет совместно с Кыргызской ассоциацией разработчиков программного обеспечения и услуг провели первую олимпиаду по программированию для школьников «IT кубок Кыргызстана».
Свой вклад в развитие интеллектуального ресурса страны вносят и общественные фонды «Билимкана» и «Аракет», выступая организаторами национальных олимпиад для школьников 4–11 классов. Партнерами олимпиады Билимкана, в которой предусмотрены базовый (Science) и углубленный (Advanced Math) уровни для учащихся с соответствующей программой обучения по математике, выступают национальный исследовательский университет «Высшая школа экономики» г. Москвы и АУЦА.
Введение инноваций в процесс организации олимпиад. Для поэтапного искоренения коррупции на государственных олимпиадах приняты меры, обеспечивающие доступность и открытость их проведения. Так, по приказу МОН КР 2015 г. II тур олимпиады на территории г. Ош проводится в пилотном режиме в формате офлайн. Мгновенные результаты олимпиады могут наблюдать и ученики за компьютером, и их родители на таблоиде в зале ожидания. С 2016 г. ученики проходят видеорегистрацию, что позволяет уменьшить спорные вопросы после олимпиады [20, с. 215]. С 2017 г. заключительный этап олимпиады транслируется в онлайн-режиме на сайте live.manas.edu.kg, на канале YouTube. В 2018 г. для разработки олимпиадных заданий III и IV этапов олимпиады на конкурсной основе впервые привлечена независимая организация «Центр оценки в образовании и методов обучения», специализирующаяся на научно обоснованном, независимом тестировании в Кыргызстане. Несмотря на то, что в практике проведения международных олимпиад ежегодно меняются место проведения, комиссии, организации, участвующие в олимпиадах, в Кыргызстане состав комиссий практически не меняется. Это одна из причин, по которой учителя не удовлетворены результатами олимпиад, считая их фальсифицированными. Поэтому предлагаем дополнить антикоррупционные меры по организации олимпиады:
1. К заключительному этапу республиканской олимпиады должны быть допущены дети, занявшие первые три места на городских олимпиадах.
2. В состав предметных комиссий 3 и 4 этапов включить преподавателей из трех вузов из разных регионов республики.
3. В аудитории, где заседает комиссия, должны находиться не менее трёх независимых наблюдателей: преподавателей вузов, не специалистов по данному предмету; педагогов школ, в том числе и школ, участвующих в олимпиаде по данному предмету.
4. Независимым наблюдателям запрещено вмешиваться в ход проверки олимпиадных работ и апелляции и разрешено составлять акты и замечания для их рассмотрения в МОН КР.
5. В аудитории, где проходит предметная олимпиада, должны находиться наблюдатели – педагоги разных школ, специализирующиеся по данному предмету, исключая учителей самой школы, на базе которой проходит олимпиада.
6. Олимпиадные работы и их копии необходимо сканировать, копии запломбировать в присутствии независимых наблюдателей, заверить печатями до проверки. В течение апелляции, независимые наблюдатели, кураторы, участники имеют право сверить копию и оригинал для устранения возможности подтасовки.
7. По окончанию олимпиады ксерокопии работ участников, занявших I–V места должны быть вывешены в общем зале вместе с правильными решениями заданий.
Заключение
Математические олимпиады, создавая компетентностную образовательную среду, относятся к числу факторов, влияющих на развитие ключевых и предметных компетентностей, формирование которых необходимо в системе среднего общего образования Кыргызской Республики.
Деятельность детских развивающих центров, лицеев, заочных математических школ, физико-математических лагерей, школы олимпийского резерва имеет большой потенциал в подготовке школьников к олимпиадам всех уровней.
Совместная работа учителей математики, работников управления образованием, вузов, общественных фондов республики положительно влияет на формирование мотивации учащихся к участию в математических олимпиадах.
Необходимо приблизить олимпиады к международным нормам, изменив правила проведения, соблюдая антикоррупционные меры в их организации, сделав упор на доступность и открытость, разработать программу олимпиадной математики, соответствующую уровню международных математических олимпиад.
Выражаем свою благодарность коллективам школ республики, вузам г. Ош за предоставление экспериментальной площадки и материалов исследования.



