В современной научной литературе научная школа рассматривается как важнейший элемент академической структуры науки, как источник новых идей и новых технологий, как один из главных факторов развития экономики и общества в целом, как источник подготовки научных кадров нового поколения [1–4]. Многие исследователи концентрируют основное внимание либо на истории возникновения научной школы и на основные результаты мирового уровня, полученные в ней, либо на особенности руководства и деятельности самого лидера научной школы, либо на особенности функций и характеристик научного коллектива в конкретной области знаний и т.д. Но вся эта информация большей частью носит описательный характер в форме воспоминаний или описаний и анализа научных результатов. Но на вопрос, как в творческом коллективе получаются выдающиеся результаты, ответ не дают. Эту сложную задачу впервые пытался решить доктор физико-математических наук И.Д. Сафронов, в свое время возглавлявший математическое отделение Российского федерального ядерного центра (РФЯЦ) – ВНИИ экспериментальной физики (г. Саров) [5]. На основе чисел и структур он разработал математические модели деятельности научного коллектива, предложил несколько архитектур научного коллектива, а также принципы распределения приоритета в моделях коллективного творчества. В работе [6] предлагается когнитивная модель деятельности научно-исследовательского отдела (НИО), построенная на основе информации, полученной в ходе социальных исследований реального научно-производственного предприятия. По модели было получено множество параметров, характеризующих состояние предприятия, и множество целевых переменных, характеризующих результативность его работы. В работе [7] нечеткие когнитивные модели НИО используются для выработки управленческих решений с целью повышения производительности и результативности работы НИО. Рассматривалось влияние четырнадцати взаимосвязанных факторов на эффективность деятельности отдела. Проблема управления научной школой как организационной системой рассматривается в работе Д.А. Новикова [8], а управление научной школой как динамической многосвязной системой – в работе авторов [9].
Цель исследования: анализ устойчивости процессов управления деятельностью научной школы как многосвязным динамическим объектом; разработка математической модели многосвязной системы управления деятельностью научной школы, критерия для оценки устойчивости многосвязной системы.
Понятие научной школы как многосвязного динамического объекта управления
Авторы в дальнейшем придерживаются следующего понятия: «Научная школа – это интеллектуальная, эмоционально-ценностная, неформальная, открытая общность (структура, объединение) ученых разных статусов, разных уровней знаний, разрабатывающих под руководством лидера, выдвинутую им научно-исследовательскую программу» [10]. Это определение в большей степени подходит к оценке научной школы (НШ) как многомерного объекта управления. Выделим три основные цели, которые должны быть достигнуты при функционировании НШ:
– коллективное выполнение поставленной научно-исследовательской проблемы или сложного проекта;
– подготовка научных кадров и специалистов для решения проблемы или выполнения проекта;
– разработка и защита научных идей в форме патентов, статей, докладов, монографий.
Для управления такой НШ как сложным динамическим объектом требуется высокий уровень самоорганизации всего коллектива в виде трех взаимосвязанных подсистем, каждая из которых стремится достичь своей цели на заданном отрезке времени и пространства. Особенность такой организации заключается в том, что каждый член коллектива участвует в функционировании всех трех подсистем, выполняя возложенную на нее функцию, при этом передавая свои знания коллегам, никак не уменьшая собственный запас знаний. При такой организации управления возможно появление человеческих факторов в форме запаздывания во времени выполнения возложенной функции или принятия решений, некачественного выполнения функций, что приведет к снижению коэффициента вклада того или иного члена коллектива в результативность деятельности всего коллектива. Учитывая такую неопределенность и нестабильность изменения параметров многосвязной организационной системы управления НШ, можно с уверенностью утверждать, что проблема устойчивости становится одной из основных научных проблем управления. Эту проблему далее будем рассматривать на уровне математической модели многосвязной системы управления (МСУ) деятельностью НШ.
Математическая модель многосвязной системы управления деятельностью научной школы
Структура модели линейной многосвязной системы управления деятельностью научной школы представлена на рис. 1.
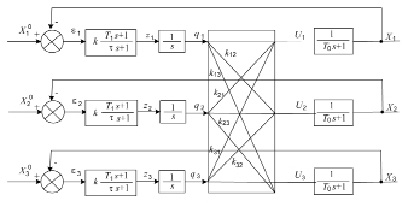
Рис. 1. Трехсвязная система управления научной школой
Рис. 2. Структура системы управления НШ в векторно-матричной форме
При разработке модели были сделаны следующие допущения:
– единица времени (1 с) может быть эквивалентной другим физическим единицам времени (час, сутки, месяц, год и т.д.) в зависимости от содержания решаемой задачи;
– отрезок времени устойчивого функционирования системы также должен соответствовать реальному физическому отрезку времени, на котором достигаются цели;
– численные значения цели, равные 1, или 100 %, для каждой реализуемой выходной координаты соответствуют тому объему работ, который должен быть выполнен соответствующей подсистемой на заданном отрезке времени.
Значения переменных на рис. 1 имеют следующий смысл:
– xi(t), xi0(t) – регулируемые и целевые переменные, при этом x1(t) соответствует объему работ по выполнению проекта, x2(t) – объему работ по подготовке специалистов, научных кадров и по повышению уровня их знаний; x3(t) – объему работ по документализации полученных знаний, в виде статей, докладов, монографий, технических и проектных отчетов, методик, технологий;
– εi(t) = xi0(t) – xi(t) величина рассогласования (ошибки) между целевыми и текущими значениями i-й переменной;
– zi(t) – переменная, характеризующая результат принятия управленческого решения;
– qi(t) – переменная, характеризующая интегральное значение результата принятых управленческих решений;
– Ui(t) – входная координата (управление) на динамический объект, выходной координатой которой является переменная xi(t).
Далее делается предположение (для облегчения расчетов), что все подсистемы идентичны (однотипны по математической модели) и динамические параметры подсистем соответственно одинаковы. Значения параметров подсистемы (рис. 1) имеют следующий смысл:
– параметр k – обобщенный коэффициент передачи всей разомкнутой подсистемы, определяющий ее динамические свойства (в реальной системе он распределен между элементами подсистем);
– параметр τ – динамическое запаздывание, связанное с инерционностью принятия решения по обработке скорости изменения переменной ε;
– параметр T1 характеризует величину скорости по ошибке ε?(t), участвующей в принятии управленческого решения;
– параметр T0 – характеризует инерционность выполнения работ по соответствующим координатам.
Отметим, что связь между подсистемами осуществляется по переменным qi, когда каждая из переменных qi участвует в формировании переменных управления Ui со своим коэффициентом kij влияния.
Представим структуру многосвязной системы (рис. 2) в векторно-матричной форме.
Здесь X0(s), X(s) – векторы целевых и выходных переменных, E(s) – вектор ошибок, Z(t) – вектор управленческих решений, Q(s) = {qi(s)} – вектор интегральных значений принятых управленческих решений, H – числовая матрица, определяющая значение вектора управления Ui(s) как линейную сумму векторов qij: Ui(s) = Σqij, с соответствующими коэффициентами kij,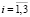 
. В рассматриваемой структуре матрица R(s) диагональная матрица: R(s) = diag{ri(s)}, где ri(s) = k(T1s + 1)/(τs + 1); матрица J(s) – диагональная матрица: J(s) = diag{1/s}, W0(s) – диагональная матрица объектов управления: W0(s) = diag{1/(T0s + 1)}. Числовая матрица H связей равна
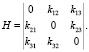(1)
Характеристическое уравнение многосвязной системы управления научной школой
Основываясь на работе [11], запишем характеристическое уравнение трехсвязной системы через индивидуальные характеристики идентичных подсистем и групповые числовые коэффициенты (hi) связей между ними:
D(Φ, h) = 1 + h2Φ2(s) + h3Φ3(s) = 0, (2)
где Φ(s) – передаточная функция автономной подсистемы в режиме управления, равная
Φ(s) = W(s)/1 + W(s), (3)
где W(s) – передаточная функция разомкнутой подсистемы;
h2 – сумма произведений всех пар коэффициентов детерминанта матрицы H связей;
h3 – сумма произведений всех троек коэффициентов детерминанта матрицы H связей.
Далее подставив (3) в (2), представим характеристическое уравнение (2) трехсвязной системы через передаточные функции W(s) разомкнутой подсистемы:
D(W, h) = (1 + h2 + h3)W3(s) +
+ (3 + h2)W2(s) + 3W(s) + 1 = 0. (4)
Условие 1 + h2 + h3 > 0 выражает статистическую устойчивость системы. Оно получается также из уравнения (2) при условии, что Φ(0) = 1.
Теперь перейдем от передаточной функции W(s) к частотной характеристике W(jω), подставив в (4) s = jω:
D(W(jω),h) = (1 + h2 + h3)W3(jω) +
+(3 + h2)W2(jω) + 3W(jω) + 1 = 0, (5)
получим характеристическое уравнение многосвязной системы в частотной форме.
Критерий устойчивости многосвязной системы
Далее рассмотрим задачу: как, не решая уравнение (5), можно судить об устойчивости трехсвязной системы (2) по поведению амплитудно-фазовой характеристики (АФХ) W(jω) разомкнутой подсистемы?
Для решения задачи необходимо найти значения критических точек, которые лежат на мнимой оси трехсвязной системы. Этими критическими точками будут корни уравнения связи, образованного заменой АФХ W(jω) на переменную x:
D(x, h) = (1 + h2 + h3) x3 +
+ (3 + h2) x2 + 3x + 1 = 0. (6)
Пусть множество корней {x1,x2,x3} уравнения (6) при заданных числовых коэффициентах (h2,h3) связи и будут составлять критические точки на комплексной плоскости W(jω). Отсюда можно сформулировать модернизированный критерий устойчивости многосвязной системы.
Критерий устойчивости. Для устойчивости многосвязной системы с однотипными (идентичными) подсистемами и числовыми связями между ними необходимо и достаточно, чтобы АФХ W(jω) разомкнутой подсистемы при изменении ω от 0 до + ∞ не охватывала бы критические точки уравнения связи (6). Результаты анализа устойчивости многосвязной системы (2) по данному критерию и по критерию, изложенному в статье [11], совпадают, так как оба они основаны на необходимом и достаточном условии устойчивости линейных динамических систем. Данный критерий можно рассматривать как модернизированный критерий устойчивости многосвязной системы по АФХ W(jω) разомкнутой подсистемы. Однако данная форма критерия устойчивости обладает рядом преимуществ, которые позволяют быстрее определять такие критические параметры, как критический коэффициент передачи разомкнутой подсистемы, критическое значение динамического и чистого запаздывания, критическое значение инерционности и коэффициента демпфирования объекта управления.
Пример: рассмотрим трехсвязную систему управления научной школой (рис. 1). Передаточная функция W(s) разомкнутой подсистемы равна: W(s) = k(T1s + 1)/s(τs + 1)(T0s + 1), где числовые значения параметров соответственно равны: T1 = 0, τ = 0,5 c, T0 = 1 c. Требуется определить критическое значение коэффициента k при заданных коэффициентах kij матрицы связи, числовые значения которых равны друг другу и равны 0,5.
Тогда определим числовые значения коэффициентов связи: h2 = –3·0,52 = –0,75, h3 = 2·0,53 = 0,25. Условие статической устойчивости: 1 + h2 + h3 > 0 выполняется.
Составим в числовом виде уравнение критических точек в соответствии с уравнением (6):
D(x) = 0,5x3 + 2,25x2 + 3x + 1.
Корни уравнения, т.е. множество критических точек, равно: x1 = –0,5, x2 = –2, x3 = –2. Ближайшей критической точкой x? будет корень x1 = –0,5 (рис. 3).
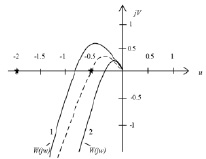
Рис. 3. АФХ W(jω)
Из рисунка видно, что АФХ-1 соответствует устойчивой подсистеме в автономном режиме, т.е. при отсутствии связей kij, и соответствует неустойчивой трехсвязной системе, так как охватывает критическую точку x1 = -0,5. А АФХ-2 соответствует устойчивой многосвязной системе. Далее определим критическое значение коэффициента k подсистемы. Для этого, подставив в W(s) s = jω, выделим вещественную и мнимую части: W(jω) = U(ω) + jV(ω),где, U(ω) = –k(τ + T0)/(1 + τ2ω2)(1 + T02ω2),V = –k(1-τT0ω2)/ω(1 + τ2ω2)(1 + T02ω2). Отсюда видно, что ω2 = 1/τT0, U(ω) должна быть меньше x?.
Тогда получаем:
k < x?(1/τ+ 1/T0). (7)
Для автономной подсистемы, а для многосвязной системы x? = –0,5 и k < 5,5.
Из формулы (7) видно, что с увеличением инерционности, как объекта управления, так и принятие решения значение критического коэффициента k в многосвязной системе падает. Например, при τ = 0,2 с и T = 5 с величина k не должна превышать в нашем примере величины 2,6. При уменьшении коэффициентов связи kij, например, до 0,2 критическое значение коэффициента k многосвязной системы растет и k < 9. При T0 > T1 > 0 запасы устойчивости системы увеличиваются.
Заключение
Предложена математическая модель многосвязной системы управления деятельностью научной школы. Предложен новый критерий устойчивости многосвязной системы управления, который позволяет на уровне математической модели по АФХ разомкнутой подсистемы оценивать устойчивость многосвязной системы в целом. Данный критерий предложено использовать для оценки устойчивости многосвязной системы управления деятельностью научной школы.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (18-08-00638).