Расчет критической скорости гидротранспортирования, так же как и удельных потерь напора, является важнейшим показателем, определяющим техническую возможность реализации и экономическую эффективность трубопроводного гидротранспорта твердых материалов. Анализируемый процесс необходимо учитывать при расчете трубчатых аппаратов в различных химических технологиях в которых используются гидромеханические процессы переноса частиц твердых веществ в жидкости. В отечественной технической литературе большая часть исследователей под критической скоростью понимают величину, которая определяется путем визуального наблюдения за потоком гидросмеси через специальные прозрачные вставки, установленные вдоль нижней образующей трубопровода, а опытное значение критической скорости определялось как минимальное значение скорости, при которой твердые частицы начинали выпадать на дно трубопровода [1].
Анализ методов расчетов критической скорости
В работах [2, 3] на основе собственных экспериментальных исследований и анализа практически всех известных эмпирических зависимостей иностранных авторов, предложено выражение для критической скорости гидротранспортирования монодисперсных частиц
Ucr = 0,124 α1/2[des (ρh/ρ) (gD)1/2/ν]0,37(des S/D)-0,007exp(3,1φ), (1)
где α = (ρp/ρ – 1) – относительная избыточная плотность гидросмеси; des – эффективный средний диаметр частиц по Саутеру (Sauter mean diameter), который равен отношению шестикратного объема частицы к площади её боковой поверхности; ρh = ρ(1 – φ) + ρpφ – плотность гидросмеси; ν – кинематическая вязкость жидкости; S – коэффициент сферичности частицы; φm – суммарная объемная доля твердой фазы; D – внутренний диаметр трубы; ρp – плотность материала частиц; ρ – плотность жидкости; φ – объемная доля твердой фазы
Критическую скорость гидротранспортирования для полидисперсных смесей твердых частиц в стальных трубопроводах, находящихся в длительной эксплуатации, рекомендуется определять по формуле, приведенной в работе [1]
Ucr = 9(αgDν/ ks)1/3(φ ψ)1/6, (2)
здесь ks – величина шероховатости стенки трубы; ψ – коэффициент фиктивного лобового сопротивления полидисперсной смеси частиц твердой фазы или коэффициент транспортабельности гидросмеси, который определяется по формуле
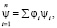 (3)
(3)
где φi – объемная доля частиц со средним диаметром частиц di; ψi – коэффициент фиктивного лобового сопротивления или коэффициент транспортабельности частиц со средним диаметром di, который определяется по табличным данным, приведенным в работе [1].
Выражение (2) основывается на обобщении опытных данных по гидротранспортированию полидисперсных смесей угля, песка и хвостов обогащения при изменении плотности твердой фазы от 1630 кг/м3 до 3360 кг/м3 [1].
На основании проведенных поверочных численных расчетов в дальнейшем принято, что значения коэффициентов транспортабельности определяются следующими непрерывными зависимостями [4], сглаживающими скачки коэффициентов ψi при табличном задании величин d,i в следующем виде
ψi = 0,02; при di ≤ 0,05 мм;
?g ψi = [–0,855247sin xi + 3,59186 cos xi – 4,02226]; (41)
при 0,05 мм ≤ di ≤ 0,375 мм;
?gψi = [0,0269317xi4 – 0,00195969xi3 – 0,387418xi2 + 0,690757xi – 0,0337382]; (42)
при 0,375 мм ≤ di ≤ 60 мм;
где xi = ?g di, причем размерность di в мм.
Проанализируем возможности использования эмпирических зависимостей (1) и (2) при определении критических скоростей частиц существенно более мелких фракций. Разные авторы определяют это понятие различным образом. Например, в работе [5] под частицами «пылевидных фракций» понимаются мельчайшие частицы, размер которых не превышает dd ≤ 10 мкм. Далее высказывается предположение, что эти частицы образуют несущую среду, со своей плотностью и вязкостью, в которой перемещаются частицы более крупных фракций из дисперсных частиц песка, хвостов обогащения или рудных концентратов. Какая-либо зависимость максимального размера мельчайших частиц от плотности материала частиц твердой фазы не предполагается, хотя физически ясно, что с повышением плотности материала частиц, их «избыточный» вес возрастает. В работе [6], при расчете параметров гидротранспортирования разработанных грунтов и нерудных полезных ископаемых учет влияния частиц мельчайших фракций не проводится. При расчете же параметров гидротранспортирования продуктов обогащения рудных полезных ископаемых, имеющих более высокую плотность материала частиц, рекомендуется к мелким частицам относить частицы
dd ≤ {6 M /[π (ρp – ρ)]}1/3, (5)
где М = 10-6г – средневзвешенная масса мелких частиц.
В работе [7] предполагается, что частицы крупностью менее 0,15 мм полностью увлекаются потоком и за счет этого повышают плотность несущей среды. Связанное с этим изменение вязкости несущей среды не обсуждается.
Цель работы: количественное уточнение понятия термина «частицы мельчайших фракций» двухфазной смеси, его физическое обоснование и уточнение эмпирической формулы для определения критической скорости при наличии частиц мельчайших фракций.
Уточнение понятия о мельчайших частицах твердой фазы
В работе [8] отмечается, что минимальный размер твердых частиц, для которых реализуется свободное осаждение твердых частиц, определяется из условия, что кинетическая энергия осаждающихся частиц равна средней кинетической энергии теплового движения молекул несущей жидкости. В случае частиц меньшего размера на процесс осаждения будет оказывать влияние броуновское движение молекул несущей жидкости, которое не учитывается ни в одном из известных методов расчетов движения двухфазных потоков. Принимая, что режим обтекания частиц ламинарный из условия равенства кинетической энергии осаждающейся частицы, определенной по скорости свободного осаждения при ламинарном режиме обтекания (cтоксовский режим гидравлического сопротивления) и тепловой энергии молекул жидкости, равной 3kT/2, получим
dd ≤ {5832 k T ν2 /[π (ρp/ ρ – 1)3g2 ρ]1/7}, (6)
где k = 1,38*10-23 Дж/К – постоянна Больцмана; T = 293 К – температура жидкости.
В табл. 1 приведены значения диаметров твердых частиц, рассчитанных по формулам (5) и при знаке равенства в (6). В расчетах принималось, что ρ = 103 кг/м3; ν = 10-6 м2/с.
Таблица 1
Максимальные значения диаметра твердых частиц dd, рассчитанных по зависимостям (5) и (6)
|
ρp, кг/м3; |
1500 |
2000 |
2500 |
3000 |
3500 |
4500 |
5500 |
6500 |
7500 |
8500 |
9500 |
|
dd , мкм (5) |
156 |
124 |
108 |
98 |
91 |
82 |
75 |
70 |
66 |
63 |
59 |
|
dd , мкм (6) |
18 |
13,4 |
11,3 |
9,96 |
9,06 |
7,8 |
7,0 |
6,5 |
6 |
5,7 |
5,4 |
Расчет величин dd по формулам (5) и (6) приводит к существенно разным значениям. Качественно это можно объяснить тем, что формула (5) получена в результате анализа опытных данных, полученных на продуктах обогащения рудных полезных ископаемых с большой плотностью материала твердых частиц, порядка 5000÷6000 кг/м3. В работе [5] к частицам пылевидных фракций относятся частицы менее 10 мкм, которые при плотности частиц твердой фазы порядка 2500÷3000 кг/м3 достаточно хорошо коррелируют с расчетом по формуле (6). По этой причине примем гипотезу, что именно пылевидные частицы вместе с жидкостью образуют однородную жидкую несущую среду, в которой перемещаются частицы более крупных фракций.
В работе [9] приведены опытные данные по потерям напора при различных скоростях перекачки, в том числе и при критической скорости. В работе также приведен гранулометрический состав твердой фазы, что делается очень редко. Диаметр трубопровода D = 0,0762 м (3 inch). Несущая среда вода. Остальные исходные данные приведены в табл. 2.
Таблица 2
Значения плотности, грансостава твердых частиц, опытных и расчетных значений критических скоростей
|
Дисперсное вещество |
Кварц |
Сталь |
Оксид A? |
Кварц |
Сталь |
|
ρ p, кг/м3 |
2500 |
7950 |
3770 |
2500 |
7950 |
|
φ |
0,098 |
0,093 |
0,087 |
0,074 |
0,03 |
|
d5, мкм |
1,6 |
7,2 |
30,9 |
91,0 |
55,2 |
|
d10, мкм |
2,8 |
8,4 |
38,2 |
97,4 |
68,1 |
|
d20, мкм |
3,8 |
9,8 |
49,7 |
106,4 |
90,8 |
|
d30, мкм |
4,6 |
11,2 |
56,7 |
113,1 |
112,0 |
|
d40, мкм |
5,4 |
13,1 |
62,4 |
119,4 |
127,9 |
|
d50, мкм |
6,2 |
15,1 |
67,6 |
125,9 |
140,3 |
|
d60, мкм |
7,2 |
17,3 |
73,2 |
132,8 |
151,3 |
|
d70, мкм |
8,9 |
20,4 |
79,9 |
140,6 |
161,9 |
|
d80, мкм |
10,7 |
24,7 |
89,0 |
150,7 |
173,8 |
|
d90, мкм |
12,5 |
31,4 |
107,3 |
167,0 |
190,6 |
|
d95, мкм |
14,4 |
37,7 |
129,5 |
182,3 |
203,9 |
|
Ucr(exp), м/с |
0,366 |
0,762 |
0,914 |
1,219 |
2,438 |
|
Ucr(cal) (1), м/с, расчет по d50 |
0,43 |
1,44 |
1,385 |
1,53 |
2,37 |
|
Ucr(cal) (21) м/с, расчет по d50 |
1,22 |
2,01 |
1,39 |
1,45 |
2,17 |
|
Ucr(cal) (21) м/с, расчет по грансоставу |
– |
– |
1,48 |
1,47 |
2,16 |
|
Ucr(cal) (13), м/с, расчет по грансоставу и по d50 |
0,358 |
1,215 1,022 |
– |
– |
– |
При расчетах по формуле (1) принималось, что коэффициент сферичности S = 1, а эффективный диаметр частиц des равен фактическому среднему диаметру частиц d50. По форме, ближе всего к частицам сферической формы были кварцевые 100 мкм частицы, в меньшей мере 10 мкм кварцевые частицы. Стальные частицы в 100 мкм и 10 мкм имели произвольную форму, далекую от сферической, с оплавленными краями Частицы оксида алюминия имели также произвольную угловатую форму со сравнительно острыми ребрами. Плотность гидросмеси определяется по данным, приведенным в табл. 2. Из данных, представленных в табл. 2 следует, что расчеты по формуле (1) при использовании величин d50 с погрешностью порядка 20 % согласуются с опытными данными в случае частиц с крупными значениями d50 равными 125,7 мкм и 140,3 мкм. При дальнейшем уменьшении величины d50 расхождение возрастает до 50 % и 100 % и, неожиданно уменьшается до 20 % при d50 = 6,2 мкм, то есть при частицах броуновского масштаба. При расчете по формуле (2) с использованием величин d50 расхождение расчетных и опытных данных для крупных частиц примерно такого уровня, а при двух мелких фракциях, расхождение между опытными и расчетными значениями возрастает в большей мере. В предпоследней строке табл. 2 приведены результаты расчетов по формуле (2) с учетом возможности использования данных по гранулометрическому составу твердой фазы. В третьем, четвертом и пятом случаях результаты расчетов с учетом гранулометрического состава практически совпадают с аналогичными расчетами с использованием величин d50. Использовать выражение (2) для расчета критической скорости при гидротраспортировании частиц «пылевидных» фракций твердой фазы для 1 и 2 вариантов расчетов нет оснований, поскольку эта зависимость не содержит твердых частиц в области di ≤ 0,05 мм.
Расчет критической скорости при наличии частиц мельчайших фракций
В качестве одного из возможных способов учета наличия гранулометрического распределения твердых частиц в области di ≤ 0,05 мм положим что «пылевидные» частицы, определяемые по формуле (6) и меньшего размера, образуют совместно с жидкостью несущую среду, с плотностью и вязкостью, определяемых выражениями
ρ* / ρ = [1 – φ +( ρp / ρ) φ*] / (1 – φ + φ*);
µ* = µ (1 – φ*/0,65)-1,675, (7)
где φ* – объемная доля пылевидных частиц, размером меньших максимального размера dd *.
В формулу (2) входит отношение ν/ks, полученное для воды в трубе с технической шероховатостью стенки трубы, эквивалентной высоте песочной шероховатости 20 мкм. Поскольку предполагается, что частицы более крупных фракций перемещаются в несущей среде, образованных водой и «пылевидными» фракциями твердой фазы, то принимается, что справедливы следующие преобразования
ν/ks = µ /(ρ ks ) → µ*/(ρ* ks) = = µ (1 – φ*/0,65)-1,675/[(ρ*/ρ) ρks] =
= (ν/ks) ( – φ*/0,65)-1,675/(ρ*/ρ) = 0,05(1 – φ*/0,65)-1,675/(ρ*/ρ). (8)
Определим величину dd * не по скорости свободного осаждения частиц, а по скорости их стесненного осаждения [8], что в большей степени соответствует действительности,
Vs = V0 (1 – φ*)2,525/f* , (9)
где f* рассчитывается по формуле [8]
f* = [(1 – (6 φ*./π)2/3π/4]-0,5. (10)
С учетом последнего выражения получим, что
dd * = dd [f* / (1 – φ*)2,525]2/7. (11)
В условиях первого опыта при dd = 11,3 мкм при ожидаемом содержании пылевидных фракций φ* = 0, 098*0,9 = 0,0882 получим, что dd* = 12,5 мкм. То есть доля пылевидных частиц является преобладающей. В условиях второго опыта при dd = 5,4 мкм даже при максимально возможной объемной доли частиц φ* = 0,093 величин dd * = 5,9 мкм. Фактически же, в этом случае доле пылевидных частиц находится на уровне 2÷3 %, и их ожидаемое влияние на величину критической скорости будет незначительно.
Вторым моментом, который необходимо уточнить, являются значения коэффициентов транспортабельности di , которые, как следует из выражений (4), для частиц наименьшего класса определяется выражением ψi = 0,02; при di ≤ 0,05 мм. Это значение ψi = 0,02, при малой доли частиц фракций di ≤ 0,05 мм слабо влияет на результаты расчета критической скорости реальных промышленных гидросмесей, где доля пылевидных фракций крайне мала, так как при любых обогатительных процессах, они удаляются в процессе сгущения гидросмесей. В случае движения гидросмесей с преимущественным содержанием частиц пылевидных фракций необходимо более детальное дифференцированное задание коэффициентов транспортабельности для частиц такого класса.
В дальнейшем примем, что у частиц с di ≤ dd * коэффициент транспортабельности ψ равен нулю, то есть при di ≤ dd * ψ* = 0, а при больших значениях di он принимает следующие значения: при d1 = 0,05 мкм ψ1 = 0,01, а при d2 = 0,15 мкм ψ2 = 0,1. Аппроксимируя эти три пары значений di и ψi квадратичной зависимостью, получим
ψi = – a (di – dd *)2 + в (di – dd *), (12)
где
a = [ψ1 (d2 – dd *) – ψ2 (d1 – dd *)] / [(d2 – dd *)(d1 – dd *)(d2 – dd1)];
в = [ψ1 + a(d1 – dd *)2] / (d1 – dd *).
В результате выполненных преобразований, формула (2) преобразуется в выражение
Ucr = 3,3156[αgD (1 – φ*/0,65)-1,675/( ρ*/ρ)] 1/3(φψ)1/6, (13)
в котором выражение (φψ)1/6 рассчитывается по формулам (11) и (12), причем значения φ и φi относятся к частицам с d > dd * .
В последней строке табл. 2 приведены расчетные значения Ucr по формуле (13) для условий первого и второго опытов. Для первого опыта получено хорошее согласие расчетного значения Uc с опытным значением Ucr. Во втором опыте различие расчетного (верхнее значение) и опытного значения Uc сохраняется весьма значительным и составляет около 60 %, хотя и значительно меньше, в сравнении с прямым расчетом по зависимостям (1) и (2). Для условий второго опыта был проведен расчет критической скорости (нижнее значение) с использование значения d50, которое составило 1,022 м/с и расхождение с опытными данными уменьшилось примерно вдвое.
Для дальнейшего обоснования изложенной модели учета влияния пылевидных фракций на величину критической скорости двухфазного потока необходимо дальнейшее обобщение опытных данных и представление последних в возможно более широком объеме, в первую очередь в части гранулометрического состава частиц и фактической формы частиц. Важность последнего фактора, как было показано в работе [8], может стать определяющим. Поясним это следующим расчетным примером. Рассмотрим свободное осаждение трех частиц, имеющих различные формы: 1 – сопряженных по основанию двух прямых конусов с радиусом основания R и высотой каждого из конусов также R; 2 – те же конусы, между которыми расположена цилиндрическая вставка того же радиуса и высотой h = R: 3 – те же конусы, между которыми расположена цилиндрическая вставка того же радиуса и высотой h = 2R. Используя выражений (1), (3) и оставляя в правой части (4) только первый член, можно получить выражение для скорости свободного осаждения частиц при их различной ориентации в потоке [8]. Рассмотрим два варианта расположения частиц в потоке: 1 – вдоль оси конусов и 2 – в перпендикулярном направлении. Для отношения скорости в перпендикулярном направлении U+ к скорости в параллельном направлении к оси конусов U− имеет вид
U+ / U- = (de − / de + )(dm+ / dm−)2/. (14)
В табл. 3 приведены результаты расчетов по формуле (14).
Таблица 3
Отношение скоростей свободного осаждения при различной ориентации частиц в потоке
|
h / R |
0 |
1 |
2 |
|
U+ / U- |
0,67 |
1,24 |
1,82 |
Из этих расчетных оценок следует, что учет ориентации частицы относительно направления её движения является весьма существенным. Так, например, при осаждении конусообразной частицы, без цилиндрической вставки (h / R = 0), частица должна перемещаться с ориентацией оси конусов перпендикулярной к направлению осаждения, то есть она сориентируется в потоке на минимальное значение коэффициента лобового сопротивления. С возрастанием размера цилиндрической вставки (h /R > 0), частицы постепенно переориентируются осью конусов в направлении осаждения. Из этого примера следует, что, наряду с гранулометрическим составом, необходима полная информация о фактической форме частиц различной степени дисперсности. Примечательно также, что в выражение (14) не входит эффективный диаметр частицы dv, определенной по её массе, что ещё раз демонстрирует ограниченность применения его как единственной геометрической характеристики твердой фазы в дисперсных потоках. Подчеркнем, что в данном случае речь идет о пространственной ориентации частиц в пристенной зоне течения, где величина скорости в продольном направлении в кратность отличается от скорости в ядре потока при том же уровне скорости частиц в вертикальном направлении. Поэтому из общих физических представлений, можно ожидать, что если коэффициент сопротивления в вертикальном направлении возрастет, то величина критической скорости уменьшится. Для подтверждения такого предположения необходима опытная информация о геометрической форме частиц мельчайших фракций.
Заключение
Предложена уточненная формула расчета критической скорости гидротранспортирования при наличии мельчайших частиц твердой фазы. Максимальный размер частиц определен из условия равенства кинетической энергии осаждающейся частицы тепловой энергии молекулы жидкости. Показано, что имеющаяся экспериментальная информация о движении таких двухфазных потоков должна быть дополнена сведениями о фактической форме частиц мельчайших фракций.



