Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

В соответствии с принятой Правительством Российской Федерации в 2017 г. Программой «Цифровая экономика Российской Федерации» (на 2018–2024 гг.) ключевым фактором производства во всех сферах социально-экономической деятельности должны стать данные в цифровой форме. Определяющую роль в трансформации экономики в цифровую призваны сыграть два ключевых направления: а) исследования и разработки, б) кадры и образование. Основной целью направления «исследования и разработки» является создание системы поддержки поисковых, прикладных исследований в области цифровой экономики, обеспечивающей технологическую независимость и конкурентоспособность на глобальном уровне [1; 2].

Цель настоящего исследования: показать особенности и методы перевода на цифровую основу задач по выявлению, описанию и оценке тенденций в динамике взаимосвязей экономических показателей на примере сельского хозяйства региона. Для достижения поставленной цели решен ряд задач: сформированы таблицы с исходными данными показателей затрат в сельском хозяйстве Республики Дагестан за 2010–2016 гг.; разработан модельно-компьютерный инструментарий, реализующий системный подход, а также позволяющий автоматизировать все расчеты и процедуры обработки информации; построены уравнения рядов динамики, выражающие тенденции в динамике взаимосвязей между показателями; сформулированы выводы.

Данные в цифровой форме означают для экономических объектов, прежде всего, данные существующих учетно-отчетных документов, переведённые на компьютерную основу. Путем обработки учетно-отчетных данных создавать документы с аналитическими данными. Для этого применяется арсенал методов, созданный многими поколениями ученых и специалистов. Их принято классифицировать по различным признакам. Нами, например, они разделены на две группы: традиционные (основывающиеся на простых арифметических действиях и ручных расчетах) и новые (основывающиеся на высшей математике и компьютерных технологиях обработки данных). В настоящем исследовании применены в основном методы математического и компьютерного моделирования.

Показатели экономических объектов связаны друг с другом прямо или косвенно, образуя их системы. Выявить, описать и проанализировать эти связи является очень важной и в то же время сложной задачей экономической науки и практики. Главная сложность обусловлена стохастическим (или корреляционно-регрессионным) характером этих связей, означающим, что исследователю неизвестны ни степень, ни вид (характер) этих связей. Поэтому для выявления, описания и оценки связей возникает необходимость выполнения множества расчётов, часть из которых самa по себе не представляет ценности. Взаимосвязи и зависимости между различными показателями могут быть выявлены и оценены только с применением системного подхода, предусматривающий применения различных методик, методов, моделей и компьютерных инструментариев. Одни из экономических показателей являются зависимыми от одного, двух и более других, которые выступают как независимые показатели-факторы. Данные двух, трёх и более показателей для совокупности однотипных объектов называются пространственными данными, а математические модели, выражающие стохастические или корреляционные взаимосвязи между показателями для совокупности объектов, – уравнениями регрессии. Корреляционно взаимосвязанными могут быть два, три и более показателя одного и того же экономического объекта за ряд последовательных временных периодов. Такие данные называются рядами динамики, а математические модели, построенные на их основе, – уравнениями рядов динамики, выражающими тенденции во взаимосвязях [3; 4].

Настоящее исследование посвящено выявлению тенденций в динамике взаимосвязей между показателями затрат в сельском хозяйстве Республики Дагестан по данным за 2010–2016 гг. путем построения уравнений рядов динамики. При этом в качестве зависимых рассматриваются объемы всех затрат (в целом по сельскому хозяйству Республики Дагестан, в растениеводстве и животноводстве, тыс. руб.), а в качестве показателей-факторов – объемы материальных затрат и затрат на оплату труда (тыс. руб.).

Выявление и оценка взаимосвязей нами проведены для каждой пары показателей и для двухфакторных взаимосвязей. Примененный нами графический метод анализа показал, что, во-первых, зависимость всех затрат от материальных затрат во всех трех случаях одинаково четко выражена и имеет вид весьма близкий к линейному; во-вторых, корреляция в динамике зависимости всех затрат от затрат на оплату труда также имеет место, но ее вид заметно отличается.

Графический метод не позволяет однозначно утверждать о наличии и виде тенденций. Поэтому на приемлемость нами проверены различные виды уравнений. Для этого создана табл. 1.

По данным строк Yt и MZt можно построить уравнения, выражающие тенденции линейного и показательного видов; по данным первых трех строк – уравнение параболического вида; по данным строк Yt и 1/MZt – уравнение гиперболического вида и по данным строк lgYt и lgMZt – уравнение степенного вида.

По данным табл. 1 можно построить уравнения парной регрессии, выражающие тенденции с помощью «мастера функций» из MS Excel, используя две статистические функции «ЛИНЕЙН» и «ЛГРФПРИБЛ»: по второй функции – уравнение показательного вида, а по первой – остальные четыре.

Чтобы построить уравнения для зависимости всех затрат от затрат на оплату труда (Yt и ZPt), нет необходимости повторить выполнение всех процедур, описанных нами при построении уравнения для зависимости Yt от MZt. Для этого достаточно скопировать все таблицы, созданные для Yt от MZt, и заменить в копиях этих таблиц данные строк MZt данными ZPt. При этом данные всех расчетных строк автоматически пересчитываются.

Совокупность всех таблиц, созданных в MS Excel для построения уравнений регрессии, выражающих тенденции зависимостей Yt от MZt и от ZPt для сельского хозяйства в целом, можно рассматривать как компьютерную модель. Скопировав ее и заменив данные строк Yt, MZt, ZPt (в целом для сельского хозяйства) данными Yt, MZt, ZPt для растениеводства и животноводства, можно автоматически выполнить все расчеты, связанные с построением уравнений тенденций для растениеводства и животноводства. В табл. 2 приведены величины параметров и четырех статистических характеристик для уравнений рядов динамики линейного и степенного видов.

Из шести уравнений, данные по которым приведены в табл. 2, по всем статистическим характеристикам однозначно неприемлемой следует считать зависимость всех затрат в растениеводстве РД от затрат на оплату труда (r2 = 0; F = 0; А = 38,8 %); во всех случаях степень зависимости всех затрат (Yt) от материальных (MZt) выше, чем от затрат на оплату труда (ZPt); степень рассматриваемых зависимостей в животноводстве выше, чем в растениеводстве. Согласно четырём статистическим характеристикам (sey, r2, F, А) оба вида уравнений, выражающие зависимость всех затрат в сельском хозяйстве РД от материальных затрат в динамике за семь лет, следует считать приемлемыми для описания тенденций. Это вполне объяснимо; зависимости в экономике не могут однозначно считаться прямыми и/или кривыми линиями. Приемлемость разных видов уравнений для описания тенденций следует рассматривать как факт положительный; каждое уравнение позволяет получить информацию, дополняющую полученную по другим уравнением.

По статистическим характеристикам, рассчитанным нами, можно сформулировать два важных вывода о предпочтительности видов уравнений:

– по степени приемлемости (по величине r2) уравнения, выражающие зависимости, можно расположить в следующей последовательности:

а) для сельского хозяйства в целом: для Yt от MZt линейный – степенной – показательный; для Yt от ZPt линейный – показательный – степенной;

б) для растениеводства: для Yt от MZt линейный – показательный – степенной;

в) для животноводства: для Yt от MZt степенной – линейный – показательный; для Yt от ZPt линейный – степенной – показательный;

– по величинам средней ошибки аппроксимации (А, %) приемлемыми можно считать уравнения, выражающие зависимость Yt от MZt во всех трех сферах (сельское хозяйство в целом, растениеводство, животноводство), а выражающие зависимость Yt от ZPt – только в животноводстве.

Получить новую аналитическую информацию для оценки связей, зависимостей и тенденций можно и по каждому из уравнений. определив на их основе и проанализировав величины двух новых показателей: (а) предельного эффекта и (б) коэффициента эластичности, которые рассчитываются по формулам

а) dYt/dMZt; dYt/dZPt;

б) :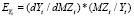

).

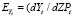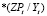Предельные эффекты и коэффициенты эластичности – новая ценная информация, характеризующая динамическую тенденцию. Предельный эффект – это величина (в тыс. руб.), на которую может возрасти Yt, если MZt (или ZPt) увеличится на 1 тыс. руб.; коэффициент эластичности показывает, на сколько процентов возрастет Yt, если величина MZt (или ZPt) увеличится на 1 %. В соответствии с предельным эффектом, определяемым по линейному уравнению, при увеличении материальных затрат в сельское хозяйство (MZt) на 1 тыс. руб. все затраты в сельское хозяйство РД в целом увеличатся на 1,3668 тыс. руб. А вот в соответствии с уравнениями степенного вида при увеличении MZt на 1 тыс. руб. неизвестно, на какую величину увеличивается Yt (она увеличивается на переменную величину, выраженную формулой).

При прочих равных условиях уравнениям линейного и степенного видов отдают предпочтение, поскольку параметр (m) при показателе-факторе имеет экономический смысл. Параметр (m) при показателе-факторе в уравнении линейного вида равен предельному эффекту показателя-фактора, а в уравнениях степенного вида – коэффициенту эластичности показателя-фактора. Предельный эффект показывает абсолютный рост зависимого показателя при увеличении показателя-фактора на одну абсолютную единицу, а коэффициент эластичности показывает величину роста зависимого показателя в процентах при увеличении фактора на 1 %.

Величины предельных эффектов и коэффициентов эластичности для построенных нами уравнений рядов динамики линейного и степенного видов приведены в табл. 3. Поскольку показатели Yt, MZt, ZPt выражают объемы затрат, то рост предельного эффекта не является фактом положительным; наоборот, меньший рост предельного эффекта в нашем случае означает снижение затрат. Следовательно, согласно табл. 3 как материальные (MZt), так и затраты на оплату труда (ZPt) в животноводстве более эффективны, чем в растениеводстве и сельском хозяйстве в целом. Коэффициент эластичности материальных затрат в животноводстве выше, чем в растениеводстве и в целом по сельскому хозяйству; но эластичность затрат на оплату – ниже. При исследовании связей, зависимостей и тенденций в экономике наряду с парными или однофакторными уравнениями регрессии принято строить и двух-трех и более факторные (многофакторные) уравнения, которые считаются более важными и ценными с точки зрения возможности получения новой информации.

Таблица 3

Величины предельных эффектов и коэффициентов эластичности, рассчитанные по уравнениям рядов динамики линейного и степенного видов, выражающих зависимость суммарных затрат в сельском хозяйстве РД от материальных затрат и от затрат на оплату труда по данным за 2010–2016 гг.

Поэтому наряду с однофакторными уравнениями Yt = f(MZt) и Yt = f(ZPt) нами построены двухфакторные уравнения Yt = f(MZt, ZPt). Уравнения линейного и степенного видов более приемлемы. Поэтому проанализируем параметры только этих уравнений.

Многофакторные уравнения в отличие от однофакторных позволяют рассчитывать и анализировать ряд дополнительных показателей. К ним относятся в первую очередь изокванты и предельные нормы взаимозаменяемости показателей-факторов [4; 5]. Изокванта – это уравнение, с помощью которого можно определить множество значений показателей-факторов, при которых результативный показатель принимает одно и то же значение. В нашем случае изокванты – это совокупности пар значений материальных затрат и затрат на оплату труда, при которой все затраты в каждой из трёх сфер (сельском хозяйстве в целом – Yt, в растениеводстве – YRt и животноводстве – YJt) принимают одни и те же значения (Yt = const; YRt = const; YJt = const). Чтобы построить изокванту, результативный показатель считается заданным и один из показателей-факторов выражается через другие.

Ниже приведены формулы изоквант для построенных нами двухфакторных уравнений: для уравнений линейного (а) и степенного (б) видов:

а) MZt = (Yt + 402482)/1,2902 – 1,3744*ZPt;

MZRt = (YRt – 54773)/1,3294 – 1,0724*ZPRt;

MZJt = (YJt – 385140)/1,0576 – 3,2356*ZPJt.

б) MZt = [Yt/(0,3656*ZPt0,3590)]1,2911;

MZRt = [YRt/(0,3022*ZPRt0,4112)]1,3360;

MZJt = [YJt/(0,3275*ZPJt0,4002)]1,3315.

Предельные нормы показателей-факторов представляют собой величины каждого из показателей-факторов, которые требуются, чтобы заменить одну единицу каждого из других. Они определяются как частные производные по уравнениям изоквант. Рассчитанные нами предельные нормы взаимозаменяемости материальных затрат и затрат на оплату труда в сельском хозяйств (а), растениеводстве (б) и животноводстве (в) РД приведены ниже:

а) ∂MZt/∂ZPt = 1,7733/1,2902 = 1,3744;

б) ∂MZRt/∂ZPRt = 1,4257/1,3294 = 1,0724;

в) ∂MZJt/∂ZPt = 3,4240/1,0576 = 3,2375.

В случае линейных уравнений рядов динамики предельные нормы взаимозаменяемости представляют собой численные величины, равные относительным параметрам (m1, m2) при показателях-факторах, которые определяются путем деления параметра при каждом показателе-факторе на каждый из остальных, и наоборот.

Заключение

Главным результатом проведённого исследования является модельно-компьютерный инструментарий (или компьютерная модель), предназначенный для построения пяти видов одно- и двухфакторных уравнений рядов динамики, апробированный по данным величин трех показателей затрат в сельском хозяйстве в целом, растениеводстве и животноводстве Республики Дагестан за 7 лет (2010–2016 гг.). Модельно-компьютерный инструментарий состоит из трех модулей: первый и второй – для построения одно- и двухфакторных уравнений рядов динамики соответственно, третий – для одновременного построения одно- и двухфакторных уравнений рядов динамики. Модельный инструментарий можно применить:

а) для любого региона;

б) для любого сельскохозяйственного предприятия;

в) по данным за любой интервал времени от пяти и более лет.