При мониторинге вентиляции лёгких человека методом электроимпедансной томографии (ЭИТ) [1] непрерывно формируются изображения поля изменения проводимости ΔΩ грудной полости. Основным источником изменения является изменение проводимости тканей легкого при наполнении их воздухом во время дыхания. На основании обработки полученных изображений можно оценить как интегральную вентиляцию легких ΔV(t), так и вентиляцию отдельных его частей. Данный «функциональный портрет» органа может быть использован при его идентификации на основании результатов реконструкции. Для определения интегрального изменения проводимости грудной полости достаточно проинтегрировать значения поля изменения проводимости грудной полости для каждого изображения. Полученный параметр – интегральное изменение проводимости грудной полости ΣΔΩ(t) – будет обладать высокой корреляцией с ΔV(t) [2]. Однако, реконструкция поля изменения проводимости грудной полости является некорректной задачей, что приводит к ошибкам и артефактам реконструкции [3]. Входные данные для реконструкции обладают малым изменением и измеряются с погрешностью, что так же затрудняет процесс реконструкции и добавляет ошибок и артефактов [3]. Таким образом, интегрирование результатов реконструкции приведет к накоплению ошибок реконструкции. Однако информация об изменении проводимости грудной полости хранится в измерительной информации ΔФ(t) для ЭИТ. Следовательно, можно оценить ΔV(t) по ΔФ(t) до реконструкции ΔΩ(t). Исследуем помехоустойчивость рассмотренных подходов.
Материалы и методы исследования
Для формирования измерительной информации для реконструкции поля изменения проводимости грудной полости ΔΩ(t) использовано численное моделирование. Использована модернизированная модель грудной полости, разработанная на базе модели из работы [4]. Геометрия задачи представлена на рис. 1.
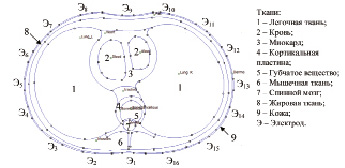
Рис. 1. Геометрия задачи для численного моделирования
Для моделирования мониторинга изменения проводимости грудной полости при вентиляции легких проводимость σ и диэлектрическая проницаемость ε тканей легкого изменялась по закону вентиляции легких ΔV(t). Для формирования массивов σ(t)и ε(t) на основании ΔV(t) используются значения σ и ε на вдохе и выдохе для заданной частоты инжектируемого тока fI. Формирование производится по формуле
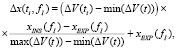 (1)
(1)
где x – искомый параметр (σ или ε), xINS – значение искомого параметра на вдохе; xEXP – значение искомого параметра на выдохе.
На рис. 2 представлены результаты формирования массива σ(t) при fI = 20 кГц для ΔV(t), полученной на основании результатов спирометрии.
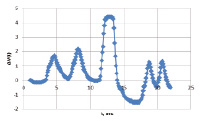
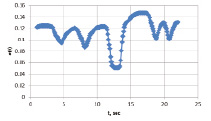
а) б)
Рис. 2. Графики зависимостей ΔV(t) (а) и σ(t) (б)
Для моделирования неоднородности разделения ΔV(t) между правым и левым легким введен коэффициент KVЛ, описывающий отношение изменения объема воздуха левого ΔVЛ(t) легкого к интегральному изменению объема лёгких ΔVЛ(t) и коэффициент KVП, описывающий отношение изменения объема воздуха правого ΔVП(t) легкого к интегральному изменению объема лёгких ΔV(t). Так, при KVЛ/KVП = 0,5/0,5 законы изменения Δσ(ti,fI) и Δε(ti,fI) для левого и правого легкого одинаковы. При KVЛ/KVП = 1/0 проводимость и диэлектрическая проницаемость левого легкого не изменяются и соответствуют значению глубочайшего выдоха. При KVЛ/KVП = 0,67/0,33 амплитуда закона изменения Δσ(ti,fI) и Δε(ti,fI) левого легкого в два раза больше, чем у правого.
Для каждой точки графика Δσ(ti,fI) и Δε(ti,fI) моделируется процесс получения измерительной информации ΔФ(ti) для ЭИТ, формируя тем самым массив ΔФ(t):
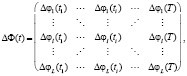 (2)
(2)
где L – число элементов вектора ΔФ(ti). На основании массива ΔФ(t) производится реконструкция поля изменения проводимости грудной полости ΔΩ(t). Для исследования влияния измерительных шумов к каждому значению Δφ добавлен шум с отношением сигнал/шум (SNR) равным [20; 30; 40; 50] дБ.
Результаты исследования и их обсуждение
На основании полученного массива ΔФ(t) с различным SNR произведена оценка интегральной вентиляционной функции (ИВФ) легких до и после реконструкции ΔΩ(t). Для оценки ИВФ до реконструкции применен интегральный параметр Ψ(t) [2], определяемый по формуле
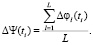 (3)
(3)
Для оценки ИВФ на основании ΔΩ(t) использовано ΣΔΩ(t), которое определяется по формуле
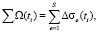 (4)
(4)
где Δσe(ti) – изменение проводимости e-го конечного элемента модели грудной полости в момент времени ti; S – число конечных элементов.
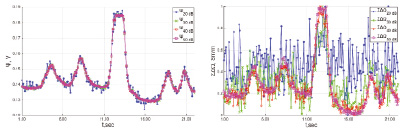
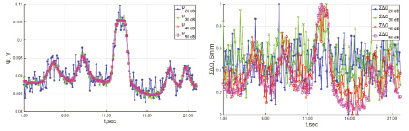
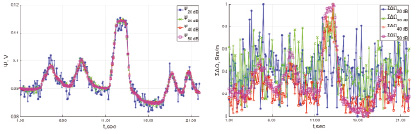
На рис. 3 представлены полученные графики ΣΔΩ(t) и Ψ(t) на основании результатов моделирования ΔФ(t) при SNR = [20; 30; 40; 50] дБ и KVЛ/KVП = [0,5/0,5; 1/0; 0,67/0,33].
|
KVЛ/KVП = 0,5/0,5 |
|
|
|
|
|
а) |
б) |
|
KVЛ/KVП = 1/0 |
|
|
|
|
|
в) |
г) |
|
KVЛ/KVП = 0,67/0,33 |
|
|
|
|
|
д) |
е) |
Рис. 3. Графики зависимостей Ψ(t) (а, в, д) и ΣΔΩ(t) (б, г, е) при SNR = [20; 30; 40; 50] дБ
Как видно из рис. 3, графики ΣΔΩ(t) и Ψ(t) имеют такой же закон изменения, как и ΔV(t). Однако с ростом уровня шумов входных данных зашумленность ΣΔΩ(t) увеличивается значительно быстрее чем зашумленность Ψ(t). Оценим уровень корреляции полученных графиков ΣΔΩ(t) и Ψ(t) с ΔV(t). Для этого рассчитаем коэффициент линейной корреляции Пирсона [5] по формуле
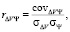 (5)
(5)
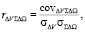 (6)
(6)
где σΔV – среднеквадратическое отклонение ΔV(t); σΨ – среднеквадратическое отклонение Ψ(t); σΣΔΩ(t) – среднеквадратическое отклонение ΣΔΩ(t); и интегрального параметра Ψ(t); covΔVΨ – ковариация ΔV(t) и интегрального параметра Ψ(t); covΔVΣΔΩ – к овариация ΔV(t) и интегрального параметра ΣΔΩ(t). Линейный коэффициент корреляции r может принимать значения в диапазоне [–1,1]. Знак обозначает направление связи (прямая или обратная).
Результаты расчета коэффициентов rΔVΨ и rΔVΣΔΩ при SNR = [20; 30; 40; 50] дБ и KVЛ/KVП = [0,5/0,5; 1/0; 0,67/0,33] представлены на рис. 4.
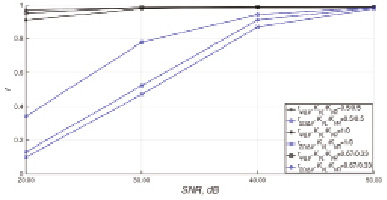
Рис. 4. Результаты расчетов rΔVΨ и rΔVΣΔΩ при SNR = [20; 30; 40; 50] дБ и KVЛ/KVП=[0,5/0,5; 1/0; 0,67/0,33]
Как видно из рис. 4, Ψ(t) сохраняет крайне высокую (r > 0,95) корреляцию с ΔV(t) вне зависимости от SNR и KVЛ/KVП. При этом корреляция между ΣΔΩ(t) и ΔV(t) значительно падает с уменьшением SNR и зависит от KVЛ/KVП. Следовательно, метод оценки ΔV(t) до реконструкции ΔΩ(t) на основании ΔФ(t) путем расчета Ψ(t) позволяет оценить ΔV(t) с высокой помехоустойчивостью.
Заключение
Предложен метод моделирования для исследования влияния вентиляции легких на результат мониторинга поля изменения проводимости грудной полости методом электроимпедансной томографии. На основании разработанной ранее модели грудной полости человека и предложенного метода мониторинга сформированы массивы измерительной информации для реконструкции поля проводимости внутренних структур биологических объектов. К данным добавлен шум заданного уровня и произведена оценка интегральной вентиляционной функции легких на основании результатов измерений и на основании результатов реконструкции. Исследование коэффициента корреляции между полученными значениями показало сохранение высокой степени корреляции с падением отношения сигнал-шум при различных соотношениях вентиляции левого и правого легкого. В то же время выявлено резкое падение корреляции между указанными величинами с падением отношения сигнал – шум, а также зависимость корреляции между соотношением изменения объема воздуха левого и правого легкого. Таким образом, метод оценки вентиляции легких до реконструкции на основании расчета измерительных данных позволяет оценить вентиляцию легких с высокой помехоустойчивостью. Данный метод может быть использован при идентификации легких с помощью ЭИТ путем выделения областей, наполняемых воздухом [6–8]. Для этого может быть использовано сравнение закона изменения проводимости конечного элемента и закона изменения вентиляции легких, что позволит повысить помехоустойчивость метода оценки регионарной вентиляции.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-38-00786 «Разработка методологии и алгоритмических средств интеллектуальной идентификации внутренних структур биологических объектов в системах электроимпедансной томографии».