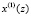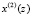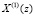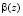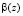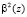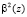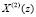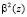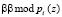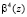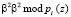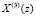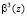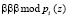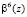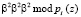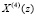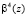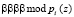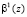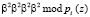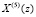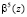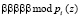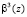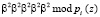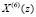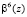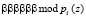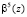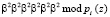Характерной чертой современных достижений в сфере инфотелекоммуникаций является широкое применение алгоритмов и методов цифровой обработки сигналов (ЦОС). Так, в работах [1, 2] показана реализация методов ЦОС в системах космической связи. Применение данных методов позволяет повысить помехоустойчивость в условиях мелких неоднородностей. В работах [3, 4] рассматривается использование методов ЦОС при выполнении цифровой фильтрации. В работах [5, 6] показана перспективность использования ортогональных преобразований сигналов в системах OFDM. Применение дискретного преобразования Фурье (ДПФ) и его быстрых алгоритмов в системах передачи информации, использующих стандарты IEEE 802.11, позволяет повысить скорость передачи данных при наиболее эффективном использовании радиочастотного ресурса. Однако быстрое преобразование Фурье (БПФ) характеризуется рядом недостатков, которые приводят к повышению схемных затрат и снижению точности выполнения ортогональных преобразований сигналов. Устранить такие недостатки возможно за счет использования теоретико-числовых преобразований (ТЧП), которые реализуются в полиномиальном модулярном коде (ПМК). Использование целочисленных вычислений в ПМК позволяет устранить ошибки округления и обеспечить преобразование сигнала при меньших схемных затратах. Повысить скорость выполнения ТЧП в ПМК возможно за счет применения систолических принципов вычислений. Поэтому разработка математической модели многоканальной систолической матрицы для выполнения теоретико-числовых преобразований сигналов в полиномиальном модулярном коде является актуальной задачей.
Известно, что использование целочисленных ортогональных преобразований сигналов, в частности теоретико-числовых преобразований, позволяет устранить ошибки округления, которые вызваны тригонометрическими поворачивающими коэффициентами ДПФ и БПФ. Кроме того, использование полиномиального модулярного кода приводит к повышению скорости выполнения ТЧП за счет распараллеливания вычислений на уровне арифметических модульных операций и использования табличной реализации [7]. Дальнейшее повышение скорости выполнения ТЧП возможно за счет применения параллельно-конвейерных вычислений, использующих систолические принципы построения. Поэтому целью статьи является повышение скорости вычисления ТЧП за счет разработки математической модели многоканальной систолической матрицы, функционирующей в ПМК.
Материалы и методы исследования
В настоящее время при выполнении ортогональных преобразований сигналов широко используются быстрые преобразования Фурье, которые задаются выражением
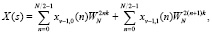 (1)
(1)
где 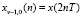 и
и 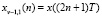 – отсчеты входного вектора, имеющие четные и нечетные номера соответственно;
– отсчеты входного вектора, имеющие четные и нечетные номера соответственно; 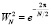 – поворачивающие коэффициенты БПФ.
– поворачивающие коэффициенты БПФ.
Анализ выражения (1) показывает, что использование косинусов и синусов в качестве поворачивающих коэффициентов WN приводит к значительным погрешностям округления. Устранить данный недостаток позволяет целочисленное ортогональное преобразование ТЧП. В этом случае снимаемый на выходе АЦП входной вектор x(n) представляет собой множество элементов поля GF(М). Тогда спектральные коэффициенты ТЧП определяются как
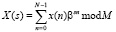 , (2)
, (2)
где 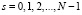 ;
; 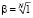 – порождающий элемент поля Галуа с характеристикой М.
– порождающий элемент поля Галуа с характеристикой М.
Ортогональные преобразования сигналов также можно выполнить в полях GF(pv)
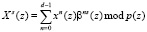 , (3)
, (3)
где 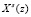 – s-я спектральная составляющая сигнала;
– s-я спектральная составляющая сигнала; 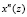 – n-й входной отсчет;
– n-й входной отсчет; 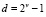 .
. 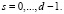
Повысить скорость выполнения ТЧП возможно за счет применения ПМК. В данном коде в качестве оснований используются неприводимые полиномы pi(z), где 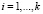 . В коде ПМК число Х сначала представляется в полиномиальной форме X(z), а затем в виде остатков
. В коде ПМК число Х сначала представляется в полиномиальной форме X(z), а затем в виде остатков 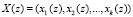 , где
, где 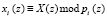 [7]. Тогда справедливо выражение
[7]. Тогда справедливо выражение
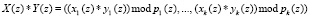 , (4)
, (4)
где 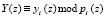 ; * – операция сложения, вычисления и умножения по модулю рi(z).
; * – операция сложения, вычисления и умножения по модулю рi(z).
Применяя полиномиальный модулярный код, получаем следующее ТЧП сигнала
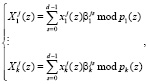 (5)
(5)
где 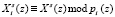 ;
; 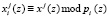 ;
; 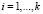 ;
; 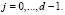
Однако выполнение ТЧП сигнала в ПМК требует временных затрат, соизмеримых с O(d2) операций модульных умножений. Дальнейшее снижение временных затрат на выполнение ТЧП возможно за счет применения систолических принципов вычислений [8]. При использовании систолических матриц преобразования (4) можно выполнить на основе рекуррентной схемы Горнера
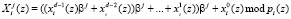 , (6)
, (6)
где 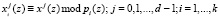 .
.
Тогда математическая модель систолического массива ТЧП в модулярном коде имеет вид
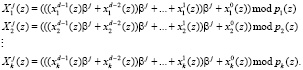 (7)
(7)
Проведя обобщение равенства (7), получаем математическую модель ТЧП сигналов в модулярном коде с использованием многоканальной систолической матрицы (МСМ)
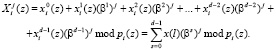 (8)
(8)
Так как МСМ состоит из однотипных процессорных элементов (ПЭ), то каждый из ПЭ (s = 1, 2, …, d), выполняет следующую базовую операцию
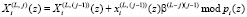 , (9)
, (9)
где 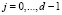 ; L – текущий такт вычислений в j-й ячейке;
; L – текущий такт вычислений в j-й ячейке; 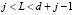 ,
, 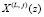 – записанное в регистр РгS на L-м такте значение суммы;
– записанное в регистр РгS на L-м такте значение суммы; 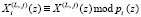 ;
; 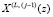 – записанное в регистр РгS на (L – 1)-м такте вычисленное значение суммы;
– записанное в регистр РгS на (L – 1)-м такте вычисленное значение суммы; 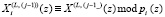 ;
; 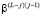 – поворачивающий коэффициент на входе j-й ячейки МСМ в L-й такт работы.
– поворачивающий коэффициент на входе j-й ячейки МСМ в L-й такт работы.
Результаты исследования и их обсуждение
Пусть задан ПМК, имеющий основания 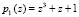 и
и 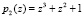 . Данные полиномы имеют мультипликативные группы порядка d = 7. Значит, такой ПМК способен выполнить 7-точечную реализацию ТЧП сигнала. Тогда получаем
. Данные полиномы имеют мультипликативные группы порядка d = 7. Значит, такой ПМК способен выполнить 7-точечную реализацию ТЧП сигнала. Тогда получаем
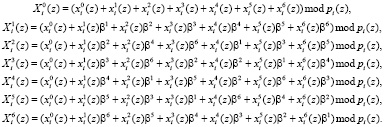
Для разработки структуры МСМ, реализующей ТЧП в ПМК, составим таблицу, в которой показан процесс получения спектральных отсчетов для 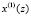 и
и 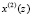 .
.
Получение спектральных составляющих ТЧП в МПК
|
Спектр Х(j) |
Входной отсчет |
Входной отсчет |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщая результаты, представленные в таблице, получаем следующее выражение
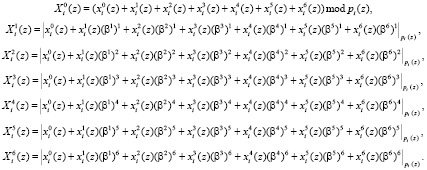
Схемная реализация разработанной математической модели МСМ, реализующей ТЧП сигналов в ПМК с основаниями 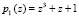 и
и 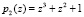 , показана на рис. 1. Каждый из ПЭ состоит из двух регистров (Рг), которые предназначены для записи отсчетов входного вектора
, показана на рис. 1. Каждый из ПЭ состоит из двух регистров (Рг), которые предназначены для записи отсчетов входного вектора 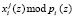 и поворачивающего вектора
и поворачивающего вектора 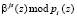 . Для реализации выражения (7) используются умножитель (Ум) по модулю pi(z), где i = 1, 2, и сумматор (Cум) по модулю два. Для хранения промежуточного результата используется регистр (РгS). На рис. 2 приведена временная диаграмма вычисления ТЧП сигнала в МСМ.
. Для реализации выражения (7) используются умножитель (Ум) по модулю pi(z), где i = 1, 2, и сумматор (Cум) по модулю два. Для хранения промежуточного результата используется регистр (РгS). На рис. 2 приведена временная диаграмма вычисления ТЧП сигнала в МСМ.
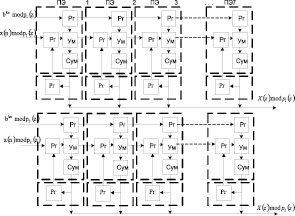
Рис. 1. Схемная реализация математической модели МСМ ТЧП, функционирующей в ПМК
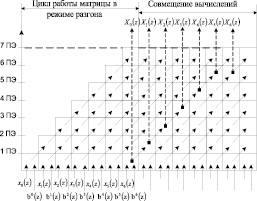
Рис. 2. Временная диаграмма вычисления ТЧП в МСМ
Анализ разработанной математической модели ТЧП сигнала в МСМ показал, что начальная загрузка матрицы составляет d = 7 тактов. При этом количество тактов, составляющих один цикл вычислений, равно 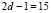 . Из рис. 2 наглядно видно, что коэффициент эффективности применения оборудования в разработанной математической модели МСМ вычислений ТЧП составляет Q = 1. Очевидно, что время реализации базовой операции ПЭ определяется
. Из рис. 2 наглядно видно, что коэффициент эффективности применения оборудования в разработанной математической модели МСМ вычислений ТЧП составляет Q = 1. Очевидно, что время реализации базовой операции ПЭ определяется
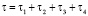 , (10)
, (10)
где t1 – время реализации процедуры приема-передачи данных в ПЭ; t2 – время модульного умножения; t3 – время выполнения операции суммирования по модулю два; t4 – время необходимое на выполнение процедуры записи и считывания результата вычислений.
Время реализации ТЧП сигнала в ПМК на основе разработанной модели МСМ составит
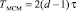 . (11)
. (11)
Рассмотрим работу разработанной МСМ по основанию р1(z). Перед началом работы регистры РгS МСМ обнуляются. На первом такте работы значения 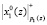 ,
, 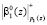 поступают в ПЭ1. Спустя время t1 + t2 выполняется суммирование по модулю два
поступают в ПЭ1. Спустя время t1 + t2 выполняется суммирование по модулю два 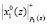 с содержимым РгS. Промежуточный результат суммирования на микротакте t4 заносится в регистр РгS. Во время второго такта работы значения
с содержимым РгS. Промежуточный результат суммирования на микротакте t4 заносится в регистр РгS. Во время второго такта работы значения 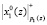 и
и 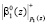 с выхода ПЭ1 подаются в ПЭ2. Одновременно в ПЭ1 поступают
с выхода ПЭ1 подаются в ПЭ2. Одновременно в ПЭ1 поступают 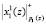 и
и 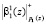 . На микротакте t2 второго такта
. На микротакте t2 второго такта 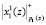 задерживается в элементе задержки и одновременно в ПЭ2 вычисляется
задерживается в элементе задержки и одновременно в ПЭ2 вычисляется 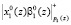 . Затем в ПЭ1 и ПЭ2 на микротакте tз происходит суммирование по модулю два, а на микротакте t4 полученные суммы записываются в регистры РгS1 и РгS2. В дальнейшем все ПЭ работают синхронно. На третьем такте выполняются переводы:
. Затем в ПЭ1 и ПЭ2 на микротакте tз происходит суммирование по модулю два, а на микротакте t4 полученные суммы записываются в регистры РгS1 и РгS2. В дальнейшем все ПЭ работают синхронно. На третьем такте выполняются переводы: 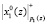 и
и 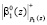 – в ПЭ3;
– в ПЭ3; 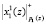 и
и 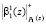 – в ПЭ2;
– в ПЭ2; 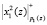 и
и 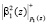 – в ПЭ1. Теперь три ПЭ (L = 1, 2, 3) работают синхронно. На четвертом такте работу начинает ПЭ4, куда поступают
– в ПЭ1. Теперь три ПЭ (L = 1, 2, 3) работают синхронно. На четвертом такте работу начинает ПЭ4, куда поступают 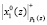 и
и 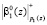 . На пятом такте в работу включается ПЭ5, на шестом такте – ПЭ6, на седьмом такте – ПЭ7. При этом все ПЭ работают синхронно.
. На пятом такте в работу включается ПЭ5, на шестом такте – ПЭ6, на седьмом такте – ПЭ7. При этом все ПЭ работают синхронно.
Как видно из рис. 2, на d = 7 такте МСМ закончила процедуру загрузки и разгонки. В конце данного такта результат 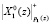 , полученный в ПЭ1, поступает на выход МСМ. На следующем такте значение спектральной составляющей
, полученный в ПЭ1, поступает на выход МСМ. На следующем такте значение спектральной составляющей 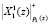 будет получено в ПЭ2. На (d + 2) = 9 такте результат
будет получено в ПЭ2. На (d + 2) = 9 такте результат 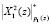 будет получен в ПЭ3 и т.д. Значит, время выдачи результатов будет составлять период равный
будет получен в ПЭ3 и т.д. Значит, время выдачи результатов будет составлять период равный 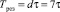 . Чтобы не тормозить работу конвейера на (d + 1) = 8 такте, на вход ПЭ1 МСМ поступают данные
. Чтобы не тормозить работу конвейера на (d + 1) = 8 такте, на вход ПЭ1 МСМ поступают данные 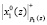 и
и 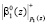 .
.
Переход к МПК позволяет повысить скорость базовой операции ТЧП (9). В этом случае 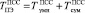 , где
, где 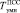 и
и 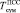 – временные затраты на реализацию операции умножения и сложения. Пусть разрядность модуля d = deg Р(z) = 30. Если в МСМ использовать умножитель матричного типа, то
– временные затраты на реализацию операции умножения и сложения. Пусть разрядность модуля d = deg Р(z) = 30. Если в МСМ использовать умножитель матричного типа, то 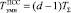 , где ТS – время суммирования в одноразрядном сумматоре. Пусть значение ТS = 15 нс. При обработке 30-разрядных данных на базовую операцию ТЧП потребуется
, где ТS – время суммирования в одноразрядном сумматоре. Пусть значение ТS = 15 нс. При обработке 30-разрядных данных на базовую операцию ТЧП потребуется 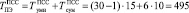 нс.
нс.
Вычислим временные затраты на базовую операцию ТЧП в МПК. Для d = deg Р(z) = 30 возможно использовать шесть модулей разрядности 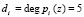 , где i = 1, 2,.., 6. Для выполнения операций сложения и умножения по модулю pi(z) можно использовать LUT-таблицы (ПЗУ 1636РР1У), время выборки которых составляет Твыб = 65 нс. Тогда время выполнения базовой операции ТЧП равно
, где i = 1, 2,.., 6. Для выполнения операций сложения и умножения по модулю pi(z) можно использовать LUT-таблицы (ПЗУ 1636РР1У), время выборки которых составляет Твыб = 65 нс. Тогда время выполнения базовой операции ТЧП равно 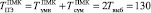 нс. Значит, применение ПМК повышает скорость выполнения базовой операции ТЧП в 3,8 раза. Кроме того, использование разработанной математической модели МСМ позволило повысить скорость выполнения ТЧП на 10 % по сравнению с чисто-систолической моделью вычислений ТЧП и 14,9 раза по сравнению c классическим выполнением ТЧП в GF(25).
нс. Значит, применение ПМК повышает скорость выполнения базовой операции ТЧП в 3,8 раза. Кроме того, использование разработанной математической модели МСМ позволило повысить скорость выполнения ТЧП на 10 % по сравнению с чисто-систолической моделью вычислений ТЧП и 14,9 раза по сравнению c классическим выполнением ТЧП в GF(25).
Заключение
Применение ТЧП в задачах ЦОС минимизирует ошибки округления, которые получаются при использовании БПФ. Использование разработанной математической модели МСМ, функционирующей в ПМК позволяет повысить скорость вычисления базовой операции ТЧП в 3,8 раза при обработке 30-разрядных данных. А применение алгоритма МСМ позволило повысить скорость выполнения ТЧП на 10 % по сравнению с чисто-систолической моделью вычислений ТЧП и 14,9 раза по сравнению c классическим выполнением ТЧП в GF(25).
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-37-00009.