Решая задачу проектирования технических систем сетевого типа (электрические и транспортные сети, системы городского тепло- и водоснабжения и аналогичные им), необходимо применение подходящей математической модели, которая удовлетворяла бы требованиям соблюдения критериев экономичности и надежности. Если вести речь о начальном этапе проектирования сети, то структура будет иметь обобщенный вид без существенной детализации. В этом отношении критерии, нашедшие свое отражение в модели, будут учтены в обобщенном виде. Тем не менее такая модель послужит отправной точкой в построении оптимальной структуры системы, то есть основой для последующего детального проектирования.
Рассматривая задачу построения оптимальной структуры на ранних этапах проектирования, сделаем акцент не на минимизации затрат, а на соблюдении граничных условий структурной надежности. В основе построения условий лежит теория надежности, которая для решения данной задачи предлагает искать решение с использованием теории вероятностей и статистических данных, подчиняющихся известным законам случайного распределения. Предварительная проработанность вопросов выбора оптимальной структуры по критерию надежности рассматривалась в работах [1, 2], а в [3] анализировались возможные методы оценки показателей надежности. Фактически в данных работах рассматривались возможности построения оптимальной структуры с помощью математических моделей, реализация которых позволяла бы выразить критерий надежности не в качественной, а в количественной форме. Поскольку структурная надежность системы тесно связана с вероятностной природой появления нежелательных событий, то процесс формализации задачи оптимизации более сложных структур становится затруднительным. В подтверждение сказанного, в работе [4] показана сложность процедуры определения вероятности связи «источник – потребитель» в структуре. Следовательно, при построении математической модели, в которой величины вероятностей были бы преобразованы в формат меры неопределенности информации, это облегчило бы поиск оптимального решения.
Далее предложим экономико-математическую модель описания задачи поиска оптимальной структуры исходя из поиска минимума затрат при соблюдении граничных условий структурной надежности, характеризующихся применением меры неопределенности информации.
Роль неопределенности информации в задаче построения структуры системы
Любая система подвержена разнообразным воздействиям случайного характера, поэтому трудно предположить, в каком она состоянии будет находиться в тот или иной момент времени, что свидетельствует о наличии неопределенности. Под воздействием нежелательных факторов меняются структура и состояние системы, что и отражается на уровне её надежности. Накопление, обработка и систематизация информации о состояниях системы пополняет знания и позволяет вырабатывать более эффективные решения при её проектировании и эксплуатации.
Из теории информации [5, 6] известно, что неопределенность характеризуется количеством информационной энтропии, применимость которой, в частности, представлена в работах [7, 8]. Она также может быть выражена в количественной и качественной форме. Качественная составляющая энтропии отражает работоспособное и неработоспособное состояния системы, а количественную составляющая можно определить опираясь на классическую модель К. Шеннона об информации и энтропии [9]: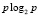 
где p – вероятность проявления события или вероятность нахождения объекта в том или ином состоянии. Ключевую роль данная формула играет в задачах выбора из множества альтернатив. В работах [10, 11] предложены методы определения количества информации в сложных инженерных системах и в условиях эпистемической неопределенности, а в [4, 12–14] отражены возможности её применения в задачах оценки состояния структуры системы. В данных работах не исключается важность и возможности применения модели Клода Шеннона, которая необходима для построения оптимальной структуры сети. Модель не исключает возможностей построения математической модели и расчета количества информационной энтропии, присущей связи «источник – потребитель» рассматриваемой структуры. Тем самым, мера неопределенности информации играет существенную роль в измерении уровня структурной надежности через количество информационной энтропии.
Экономико-математическая модель построения структуры
Предварительным этапом решения задачи является подготовка исходных данных: определение совокупности показателей, характеризующих состояния элементов системы. Структуру можно представить в виде графа, в котором: ul∈U1 (l = 1, 2, ..., m) – множество вершин (вершины имитируют наличие единственного источника u0 и множество потребителей в количестве m); xi∈X – множество дуг (имитирующие связанные между собой элементы структуры). Каждой дуге i (элемент сети) приписаны: ci – стоимость i-го элемента; pi – вероятность появления события (меняющего состояние элемента). Структура системы рассматривается в виде направленного графа, отображающего связи источника энергии со многими потребителями. Поскольку оптимальная структура на предварительном этапе обработки исходных данных не может быть построена, то речь будет идти о рассмотрении избыточной структуры, изображаемой графом, близким по свойствам с полносвязным графом.
В обобщенном виде экономико-математическая модель имеет следующий вид:
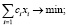(1)
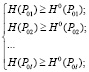(2)
xi = [0; 1], (3)
где ci – стоимость элемента i, выраженная в валюте; l – номер потребителя энергии; 0 – номер источника питания; H(P0l) – энтропия работоспособного состояния связи 0-l, по которой протекает энергия от источника к потребителю; H0(P0l) – заданная граничная величина энтропии как меры обеспечения бесперебойного снабжения энергией по связи 0-l потребителя l; P0l – вероятность работоспособного состояния связи 0-l.
Для построения левых частей системы (2) воспользуемся моделью Шеннона и методами построения путей, представленными в работах [4, 13]. В качестве примера возьмем «мостиковую схему». В этой схеме, имеющей вид неориентированного графа, имеется один источник и три потребителя (на рис. 1 – вершины 1, 2 и 3), которые снабжаются энергией от единственного источника (вершина 0).
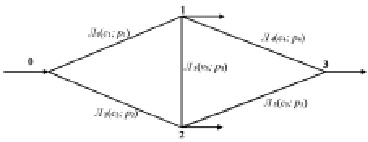
Мостиковая схема
Каждой ветви графа приписываются вероятности работоспособного состояния элементов (p) и прогнозируемые затраты на строительство каждого элемента (c).
Для определения энтропии работоспособного состояния H(P0l) связей «источник – потребитель» предложим способ, включающий в себя учет всех совместных состояний элементов, присущих каждому из путей в структуре от источника к рассматриваемому потребителю.
Определение энтропии на основе теорем сложения и умножения вероятностей
Воспользуемся теоремами сложения и умножения вероятностей пересекающихся событий A для определения полной вероятности работоспособного состояния связи 0-l (при известной вероятности минимального пути,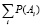 
):
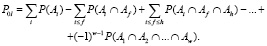(4)
Используя (4), выражения для расчета вероятности связей (с учетом перебора всех возможных состояний элементов) будут иметь вид
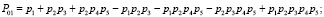
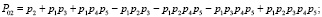
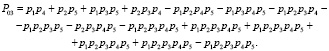
Если в качестве примера рассмотреть порядок пересечения и сложения событий для определения P03, то он будет иметь вид
A1 + A2 + A3 + A4 – A1∩A2 – A1∩A3 – A1∩A4 – A2∩A3 – A2∩A4 – A3∩A4 + A1∩A2∩A3 +
+ A1∩A2∩A4 + A1∩A3∩A4 + A2∩A3∩A4 – A1∩A2∩A3∩A4,
где A1 = p1p4, A2 = p2p5, A3 = p1p3p5, A4 = p2p3p4.
Первые слагаемые в данных выражениях позволяют рассчитывать вероятности минимальных путей на графе.
Полученные выражения расчета P0l применимы для определения энтропии H0l работоспособного состояния связи 0-l. Воспользуемся формулой Шеннона, согласно которой величина энтропии работоспособного состояния элемента i структуры определяется по выражению
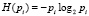. (5)
Тогда по аналогии с (4) и на основе (5), энтропия работоспособного состояния связей в структуре (рисунок) определится по выражениям
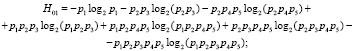
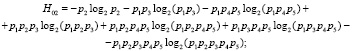
Эти математические выражения формируют левые части ограничений в задаче (1)–(3). При определении величин H0l не исключен учет отдельных свойств, присущих энтропии Шеннона: 1) при p = 1,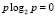 
; 2) при p = 0, 
.
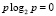С точки зрения необходимости соблюдения уровня структурной надежности сети, граничные величины H0(P0l) определяются из условия о допущении проектировщиком или эксплуатационником возможного перерыва в энергообеспечении группы или отдельных потребителей по выражению (учитывая обоснования в [14]):
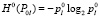, (6)
где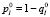 
– вероятность допустимого бесперебойного энергоснабжения потребителя l по связи 0-l; 
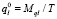– вероятность допустимого перерыва в энергоснабжении потребителя l; Mqj – среднее время (в часах), в течение которого допускается перерыв в энергоснабжении потребителя; T – число часов в году.
Представим пример решения (6). Пусть в узле l сети требуется обеспечить надежность при соблюдении условия: среднее время, в течение которого допустимый перерыв в энергоснабжении потребителя, не должен быть более Mqj = 80 часов в год. Число часов в году – T = 8760. Вероятность допустимого перерыва в энергоснабжении потребителя l –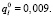 
Тогда по (6), 
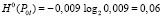бит.
Решение задачи оптимизации (1)–(3) возможно, например, методом ветвей и границ, представленным в [15]. Однако отметим следующее: большинство ограничений в (2), их левые части, имеют большое количество слагаемых, являясь громоздкими, так как учитывают все варианты состояний элементов связи. Тем самым (особенно для сложных структур) затягивается по времени поиск решения.
Система ограничений (2) в задаче оптимизации может быть представлена в виде неравенства:
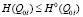, (7)
где H(Q0l) – энтропия неработоспособного состояния связи 0-l,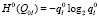 
– граничная величина энтропии как меры перерыва в снабжении энергией потребителя l по связи 0-l, Q0l – вероятность неработоспособного состояния связи 0-l, 
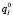– вероятность допустимого перерыва энергоснабжения потребителя l.
Неравенства строятся аналогично способу учета всех возможных состояний, представленному выше.
Заключение
Рассматриваемая задача касается вопросов построения оптимальной сетевой структуры технической системы в общем виде, то есть без учета факторов, детализирующих её функциональные возможности. Построение структуры связано с соблюдением критериев экономичности и надежности. Отличительной особенностью предлагаемой математической модели построения оптимальной структуры является учет критерия надежности через применение меры неопределенности информации. В качестве неё взята информационная энтропия. Для её определения используются математические выражения, а в качестве исходных данных взяты показатели структурной надежности сети. Каждое из неравенств системы нелинейных ограничений задачи отражает сопоставление расчетной величины энтропии связи «источник – потребитель» с граничной величиной энтропии, определяемой на основе требования к соблюдению необходимого уровня надежности данной связи. Сопоставление в ходе вычислений расчетной и граничной величин энтропии позволяет сделать вывод о возможности сети обеспечить заданный уровень надежности в обеспечении энергией потребителей. Предлагаемая математическая модель является нелинейной, направлена на поиск целочисленного решения и тем самым позволяет строить структуры как разомкнутого, так и замкнутого типа.
Работа выполнена при поддержке Фонда содействия инновациям по программе «УМНИК» в рамках договора № 13138ГУ/2018 от 23.05.2018.