Анализ характеристик электромагнитных полей, распространяющихся в стохастических неоднородных средах, можно проводить на основе прямого компьютерного моделирования с использованием методов классической теории вероятностей, имеющей дело с последовательностями независимых случайных величин. Наиболее распространенными в вероятностных расчетах являются числительные алгоритмы, основанные на методе Монте-Карло [1]. Значительные результаты в вероятностных исследованиях полей были получены благодаря использованию лучевых представлений [2]. Это стало возможным благодаря относительно простой математической конструкции и наглядности лучевого приближения. В основе геометрооптического решения волнового уравнения для поля лежит предположение о медленности изменения параметров среды и характеристик поля в масштабе длины волны в среде. В схеме Монте-Карло для каждой реализации пространственного распределения неоднородностей стохастической среды рассчитываются траекторные характеристики поля. Набирая ансамбль реализаций траекторных характеристик и проводя усреднение по всем реализациям среды, можно получить статистические моменты траекторных характеристик. Однако при таком подходе имеется большая проблема, связанная с тем, что при решении краевой задачи для каждой реализации среды необходимо проводить пристрелку случайных траекторий в пункт наблюдений. Этот способ требует значительных затрат времени компьютера и для высокой точности пристрелки трудно реализуем. Если необходимо определить зависимости статистических траекторных характеристик поля от дистанции, то задача существенно усложняется и указанную процедуру необходимо выполнить для набора координат приемного пункта. Кроме того, метод статистических испытаний не позволяет установить функциональные связи между флуктуирующими характеристиками электромагнитного поля и параметрами среды.
Кроме метода Монте-Карло для решения траекторной задачи в стохастических неоднородных средах успешно используют асимптотические разложения [3]. Использование корреляционной функции неоднородностей среды, в целом описывающей случайное поле неоднородностей, позволяет отказаться от метода статистических испытаний и непосредственно рассчитать статистические характеристики электромагнитного поля. Наряду с известными достоинствами асимптотических методов, такими как относительная простота при получении решения стохастических задач, а также отсутствие трудностей численных методов, связанных с большим количеством вычислений и плохой предсказуемостью результатов, они обладают и недостатками. Прежде всего, это медленная сходимость решений в отдельных случаях и ограниченная область применимости. Кроме того, результатом использования асимптотических методов, как правило, являются сложные интегральные выражения, которые удается привести к аналитическому виду только в некоторых частных случаях.
Цель работы заключается в создании оперативной схемы численно-аналитической алгоритмизации лучевого приближения для электромагнитного поля в стохастических неоднородных средах с использованием численного интегрирования и асимптотических разложений.
Результаты исследования и их обсуждение
Рассмотрим одну из возможных схем оперативной алгоритмизации расчетов характеристик лучевого поля с использованием численных и аналитических методов на примере вычислений флуктуаций фазы и направления распространения лучей в стохастической неоднородной среде.
Согласно лучевому приближению для фазы поля, распространяющегося в стохастической среде, имеем [3]:
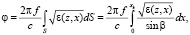 (1)
(1)
где ε – случайная функция диэлектрической проницаемости среды, c – скорость света в вакууме, f – рабочая частота, β – угол рефракции луча, dS – элемент дуги, xk – дистанция.
Определим флуктуацию фазы поля в первом приближении метода возмущений. Полагая
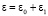 , (2)
, (2)
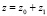 , (3)
, (3)
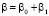 (4)
(4)
и считая 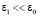 , решение (1) будем искать в виде:
, решение (1) будем искать в виде: 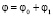 . Подставляя разложения (2)–(4) в формулу (1), в первом приближении для флуктуаций фазы получаем
. Подставляя разложения (2)–(4) в формулу (1), в первом приближении для флуктуаций фазы получаем
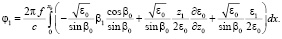 (5)
(5)
В подынтегральную функцию формулы (5) входят флуктуации траекторных характеристик β1, z1 которые можно определить, решая методом возмущений систему лучевых уравнений. Запишем лучевые уравнения в виде [2]:
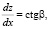 (6)
(6)
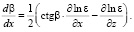 (7)
(7)
Подставляя (2)–(4) в уравнения (6), (7) и проводя линеаризацию, получаем систему уравнений для флуктуаций траектории:
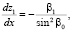 (8)
(8)
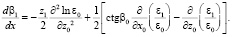 (9)
(9)
Выражая β1 из уравнения (8) и подставляя его в (5), имеем
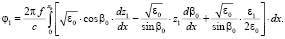 (10)
(10)
Интегрируя (10) и учитывая граничные условия задачи, получаем
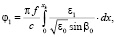 (11)
(11)
где интегрирование проводится по невозмущенной траектории, а в подынтегральной функции отсутствуют флуктуации траекторных характеристик. Заметим, что для расчета флуктуаций фазы при малых углах падения волны на среду использование системы (6),(7) не корректно, поскольку в правых частях уравнений возникает особенность. В связи с этим в дальнейших аналитических преобразованиях целесообразно перейти к новой независимой переменной в виде элемента группового запаздывания волны 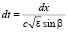 . Переходя в (11) к переменной dt, получаем
. Переходя в (11) к переменной dt, получаем
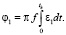 (12)
(12)
Для расчета флуктуаций направления распространения поля сделаем замену независимой переменной в системе (6), (7). В результате преобразований имеем
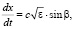 (13)
(13)
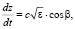 (14)
(14)
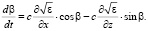 (15)
(15)
Следует заметить, что все проводимые здесь аналитические преобразования относятся к электромагнитным полям. Вместе с тем эти преобразования применимы и к случаю распространения звуковых полей в стохастических диэлектрических средах, например, звукового поля в атмосфере и океане. В этом случае в системе уравнений (13)–(15) вместо функции 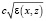 следует рассматривать локальную скорость звука V(x, z), а в качестве градиентов
следует рассматривать локальную скорость звука V(x, z), а в качестве градиентов 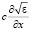 и
и 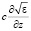 использовать градиенты
использовать градиенты 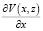 и
и 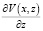 . Подставляя разложения (2)–(4) в систему (13)–(15) и проводя линеаризацию, для флуктуаций траекторных характеристик получаем
. Подставляя разложения (2)–(4) в систему (13)–(15) и проводя линеаризацию, для флуктуаций траекторных характеристик получаем
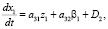 (16)
(16)
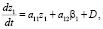 (17)
(17)
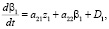 (18)
(18)
где 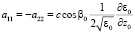 ,
, 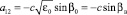 ,
, 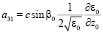 ,
,
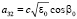 ,
, 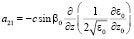 ,
, 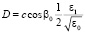 , (19)
, (19)
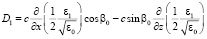 ,
, 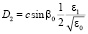
(здесь βн начальный угол падения луча на среду и учтен закон преломления: 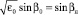 [2]). Нетрудно заметить, что уравнения (17), (18) образуют систему, которую можно решать независимо от уравнения (16). Используя теорему о существовании производных по свободным параметрам от решения порождающей системы дифференциальных уравнений (14), (15) (при ε1 = 0) [4], можно решить систему (17), (18). Как известно [4], такие производные в совокупности образуют фундаментальные решения линейной однородной системы уравнений для флуктуаций (17), (18).
[2]). Нетрудно заметить, что уравнения (17), (18) образуют систему, которую можно решать независимо от уравнения (16). Используя теорему о существовании производных по свободным параметрам от решения порождающей системы дифференциальных уравнений (14), (15) (при ε1 = 0) [4], можно решить систему (17), (18). Как известно [4], такие производные в совокупности образуют фундаментальные решения линейной однородной системы уравнений для флуктуаций (17), (18).
Решая (17), (18), имеем
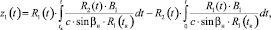 (20)
(20)
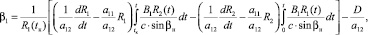 (21)
(21)
где 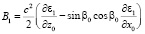 , R1(t), R2(t) – фундаментальные решения.
, R1(t), R2(t) – фундаментальные решения.
Для решения краевой задачи в качестве фундаментальных решений возьмем
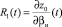 ,
, 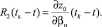 (22)
(22)
При этом 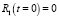 ,
, 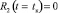 . Формула (21) позволяет рассчитать флуктуации направления распространения лучевого поля вдоль всей невозмущенной траектории. В частности, в пункте приема (когда t = tк) имеем
. Формула (21) позволяет рассчитать флуктуации направления распространения лучевого поля вдоль всей невозмущенной траектории. В частности, в пункте приема (когда t = tк) имеем
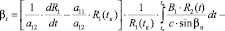
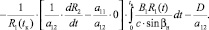
Учитывая равенство нулю первого интеграла, получаем:
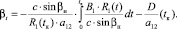
Подставляя значения коэффициентов (19) при t = tк, окончательно имеем
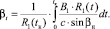 (23)
(23)
В случае, когда 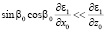 (пологие наклонные траектории лучей или присутствие в среде слоистых неоднородностей, вытянутых вдоль оси x), для флуктуации направления распространения лучей получаем
(пологие наклонные траектории лучей или присутствие в среде слоистых неоднородностей, вытянутых вдоль оси x), для флуктуации направления распространения лучей получаем
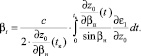 (24)
(24)
Используя формулы (12), (24) для флуктуаций фазы и направления прихода лучевого поля, составим выражения для дисперсий этих характеристик. В частности, для дисперсии фазы в пункте приема имеем
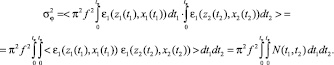 (25)
(25)
Соответственно для дисперсии направления прихода поля:
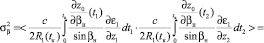
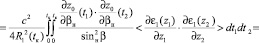
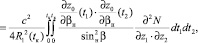 (26)
(26)
где знак < > – означает усреднение по ансамблю неоднородностей среды, 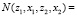
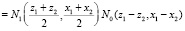 – функция корреляции неоднородностей диэлектрической проницаемости среды. Выражения (25), (26) представляют собой сложные интегралы, поскольку для их вычисления требуется априорная информация о невозмущенной траектории лучевого поля и знание фундаментального решения
– функция корреляции неоднородностей диэлектрической проницаемости среды. Выражения (25), (26) представляют собой сложные интегралы, поскольку для их вычисления требуется априорная информация о невозмущенной траектории лучевого поля и знание фундаментального решения 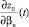 в среде. Однако эти выражения можно эффективно алгоритмизировать. Используя в (25), (26) суммарно-разностное интегрирование [3] и полагая предел tк переменной величиной, интегралы (25), (26) могут быть сведены к системе обыкновенных дифференциальных уравнений первого порядка. Объединяя эту систему с системой невозмущенных лучевых уравнений (13)–(15) (при ε1 = 0), продифференцированной по свободному параметру βн, а также с самой системой (13)–(15) (при ε1 = 0), получаем полную систему дифференциальных уравнений для одновременного расчета средних и среднеквадратичных характеристик фазы и направления прихода лучевого поля в пункте наблюдения:
в среде. Однако эти выражения можно эффективно алгоритмизировать. Используя в (25), (26) суммарно-разностное интегрирование [3] и полагая предел tк переменной величиной, интегралы (25), (26) могут быть сведены к системе обыкновенных дифференциальных уравнений первого порядка. Объединяя эту систему с системой невозмущенных лучевых уравнений (13)–(15) (при ε1 = 0), продифференцированной по свободному параметру βн, а также с самой системой (13)–(15) (при ε1 = 0), получаем полную систему дифференциальных уравнений для одновременного расчета средних и среднеквадратичных характеристик фазы и направления прихода лучевого поля в пункте наблюдения:
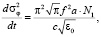
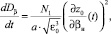
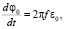
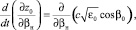
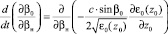 , (27)
, (27)
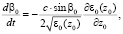
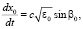
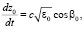
где 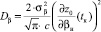 , a – характерный масштаб функции корреляции неоднородностей диэлектрической проницаемости среды.
, a – характерный масштаб функции корреляции неоднородностей диэлектрической проницаемости среды.
Заключение
Предложена схема алгоритмизации решения краевой стохастической задачи электродинамики с использованием численных и аналитических методов. Основу схемы составляет аналитическое решение краевой траекторной задачи для отдельной реализации случайной функции диэлектрической проницаемости среды. Это позволяет исключить проблему пристрелки случайных лучевых траекторий в пункт наблюдения. Получены приближенные соотношения между статистическими траекторными характеристиками поля и параметрами корреляционной функции диэлектрической проницаемости среды. Интегральные выражения для статистических моментов траекторных характеристик преобразованы в системы обыкновенных дифференциальных уравнений первого порядка с начальными условиями. Получена замкнутая система дифференциальных уравнений для расчета траекторных моментов поля в случае квазиоднородного поля неоднородностей среды. Решение системы уравнений допускает численное интегрирование с помощью хорошо апробированных численных методов, таких как, например, Рунге – Кутта, Кутты – Мерсона и др. [1]. Предложенная схема численно-аналитической алгоритмизации решения краевой стохастической задачи позволяет значительно снизить затраты компьютерного времени и допускает включение дифференциальных уравнений для расчета статистических траекторных характеристик лучевых полей, распространяющихся в нестационарных средах, в том числе искусственно возмущенных [5].



