На сегодняшний день область квантовых вычислений постепенно выходит на ведущие позиции в области информационных технологий и вычислительной техники. Все большее внимание ученых и научных исследователей уделяется суперсовременной вычислительной модели, основанной на понятии кубита – квантового бита, призванной вытеснить давно известную модель, нашедшую применение практически во всех средствах вычислительной техники и основанной на понятии бита, которая была разработана Аланом Тьюрингом и Джоном фон Нейманом [1, 2].
Квантовым битом является некая квантовая система, которая до измерения находится в произвольной линейной суперпозиции двух базисных квантовых состояний, а в результате измерения с некоторой вероятностью принимает одно из двух возможных значений. С одной стороны, этот элемент является тем же битом, потому что принимает два значения, а с другой стороны – является квантовым, так как эти два значения находятся в суперпозиции друг с другом [3].
В последнее время квантовая вычислительная модель привлекает к себе все большее внимание ученых и инженеров. Это связано с возможностью её практического применения, что в перспективе даст огромные возможности для решения задач, не нашедших эффективных алгоритмов решения в битовой вычислительной модели.
Одним из ярких примеров таких задач является задача факторизации некоторого числа, решением которой является поиск делителей этого числа [4].
Цель исследования: доказать преимущество квантового алгоритма перед алгоритмами других вычислительных моделей. Как известно, алгоритм Шора имеет квантовую и классическую части, что позволяет увеличить скорость вычисления алгоритма в целом, максимально модернизировав и упростив классическую часть. Несмотря на достоинства квантового алгоритма, он имеет свои недостатки, так как имеет классическую часть, которая выполняется на обычных компьютерах. Именно классическая часть является слабым звеном в алгоритме Шора. И поэтому, модернизировав и максимально упростив её, есть возможность увеличить скорость вычислений квантового алгоритма Шора.
Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA. Более того, система взламывается однозначно, если известен хотя бы один из параметров ключей алгоритма RSA.
ρ-метод факторизации Полларда. Рассмотрим следующий алгоритм:
1. Рассмотрим последовательность целых чисел xn, такую, где каждое следующее число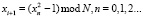 
. В этой последовательности x0 – небольшое число.
2. На каждом шаге будем вычислять значение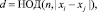 
где j < i.
3. Если d ≠ 1, то вычисления заканчиваются. Найденное число d является делителем числа n. Если n/d не является простым числом, то процедуру можно продолжить, взяв вместо n число n/d.
Главным недостатком данного метода является выделение дополнительной памяти для хранения предыдущих значений xj. Заметим, что если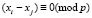 
, то 
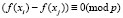. Поэтому, если пара (xi, xj) дает нам решение, то решение даст любая пара 
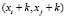[5].
Программная реализация алгоритма ρ-метода факторизации Полларда
}
}
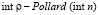
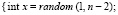
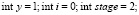
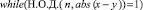
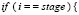
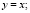
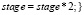
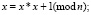
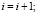
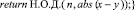
Квантовый алгоритм Шора
Суть данного метода заключается в том, что задача факторизации сводится к задаче поиска периода функции. Когда период функции известен, факторизация осуществляется на классическом компьютере за полиномиальное время при помощи алгоритма Евклида. Квантовой части алгоритма отведено выполнение поиска периода функции. А классическая часть алгоритма сначала специальным образом готовит оную функцию, а потом проверяет найденный квантовой частью период на достаточность для решения задачи. Если период найден правильно (алгоритм вероятностный, так что может найти не то, что хочется), то задача решена. Если же нет, то квантовая часть алгоритма выполняется ещё раз. А поскольку проверка правильности решения для задачи факторизации очень проста (умножили два числа да сравнили с третьим), то эту часть алгоритма вообще можно не принимать во внимание с точки зрения подсчёта сложности [6].
Алгоритм факторизации Шора
1. Выбрать случайное число a, меньшее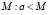 
.
2. Вычислить НОД (a, M). Это может быть сделано при помощи алгоритма Евклида.
3. Если НОД (a, M) не равен 1, то существует нетривиальный делитель числа M, так что алгоритм завершается (вырожденный случай).
4. В противном случае необходимо использовать квантовую подпрограмму поиска периода функции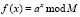 
.
5. Если найденный период r является нечётным, то нужно вернуться на шаг 1 и выбрать другое число a.
6. Если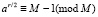 
, то вернуться на шаг 1 и выбрать другое число a.
7. Наконец, определить два значения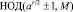 
, которые и являются нетривиальными делителями числа M.
Важным является выбор количества кубитов, которые будут использованы в квантовой схеме. Необходимо выбрать такое количество кубитов q, чтобы выполнялось неравенство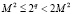 
. При выполнении данного равенства обеспечивается, что данного количества кубитов достаточно, чтобы достаточное количество раз выполнить функцию, для которой ищется период, чтобы сработала конструктивная интерференция [7].
Реализация квантового алгоритма Шора
Перед реализацией необходимо определить некоторые вспомогательные функции и константы.
Константа numberToFactor задаёт число, которое необходимо разложить на простые множители. Константа simpleNumber представляет собой взаимно простое число с предыдущей константой. Далее константы nofAncillas, nofWorkingOubits и nofOubits представляют количество вспомогательных и рабочих кубитов, а также общее количество кубитов в квантовой схеме.
Функция periodicFunction являет собой как раз ту периодическую функцию, задачу поиска периода которой и выполняет квантовая подпрограмма алгоритма Шора.
Далее реализуем квантовую схему в виде функции.
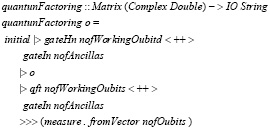
Данное определение соответствует нижеприведенной диаграмме квантовой схемы.
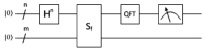
Рис. 1. Диаграмма квантовой схемы
Сравнительный анализ данных алгоритмов на практике
Квантовый алгоритм факторизации Шора, как упоминалось ранее, можно условно разделить на две части – классическую и квантовую. Рассмотрим наиболее слабое место данного алгоритма, а именно классическую часть, которую можно модифицировать и модернизировать.
Классическая часть
В классической части для нахождения НОД предлагается использовать алгоритм Евклида, но, более того, существует достаточно большое количество алгоритмов нахождения наибольшего общего делителя пары чисел. Ниже рассмотрены результаты вычислений каждого из этих алгоритмов, среди которых требуется идентифицировать алгоритм с наименьшей скоростью выполнения поставленной задачи, что позволит квантовому алгоритму в целом работать несколько быстрее, что, в свою очередь, обеспечит больший потенциал для практического применения квантового алгоритма Шора.
В качестве исследуемых отобраны восемь наиболее распространенных алгоритмов нахождения НОД и произведена проверка их скорости вычисления на числах разной сложности. Номерам gcd 1 – gcd 8 соответствуют следующие названия:
1. Перебор от произвольного числа.
2. Перебор от минимального числа.
3. С разложением на делители.
4. Алгоритм Евклида рекурсивный.
5. Алгоритм Евклида итерационный.
6. Бинарный алгоритм рекурсивный.
7. Бинарный алгоритм итерационный.
8. Бинарный алгоритм итерационный со сдвигом.
Результаты вычислений представлены в табл. 1.
Таблица 1
Вычисления классических алгоритмов
|
10–100 |
100–1000 |
1000–10000 |
10000–100 000 |
100 000–1 000000 |
|
|
gcd 1 |
0,0040 |
0,0402 |
0,3531 |
1,7404 |
7,7908 |
|
gcd 2 |
0,0030 |
0,0305 |
0,2490 |
1,3123 |
7,4236 |
|
gcd 3 |
0,0028 |
0,0134 |
0,0436 |
0,1089 |
0,4675 |
|
gcd 4 |
0,0068 |
0,0150 |
0,0273 |
0,0277 |
0,0454 |
|
gcd 5 |
0,0010 |
0,0017 |
0,0025 |
0,0029 |
0,0036 |
|
gcd 6 |
0,0030 |
0,0064 |
0,0085 |
0,0099 |
0,0124 |
|
gcd 7 |
0,0012 |
0,0018 |
0,0020 |
0,0022 |
0,0026 |
|
gcd 8 |
0,0009 |
0,0014 |
0,0016 |
0,0018 |
0,0020 |
Самым эффективным алгоритмом является gcd8 (бинарный с итерационным сдвигом), а gcd 5 (алгоритм Евклида итерационный) является третьим по эффективности.
Наиболее рациональным является выбор алгоритма gcd 8 (бинарный алгоритм итерационный со сдвигом), причиной чему служит то, что он предназначен для решения весьма трудоёмких задач. В связи с этим данный алгоритм вряд ли будет применяться с практической точки зрения для чисел с малым диапазоном, меньших 1000. Рассчитывать среднюю эффективность алгоритма будем по следующей формуле:
. (*)
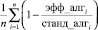Таким образом, использование данного алгоритма в среднем позволит вычислять нахождения НОД двух чисел на 29 % быстрее, чем при использовании стандартного алгоритма Евклида. В алгоритме, при формировании случайного числа а, используется операция генерации случайного числа, которая при вычислении не является достаточно быстрой и кибербезопасной. Поэтому было принято решение заменить эту операцию на n – M, где n < M. Рассчитанный результат средней эффективности алгоритма по формуле (*) составил 72 %. Результаты тестирования этих алгоритмов представлены в табл. 2.
Таблица 2
Вычисления преобразованного алгоритма
|
1–10 |
10–102 |
102–103 |
103–104 |
104–105 |
105–106 |
106–107 |
107–108 |
|
|
random |
0,0019 |
0,0019 |
0,0021 |
0,0021 |
0,0021 |
0,0021 |
0,0021 |
0,0021 |
|
M-n |
0,0005 |
0,0005 |
0,0006 |
0,0006 |
0,0006 |
0,0006 |
0,0006 |
0,0006 |
Стандартная операция возведения в степень также является недостаточно быстрой в данном алгоритме. Проанализировав все существующие алгоритмы, было принято решение использовать алгоритм аддитивных цепочек, средняя эффективность которого, согласно формуле (*), на 53 % выше по сравнению со стандартным алгоритмом. Результаты тестирования алгоритмов представлены в табл. 3.
Таблица 3
Вычисления алгоритма аддитивных цепочек
|
25 |
210 |
220 |
240 |
280 |
2160 |
2320 |
|
|
обычный |
0,0008 |
0,0010 |
0,0014 |
0,0022 |
0,0039 |
0,0072 |
0,0139 |
|
Аддитивные цепочки |
0,0008 |
0,0008 |
0,0009 |
0,0009 |
0,0009 |
0,0009 |
0,0009 |
Произведя модернизацию классической части алгоритма Шора, было произведено тестирование с целью вычисления секретной экспоненты d шифра RSA с ключом в 1024 бита. Результат вычислений с использованием алгоритмов ρ-метода Полларда, стандартного алгоритма Шора и предложенного авторами модифицированного алгоритма Шора представлен на рис. 2.
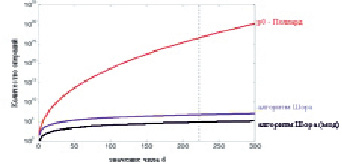
Рис. 2. Сравнение алгоритмов
Исходя из результатов данного эксперимента, наблюдается преимущество предложенного авторами модифицированного квантового алгоритма Шора, модернизированного путем усовершенствования его классической части, которая работает на 50 % быстрее, чем в стандартном алгоритме П. Шора.
Таким образом, сравнивая стандартный и модифицированный авторами алгоритмы Шора и ρ-метод Полларда, можно отметить, что предложенный авторами алгоритм осуществляет процесс обработки данных существенно быстрее. Анализируя график, можно увидеть, что в зависимости от увеличения значения обрабатываемого числа, количество вычислений и затраченное на них время возрастает несущественно.
Заключение
Результаты исследования показывают преимущество квантовых алгоритмов вычислений перед традиционными не квантовыми алгоритмами, вычислительная мощность которых значительно меньше. Оба рассмотренных алгоритма (стандартный и модифицированный) отличаются своей высокой производительностью.
Из рис. 2 видно, что, в зависимости от увеличения значения обрабатываемого числа, количество вычислений и затраченное на них время возрастает несущественно.
Авторам удалось усовершенствовать квантовый алгоритм Шора так, что эффективность полученного алгоритма оказалась выше, чем у стандартного алгоритма, за счет усовершенствования классической части, которая работает на 50 % быстрее.