Автомобильный транспорт является одним из самых удобных видов перевозок. В любой стране состояние автомобильных дорог всегда было и остается важным показателем экономики. Очевидно, что плохие дороги отрицательно влияют на состояние экономики. Важно не только строительство и реконструкция дорог, требующие капитальных затрат, но и проведение комплекса работ и мероприятий по ремонту и содержанию дорог. В работе [1] говорится, что «…экономическая отдача средств, вложенных в ремонт и содержание дорог, в два-три раза превышает экономический эффект от каждого рубля, вложенного в строительство новых дорог». Поэтому оценка состояния дорожно-транспортных сетей и планирование ремонтных работ является важной задачей, имеющей большое экономическое значение в масштабах района, региона, страны.
Огромное количество факторов определяют характер эксплуатации автомобильной дороги. Их необходимо учитывать при организации работ по ремонту и содержанию. Оценка состояния дорог производится с применением программно-аппаратных комплексов, использующих записи видео- камер, видеосъемку, показания систем позиционирования и сканирования, с последующей обработкой результатов наблюдений в автоматизированном режиме. Для решения задачи оценки состояния дорог на базе собранной информации применяются различные подходы, такие как статистические методы [2], машинное обучение [3], кластерный анализ [4] и др.
Другой стороной проблемы является необходимость оптимизировать затраты. Всем российским автомобилистам известно, что данная статья расходов хронически недофинансируется, особенно на уровне региональных и муниципальных дорог. Соответственно, рациональное использование имеющихся ресурсов приобретает ещё большее значение.
В данной работе мы исходим из того, что задача оценки состояния дороги решена с помощью одного из указанных выше подходов, и мы уже имеем карту дефектов дороги, содержащую достаточное количество информации для постановки оптимизационной задачи.
Задачи непрерывной оптимизации работ при ресурсных ограничениях с приложением к ремонту автодорог рассматриваются в работах [5, 6]. Она исследуется с помощью построения ограниченной неотрицательной непрерывной функции f(x,y), характеризующей в каждой точке участка дороги M(x,y) значимость дефекта. Затем решается задача условной минимизации.
В отличие от непрерывного подхода в нашем случае в качестве математической модели применяется дискретная модель комбинаторной оптимизации, заключающейся в поиске оптимального объекта в конечном множестве объектов [7]. В данной статье приводятся содержательная и формальная постановки задачи, рассматривается небольшой пример, показывающий возможности модели, с помощью известного аппарата оценивается сложность задачи и определяются дальнейшие актуальные направления исследований.
Цель исследования, результаты которого изложены в настоящей статье, заключается в разработке дискретной математической модели комбинаторной оптимизации применительно к задаче планирования дорожных ремонтных работ, решение которой позволяет выбрать наиболее дешевый план по критерию общей стоимости ямочного ремонта заданного участка дороги.
Содержательная формулировка задачи и связанные с ней ограничения
Пусть имеется ограниченный по длине и одинаковый по ширине участок дороги с асфальтовым покрытием, для которого известна объективная оценка участка, например, в виде маски дорожного покрытия с указанием границ дефектов и их максимальной глубины [5]. Здесь в качестве дефектов будем рассматривать только выбоины, то есть местные разрушения дорожного покрытия, имеющие вид углублений с резко выраженными краями [1].
Необходимо провести ямочный ремонт данного участка для восстановления его основных качеств. Цитируя [1], в этом случае «…традиционный способ предусматривает обрубку кромок выбоины с приданием ей прямоугольного очертания, очистку ее от асфальтобетонного лома и грязи, подгрунтовку дна и кромок выбоины, заполнение её ремонтным материалом и уплотнение. <…> В качестве ремонтного материала преимущественно используют асфальтобетонные смеси…»
Достаточно часто несколько соседних выбоин вырубаются таким образом, что образуют одну единственную яму прямоугольного очертания, для обозначения которой используется термин «карта ремонта» [1]. Далее мы будем использовать его также и для обозначения ямы, возникающей на месте одной выбоины. Таким образом, карта ремонта – это яма прямоугольного очертания, подготовленная для укладки ремонтного материала после вырубки одной или нескольких соседних выбоин. Будем считать, что стороны любой карты ремонта имеют такую же ориентацию, как и участок дороги, что в основном соответствует практике ремонтных работ.
Кроме того, считаем, что один шаг ямочного ремонта – заделка единой заплатой одной или нескольких соседних выбоин, состоит из двух укрупненных этапов: подготовка карты ремонта и ее заполнение и уплотнение.
Поскольку карта ремонта имеет прямоугольное очертание, так называемая «дорожная заплата» (или просто «заплата»), получаемая в результате заполнения и уплотнения ремонтного материала, – это прямоугольный параллелепипед (кубоид). Если, как в [5], исходить из того, что стоимость заделки ямы пропорциональна объему необходимых для этого работ, то с точки зрения минимизации затрат наиболее рациональным является подход «одна выбоина – одна заплата».
Однако ситуация может измениться, если считать, что стоимость единицы работ первого этапа убывает с увеличением объема заплаты. Иными словами, подготовка двух отдельных выбоин объемом по 1 м3 стоит дороже, чем подготовка одной выбоины объемом 2 м3. При этом будем считать, что стоимость второго этапа, как в [5], пропорциональна объему. В этом случае можно предположить, что за счет удешевления подготовительных работ окажется, что заделывать несколько соседних выбоин одной заплатой будет выгоднее, чем делать на каждую выбоину свою заплату.
Математическая модель, построенная ниже и продемонстрированная на простом примере, показывает, что подобная ситуация вполне реальна. Следовательно, можно говорить о том, что существует некоторое множество планов карт ремонта для заданного участка дороги с известной маской дорожного покрытия, из которых можно выбрать наиболее дешевый план по критерию общей стоимости ямочного ремонта данного участка.
Формализация задачи
Пусть рассматриваемый ограниченный участок дороги является прямоугольником, имеющим длину L и ширину W. Глубина дорожного покрытия в нашем случае не столь важна, чтобы ее определять отдельным символом, поскольку далее будет иметь значение только глубина выбоин. Выбоины представляют собой ограниченные односвязные непересекающиеся множества (не обязательно выпуклые), отделённые друг от друга неповрежденными участками. Пронумеруем все выбоины и будем считать, что их номера представляют собой множество N = {1, 2, …, n}.
Карта ремонта выбоины – это минимальный прямоугольный параллелепипед (кубоид), в который вписывается данная выбоина. Кубоид для выбоины i обозначим C({i}). Уже на этом этапе формальной постановки задачи вместо выбоин можно рассматривать соответствующие им кубоиды. Каждому кубоиду C({i}) можно поставить в соответствие пятерку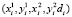 
, где пара 
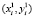– координаты нижнего левого угла четырехугольника карты ремонта на плоскости X-Y (обозначим его R({i})), 
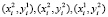– координаты осталь- ных трёх углов в порядке обхода против часовой стрелки, а di – максимальная глубина выбоины. Здесь мы рассматриваем случай, когда 
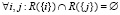(в случае невыполнения этого условия выбоины i и j заранее объединяются в одну). Пример, на котором демонстрируются введенные понятия и обозначения, представлен на рис. 1.
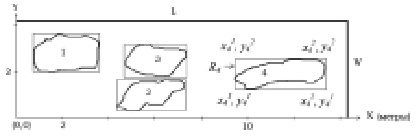
Рис. 1. Пример участка дороги (на плоскости X-Y)
Назовем разбиением множества N такое множество подмножеств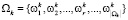 
, каждый элемент которого есть подмножество 
, 
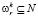и 
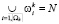. Здесь 
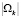означает количество подмножеств ω в разбиении 
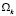, которое может варьироваться от 1 до N. При этом не каждое разбиение является допустимым. Например, на рис. 1 заделке всех выбоин поодиночке соответствует допустимое разбиение 
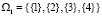, еще одно допустимое разбиение – 
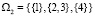, а разбиение 
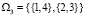не является допустимым, поскольку карты ремонта в этом случае будут накладываться друг на друга. В более общем виде можно записать, что из всего множества разбиений 
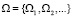множества N разбиение 
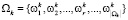является допустимым, если для 
.
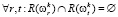Посмотрим, чему равен объем V(ω) для кубоида C(ω), построенного на некотором допустимом подмножестве ω. Если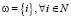 
, то понятно, что 
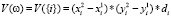. В случае, когда 
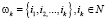, несложно показать, что
.
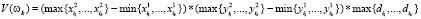Теперь оценим стоимость двух этапов ремонта, а именно подготовки карты ремонта и ее заполнения и уплотнения. Как было отмечено ранее, считаем, что стоимость выполнения единицы объёма первого этапа является функцией, зависящей от объема выполняемых работ: чем больше объём кубоида, тем меньше стоимость единицы работ. Пусть V – вещественный аргумент больше 0, обозначим саму функцию CPre(V). Для CPre(V) из содержательных соображений можно сформулировать следующие свойства:
1. CPre(V) невозрастающая функция: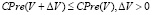 
.
2. CPre(V) ограничена снизу,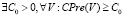 
.
Содержательно C0 означает значение, ниже которого стоимость единицы работ опуститься не может при самых больших объёмах работ. Примерный график CPre(V), который соответствует функции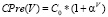 
, где коэффициент 0 < α < 1, приведен на рис. 2.
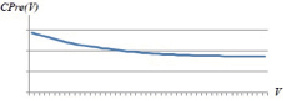
Рис. 2. График функции стоимости выполнения единицы объёма первого этапа
Для второго этапа будем считать, что стоимость заполнения и уплотнения единицы объема не зависит от общего объема выработки; обозначим эту константу CFill. Для заданного разбиения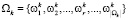 
общая стоимость работ есть функция от разбиения, которая равна
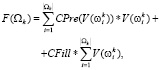
или после незначительных преобразований имеем
.
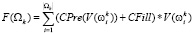Таким образом, на множестве всех допустимых перестановок Ω надо найти перестановку, минимизирующую функцию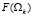 
.
Оптимизационная задача имеет следующую форму (1–2):
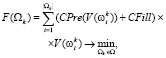(1)
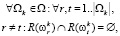(2)
где (1) – целевая функция, а (2) – ограничение на допустимость разбиения.
Пример
Рассмотрим пример, изображенный на рис. 1. Пятерки, соответствующие выбоинам, зададим численно, причем координаты вершин соответствуют изображению на рисунке, а глубину выбоин зададим самостоятельно:
1: (0,7; 2; 3,6; 3,6; 0,2),
2: (4,4; 0,3; 7,2; 1,7; 0,15),
3: (4,5; 1,8; 7,3; 3,3; 0,16),
4: (9,5; 1,2; 13,4; 2,5; 0,3).
Общее количество разбиений множества N = {1,2,3,4} равно 15, но среди них только 7 являются допустимыми. Для конкретных значений (близких к реальным), а именно, CFill = 35000 руб/м3, С0 = 7000 руб/м3, α = 0,6 и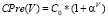 
оптимальное решение достигается при разбиении Ω4 = {{1}, {2,3}, {4}}, стоимость ремонта всего участка при этом равна 48469 руб. Следует поодиночке заделывать выбоины 1 и 4, и одной картой выбоины 2 и 3.
Решение Ω1 = {{1}, {2}, {3}, {4}}, когда все выбоины заделываются поодиночке, стоит 49305 руб.
Решение Ω15 = {{1, 2, 3, 4}, когда все выбоины заделываются одной картой, стоит 1820017 руб.
Некоторые оценки и возможные направления исследований
Число неупорядоченных разбиений n-элементного множества, обозначаемое Bn, называется числом Белла (при этом формально полагают B0 = 1). Для чисел Белла справедлива формула Добинского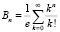 
[8].
Значения первых 15 чисел Белла (начиная с n = 1): 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678 570, 4 213 597, 27 644 437, 190 899 322, 1 382 958 545, то есть решение задачи для 15 выбоин требует более 1,3 млрд операций генерации разбиений.
Естественно, что реальное количество дорожных дефектов гораздо больше, чем 15. Отсюда следуют два возможных взаимосвязанных направления для продолжения исследований:
1) распараллеливание задачи и решение её с использованием высокопроизводительных многопроцессорных [9] и/или грид-систем [10];
2) разбиение задачи на подзадачи, очевидно связанное с тем, что достаточно протяженный участок дороги может быть разбит на несколько участков, следующих один за другим.
Одним из возможных математических подходов здесь представляется последовательная кластеризация объектов на плоскости с заданным количеством кластеров (или объектов, попадающих в каждый кластер), что, в свою очередь, приводит к интересной оптимизационной задаче.
Заключение
В статье рассмотрены содержательная и формальная постановки задачи ямочного участка дороги, сформулированная в виде задачи комбинаторной оптимизации разбиения множества на непересекающиеся подмножества, и дающей оптимум в смысле минимальных затрат ресурсов на ремонт заданного участка. Подробно рассматривается пример, показывающий адекватность и возможности модели. С помощью чисел Белла оценивается сложность задачи, близкая к экспоненциальной, и определяются дальнейшие направления исследований, связанные с использованием высокопроизводительных вычислителей и разбиением задачи на подзадачи.