Проблема управления качеством образования как сложной слабоформализуемой системы связана с высоким темпом социальных, экономических процессов, изменяющихся требований рынка труда и т.д. Для принятия решений по управлению в условиях неопределённости может применяться универсальный инструментарий моделирования сложных систем – когнитивные карты (КК), которые задаются в виде ориентированного графа и содержат двухуровневые значения связей между концептами. Расширением традиционных КК является аппарат нечетких когнитивных карт (НКК), предложенных Б. Коско [1, 2], в которых причинно-следственные связи между концептами находятся в диапазоне действительных чисел [–1, 1].
Для поддержки принятия решений по управлению качеством образования применяется математический аппарат НКК В.Б. Силова [3], обеспечивающий комплексный анализ причинно-следственных связей между концептами и предназначенный для определения совокупного взаимовлияния концептов друг на друга с учётом прямого и опосредованного влияния. Когнитивный анализ необходим для принятия решений по выбору наилучших путей достижения целевых индикаторов качества образования и с целью повышения эффективности использования направленных на повышение качества образования бюджетных средств.
Материалы и методы исследования
На основе статистических данных, предоставленных Федеральной службой государственной статистики [4], о качестве образования в регионах РФ за 2015/2016 гг. разработана [5, 6] НКК качества образования (рис. 1). Когнитивная карта содержит концепты системы образования, разделенные на целевые, управляющие и промежуточные; оценка связей между концептами проведена методами статистического и интеллектуального анализа.
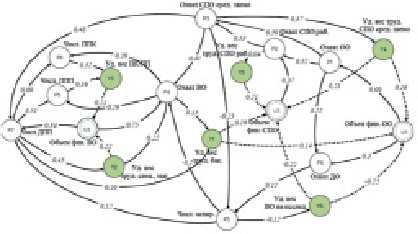
Рис. 1. Нечеткая когнитивная карта качества образования
Целевыми концептами НКК качества образовательной системы являются: удельные веса трудоустроившихся выпускников образовательных организаций по программам бакалавриата 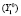 , высшего образования – специалитет, магистратура
, высшего образования – специалитет, магистратура 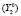 ; среднего профессионального образования (подготовка квалифицированных рабочих, служащих)
; среднего профессионального образования (подготовка квалифицированных рабочих, служащих) 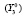 ; среднего профессионального образования (подготовка специалистов среднего звена)
; среднего профессионального образования (подготовка специалистов среднего звена) 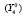 ; удельный вес численности занятого населения в возрасте 25–65 лет, прошедшего повышение квалификации и (или) профессиональную подготовку
; удельный вес численности занятого населения в возрасте 25–65 лет, прошедшего повышение квалификации и (или) профессиональную подготовку 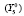 ; удельный вес сектора учреждений высшего образования во внутренних затратах на исследования и разработки
; удельный вес сектора учреждений высшего образования во внутренних затратах на исследования и разработки 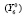 .
.
Внутренние концепты НКК характеризуют: охват детей начальным общим, основным общим и средним общим образованием (7–17 лет) (P1); охват молодежи образовательными программами среднего профессионального образования – программами подготовки квалифицированных рабочих, служащих (15–17 лет) (P2), программами подготовки специалистов среднего звена (15–19 лет) (P3); охват молодежи образовательными программами высшего образования (17–25 лет) (P4); численность аспирантов на 100 студентов (P5); охват детей в возрасте от 5 до 18 лет программами дополнительного. образования (P6); численность лиц, обученных в организации по дополнительным профессиональным программам, на 10 тыс. человек (P7), по программам повышения квалификации на 10 тыс. чел. (P8), по программам профессиональной переподготовки на 10 тыс. чел. (P9).
Управляющими концептами, направленными на повышение качества образования, являются объемы финансирования образовательных организаций (в тыс. руб/чел.): общий объем финансирования всех образовательных организаций, реализующих программы общего образования (U1), объем финансирования образовательных организаций высшего образования (U2); объем поступивших средств в среднее профессиональное образование (U3).
В математическом виде НКК представляется в виде матрицы смежности W = [wij]nxn, элементы которой отмечают степень влияния концепта i на концепт j в диапазоне действительных чисел [–1, 1] с учетом направления влияния. Дальнейший анализ НКК качества образования проводится по схеме алгоритма В.Б. Силова, показанной на рис. 2.
Результаты исследования и их обсуждение
Согласно схеме алгоритма анализа НКК качества образования на первом шаге формируется квадратная матрица смежности W, представленная в табл. 1. Размерность матрицы определена общим количеством концептов (n = 18); элементы матрицы представляют собой степень влияния концепта-причины, расположенного в строке, на концепт-следствие в столбце.
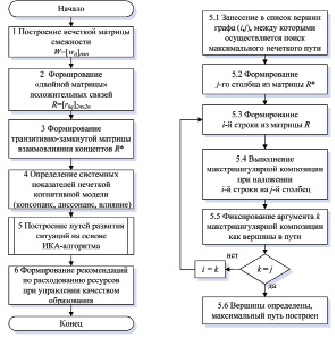
Рис. 2. Схема алгоритма проведения анализа нечеткой когнитивной модели
Таблица 1
|
W |
U1 |
U2 |
U3 |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P7 |
P8 |
P9 |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
|
U1 |
0,09 |
0,3 |
||||||||||||||||
|
U2 |
0,75 |
0,34 |
||||||||||||||||
|
U3 |
0,37 |
|||||||||||||||||
|
P1 |
0,52 |
0,5 |
0,22 |
0,42 |
0,57 |
0,29 |
0,42 |
0,31 |
||||||||||
|
P2 |
0,33 |
0,27 |
0,04 |
0,26 |
0,19 |
|||||||||||||
|
P3 |
0,41 |
–0,23 |
0,48 |
0,34 |
0,55 |
0,31 |
0,37 |
|||||||||||
|
P4 |
0,39 |
0,29 |
0,13 |
0,22 |
0,19 |
0,18 |
0,18 |
|||||||||||
|
P5 |
–0,2 |
0,12 |
–0,12 |
|||||||||||||||
|
P6 |
0,12 |
0,24 |
0,29 |
|||||||||||||||
|
P7 |
0,99 |
0,51 |
0,16 |
0,43 |
0,26 |
0,35 |
||||||||||||
|
P8 |
0,32 |
|||||||||||||||||
|
P9 |
0,16 |
|||||||||||||||||
|
Y1 |
0,14 |
0 |
0,19 |
|||||||||||||||
|
Y2 |
0,17 |
0,22 |
0,23 |
|||||||||||||||
|
Y3 |
0,2 |
0,21 |
||||||||||||||||
|
Y4 |
0,16 |
0,2 |
0,21 |
|||||||||||||||
|
Y5 |
0,21 |
|||||||||||||||||
|
Y6 |
–0,25 |
–0,22 |
На следующем шаге на основе матрицы смежности W формируется «двойная матрица» R = [rkq]2n×2n положительных связей. Необходимость построения матрицы R обусловлена требованиями методов нечеткой алгебры – введением нечеткости в диапазоне действительных чисел [0, 1] и связанной с исключением отрицательных элементов. Каждый элемент «двойной» матрицы определяется следующим образом: если соответствующий элемент матрицы смежности wij > 0, то 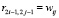 ,
, 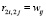 ; если wij < 0, то
; если wij < 0, то 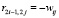 ,
, 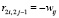 , в остальных случаях элементы матрицы R равны нулю. В табл. 2 представлен фрагмент «двойной матрицы» R, описывающей влияние промежуточных концептов НКК качества образования P2, P3, P4, P5 друг на друга; элементы матрицы смежности W расщепляются в R на две строки cледующим образом: положительные элементы записываются по главной диагонали, например, P2 – P3, P2’ – P3’, а отрицательные элементы – по побочной диагонали, например, P3 – P5’, P3’ – P5.
, в остальных случаях элементы матрицы R равны нулю. В табл. 2 представлен фрагмент «двойной матрицы» R, описывающей влияние промежуточных концептов НКК качества образования P2, P3, P4, P5 друг на друга; элементы матрицы смежности W расщепляются в R на две строки cледующим образом: положительные элементы записываются по главной диагонали, например, P2 – P3, P2’ – P3’, а отрицательные элементы – по побочной диагонали, например, P3 – P5’, P3’ – P5.
Таблица 2
|
R |
P2 |
P2’ |
P3 |
P3’ |
P4 |
P4’ |
P5 |
P5’ |
|
P2 |
0 |
0 |
0,33 |
0 |
0 |
0 |
0 |
0 |
|
P2’ |
0 |
0 |
0 |
0,33 |
0 |
0 |
0 |
0 |
|
P3 |
0 |
0 |
0 |
0 |
0,41 |
0 |
0 |
0,23 |
|
P3’ |
0 |
0 |
0 |
0 |
0 |
0,41 |
0,23 |
0 |
|
P4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
P4’ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
P5 |
0 |
0 |
0 |
0 |
0 |
0,2 |
0 |
0 |
|
P5’ |
0 |
0 |
0 |
0 |
0,2 |
0 |
0 |
0 |
Таблица 3
|
R* |
Y4 |
Y5 |
Y6 |
|||
|
U1 |
0,01665 |
–0,00003 |
0,01349 |
–0,00123 |
0,00124 |
–0,00432 |
|
U 2 |
0,00166 |
0,00000 |
0,26386 |
–0,00005 |
0,00012 |
–0,00009 |
|
U 3 |
0,04518 |
–0,00005 |
0,03192 |
–0,00134 |
0,00337 |
–0,00003 |
|
P1 |
0,18500 |
–0,00019 |
0,13071 |
–0,00640 |
0,01380 |
–0,00317 |
|
P2 |
0,12210 |
–0,00013 |
0,08627 |
–0,00363 |
0,00911 |
–0,00008 |
|
P3 |
0,37000 |
–0,00039 |
0,26142 |
–0,01100 |
0,02760 |
–0,00026 |
|
P4 |
0,00142 |
0,00000 |
0,17120 |
–0,00004 |
0,00011 |
–0,00008 |
Для определения опосредованного влияния всех концептов НКК качества образования друг на друга строится транзитивно-замкнутая матрица взаимовлияний концептов 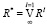 , состоящая из положительно-отрицательных пар элементов, характеризующих максимальные положительные и отрицательные причинно-следственные пути между всеми концептами [7]. Матрица взаимовлияний R* формируется по специальному правилу преобразования: (
, состоящая из положительно-отрицательных пар элементов, характеризующих максимальные положительные и отрицательные причинно-следственные пути между всеми концептами [7]. Матрица взаимовлияний R* формируется по специальному правилу преобразования: (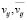 ): vij = max
): vij = max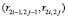 ,
, 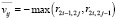 . Построенная матрица взаимовлияний R* позволяет определить согласованные отношения взаимовлияния всех концептов НКК качества образования, что может быть использовано для анализа динамики достижения заданных целей качества образования. Следует отметить, что для осуществления процедуры транзитивного замыкания требуется введение в НКК обратных связей по управлению, показанных на рис. 1 штриховыми линиями.
. Построенная матрица взаимовлияний R* позволяет определить согласованные отношения взаимовлияния всех концептов НКК качества образования, что может быть использовано для анализа динамики достижения заданных целей качества образования. Следует отметить, что для осуществления процедуры транзитивного замыкания требуется введение в НКК обратных связей по управлению, показанных на рис. 1 штриховыми линиями.
Фрагмент полученной замкнутой матрицы взаимовлияний R* представлен в табл. 3, в которой показано, что, например, при росте объема финансирования общего образования U2 несколько увеличивается целевой показатель качества образования Y5 – удельный вес численности занятого населения в возрасте 25–65 лет, прошедшего повышение квалификации и (или) профессиональную подготовку и т.д. Дальнейший анализ матрицы R* показал, что изменения вложений бюджетных средств образовательных организаций, реализующих программы общего образования U1 и среднего профессионального образования U3, не оказывают существенного влияния на целевые концепты, а рост вложений U2 оказывает влияние на целевые концепты Y1, Y2, Y5.
По построенной матрице взаимовлияния можно провести расчет системных показателей НКК [5, 8]: интегральные показатели консонанса (диссонанса) влияния системы образования на концепт, консонанса (диссонанса) влияния концепта на систему, а также показатели, нормированные к сумме всего консонанса (диссонанса) системы. Анализ интегральных системных показателей НКК выявил высокий уровень консонанса, т.е. высокую степень согласованности концептов когнитивной модели, и низкую степень диссонанса.
Далее применяется алгоритм В.Б. Силова, необходимый для поиска путей по матрице взаимовлияния между концептами; данный алгоритм играет роль интеллектуального когнитивного агента (ИКА-алгоритм). Выявленные с помощью алгоритма пути между концептами рассматриваются как возможные пути использования бюджетных средств для улучшения качества образования и могут служить основой для формирования рекомендаций по принятию решений при управлении.
Согласно ИКА-алгоритму для определения максимального позитивного и негативного пути между концептами необходимо из построенной матрицы взаимовлияний R* выделить (занести в список) номера вершин между концептами, для которых требуется найти максимальный «по весу» нечеткий путь. Для этого в матрице R* фиксируется j-й столбец y, а в матрице R формируется i-я строка s. После этого значение аргумента макстриангулярной композиции вектора-строки s и вектора-столбца y нечетких матриц R* и R фиксируется как вершина k в пути. Следует отметить, что макстриангулярные операции с нечеткими матрицами предполагают, что нечеткие значения выходных концептов рассчитываются с использованием характерных для нечеткой логики операций T- и S-норм над нечеткими значениями входных концептов (например, с использованием правила max–product). Процесс поиска путей ИКА-алгоритмом продолжается до тех пор, пока фиксированная вершина k не совпадет с j-й вершиной. На рис. 3 приведен фрагмент процедуры извлечения номеров вершин путей с помощью ИКА-алгоритма.
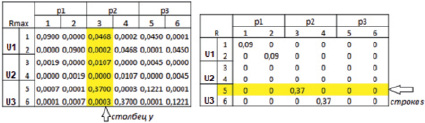
Рис. 3. Фрагмент процедуры извлечения номеров вершин в ИКА-алгоритме
ИКА-алгоритм позволяет построить пути развития ситуации при задании управляющих воздействий, необходимых для повышения качества образования. В качестве примера рассмотрим максимальные позитивный и негативный пути между концептами U2 – «Объем финансирования образовательных организаций высшего образования, тыс. руб/чел.» на концепт Y2 – «Удельный вес трудоустроившихся выпускников образовательных организаций по программе высшего образования – специалитет, магистратура»; по матрице взаимовлияний значения отношения между концептами U2 и Y2 соответствуют величинам (0,165; –0,00003). Позитивное влияние U2 на Y2 проходит по НКК через концепты (U2, P4, Y2): 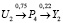 , т.е. управляющий концепт увеличивает промежуточный концепт P4 «Охват молодежи образовательными программами высшего образования», что приводит к увеличению целевого концепта Y2. Негативное влияние концепта U2 на Y2 проходит по более протяженному маршруту (X2, P4, Y1, U3, P2, P3, P5, P7, Y2):
, т.е. управляющий концепт увеличивает промежуточный концепт P4 «Охват молодежи образовательными программами высшего образования», что приводит к увеличению целевого концепта Y2. Негативное влияние концепта U2 на Y2 проходит по более протяженному маршруту (X2, P4, Y1, U3, P2, P3, P5, P7, Y2): 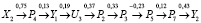 , в котором управляющий концепт U2, повышая промежуточный концепт P4, увеличивает один из целевых концептов Y1 и вносит изменения в управляющий концепт U3; увеличение управляющего концепта U3, в свою очередь, положительно влияет на состояние системы образования, так как увеличивает промежуточные концепты P2, P3, но при этом происходит уменьшение концептов P5, P7, вследствие этого снижается и целевой концепт Y2 – «Удельный вес трудоустроившихся выпускников образовательных организаций по программе высшего образования – специалитет, магистратура». Таким образом, проведение когнитивного анализа построенной НКК на основе алгоритма В.Б. Силова позволяет найти возможные пути влияния управляющих концептов на целевые концепты и сформировать рекомендации по расходованию бюджетных средств при управлении качеством образования.
, в котором управляющий концепт U2, повышая промежуточный концепт P4, увеличивает один из целевых концептов Y1 и вносит изменения в управляющий концепт U3; увеличение управляющего концепта U3, в свою очередь, положительно влияет на состояние системы образования, так как увеличивает промежуточные концепты P2, P3, но при этом происходит уменьшение концептов P5, P7, вследствие этого снижается и целевой концепт Y2 – «Удельный вес трудоустроившихся выпускников образовательных организаций по программе высшего образования – специалитет, магистратура». Таким образом, проведение когнитивного анализа построенной НКК на основе алгоритма В.Б. Силова позволяет найти возможные пути влияния управляющих концептов на целевые концепты и сформировать рекомендации по расходованию бюджетных средств при управлении качеством образования.
Заключение
Проведен когнитивный анализ НКК качества образования на основе алгоритма В.Б. Силова; построены: матрица смежности, «двойная матрица» положительных связей, сформирована транзитивно замкнутая матрица взаимовлияния концептов НКК друг на друга, определены максимальные позитивные и негативные пути достижения целевых концептов из управляющих концептов. Построенные пути являются основой для формирования цепочки нечетких правил вида «если – то» и могут использоваться для формирования рекомендаций по принятию решений при управлении качеством образования.
Работа выполнена при поддержке гранта РФФИ № 17-08-01155 А «Интеллектуальная поддержка принятия решений при управлении многоотраслевым производственным комплексом как многосвязным динамическим объектом на основе нейросетевого и имитационного моделирования».



