В настоящее время в системе обучения учащихся с особыми образовательными потребностями активно используются дистанционные технологии. Особенно они активно используются для обеспечения дополнительного образования наряду с традиционной формой обучения. В результате активного применения данных технологий в педагогической науке возникли дополнительные разделы методики, касающиеся дистанционной формы обучения. Но, несмотря на это, методика дистанционного обучения еще только строится, и в этом вопросе наметились определенные проблемы, особенно это касается физико-математического обучения и, в частности, преподавания математики в 5 классе. Использование традиционных форм обучения математике в пятом классе на основе дистанционных технологий в большинстве случаев не дает необходимого результата, поэтому необходима разработка современных методических аспектов к осуществлению дистанционного обучения математике в пятом классе.
Цель исследования: рассмотрение методических особенностей разработки универсального электронного курса по математике для учащихся 5-х классов с особыми образовательными потребностями.
Материалы и методы исследования
Основой построения дистанционного курса по математике для 5-х класса являются идеи развивающего обучения, предложенные российскими педагогами-новаторами Л.С. Выготским, Л.В. Занковым и др. Смысл основной концепции развивающего обучения – это основополагающая роль теоретических знаний, основная цель которых в осознанном изучении теоретических знаний обучающимися, а потому его воплощение заключается в том, что ученик, выполняя упражнения в заданной последовательности, вырабатывает способность самостоятельно формулировать правила, давать определение неизученного или уже знакомого понятия или даже предложить новый термин [1].
Разработанный дистанционный курс содержит весь комплекс вопросов, изучаемых в 5-м классе, но в связи с тем, что в настоящее время существует большой перечень учебников, по которым обучаются, и педагоги дополнительного образования должны подстраиваться под знания и желания учащихся, поэтому одной из задач разработанного курса была его универсальность. Данная концепция предполагает включение всех дополнительных вопросов, отраженных в учебниках разных авторов. Кроме того, учащиеся выбирают количество часов на изучение предмета, поэтому универсальность курса помогает решить и эту проблему.
Разработанный дистанционный курс предполагает представление материала в нескольких вариантах сложности, при этом теоретический материал для каждого уровня сложности представлен одинаково. Отличия заключаются в выборе задач для решения и проверочных работ. В результате учителю дана возможность подобрать нужный ему материал в зависимости от выбранной учащимся сложности изучения и количества часов.
При разработке учебного курса отдельное внимание было уделено формированию теоретического материала по предмету [2]. Поскольку учащиеся пятого класса еще относительно небольшого возраста, изложение теории иллюстрируется красочными рисунками, объяснение сопровождается мультипликационными роликами, каждое действие алгоритма работы, например с дробями, выделяется собственным цветом. Различные сложные моменты теории объясняются несколько раз с задействованием различных видов памяти на основе жизненных ситуаций, тем самым учащимся демонстрируется связь математики с жизнедеятельностью человека, чтобы у них не формировалось мнение, что математические знания не нужны в жизни.
В теории также разбираются основные задачи каждой темы. Алгоритм решения поясняется с использованием изображений сказочных героев, таких как Незнайка, Красная шапочка, Карлсон и др., при этом герои задают учащемуся наводящие вопросы, на которые сами и отвечают через некоторое время, указывая на то, что учащийся и сам так думал. Использование такого принципа изложения материала способствует росту интереса у учащихся, а также формирует позитивную атмосферу для проведения урока [3].
Каждый урок содержит и материалы, необходимые для проверки теоретических и практических знаний учащихся. Проверка теоретических знаний представлена тестами двух уровней. Первый уровень содержит вопросы по теории, на которые даны варианты ответов, и учащийся должен выбрать из них только один правильный, об этом ему сообщается в начале теста. Второй уровень является более сложным и предполагает вопросы с несколькими правильными ответами, вопросы, требующие вводить ответ с клавиатуры, к тому же вопросы подобраны более сложные.
Третью часть любого урока составляют практические задания для решения совместно с учителем, самостоятельного решения и домашнее задание. Задания для самостоятельного решения и домашнее задание также представлены несколькими уровнями сложности для обеспечения целостности концепции изучения предмета. Подбор домашнего задания и задач для самостоятельного решения особой проблемы при разработке дистанционного курса не вызвал.
Наибольшую проблему при разработке универсального курса по математике для пятого класса представляют собой задачи для совместного решения с учителем на уроке. Проблема состоит не в подборе самих заданий, а в обеспечении наглядности и взаимодействия учителя и ученика в процессе решения задачи. При дистанционном обучении, к сожалению, нет возможности вызвать учащегося к доске и, подсказывая ученику, получить совместное решение задачи [4].
Для решения данной проблемы по организации взаимодействия учителя и учащегося в каждом уроке курса разработаны задания диалогового типа с подключением интерактивной доски. Данное программное обеспечение широко представлено в сети Интернет. Диалоговые задания представлены тремя уровнями. Задания первого уровня представляют собой поэтапное решение задачи, но наиболее сложные и трудные моменты решения уже представлены, а учащийся под руководством учителя добавляет недостающие компоненты решения. Такие задания не требуют высокой предметной подготовки учащегося. Задания второго уровня содержат задачи, в которых уже указаны незначительные и самые легкие моменты решения, а вот наиболее трудные моменты решения должен дописать учащийся при помощи учителя. Если у учащегося возникли проблемы на каком-то этапе решения, то он с разрешения учителя может нажать на подсказку сказочного героя и получить не сам этап решения, а только ценный совет, позволяющий направить его мысли на правильное решение. Кроме того, учителю дается доступ к сложным компонентам решения задачи, спрятанным от ученика. Для этого используется технология слоев, которой обладают почти все интерактивные доски. В нужный момент учитель может сделать слой активным, и учащийся познакомится с этапом решения задачи. Доступ к сложным моментам решения можно организовывать постепенно, что будет способствовать развитию мыслительной деятельности учащегося.
Задания третьего уровня также представляют собой поэтапное решение задачи с указанием несложных компонентов решения, но уже никаких подсказок не предусмотрено. Учителю не предоставляется доступа к сложным моментам решения задачи в ходе урока, единственное, что может учитель и ученик – это вносить записи в решение. Такие задания требуют от учителя высокой предметной подготовки и необходимости самостоятельно перед уроком просмотреть данные задачи. В остальном разработанный универсальный курс значительно облегчает деятельность учителя и нет необходимости подбирать учебный материал с соответствующими презентациями, материалы для проверки знаний и домашнего задания, а также быть привязанным к определённому учебнику [5].
Особое внимание уделено геометрическим вопросам, изучаемым в пятом классе. Это связано с тем, что накопленные знания на данном этапе имеют важное значение при изучении систематического курса геометрии. Значительная часть материала изучается и усваивается учащимися только на уровне представлений, поэтому особое внимание необходимо уделить вопросу обеспечения наглядности изучаемого материала.
При проектировании геометрических заданий предлагается разработка к каждой задаче поэтапных чертежей, выполненных в цвете. Каждая новая операция при решении задачи иллюстрируется на чертеже другим цветом, что обеспечивает наглядность каждого этапа решения. Сами чертежи можно разработать с помощью различных графических программ, но после этого чертежи должны быть представлены в виде документа для интерактивной доски. Интерактивная доска позволяет вносить записи в решение учащемуся и учителю одновременно, дорисовывать чертежи. Диалоговые геометрические задания входят в основу авторского дистанционного курса и позволяют обеспечить дистанционному обучению принципиально новый методический уровень.
Результаты исследования и их обсуждение
Эффективность разработанного универсального дистанционного курса была подтверждена в ходе педагогического эксперимента. В эксперименте участвовали 44 ученика 5 класса дистанционного центра и 6 учителей математики. Целью эксперимента была оценка уровня полученных знаний учащимися 5 классов при использовании разработанного курса в сравнении с результатами обучения по стандартной методике, а также рост уровня интереса к предмету. Для осуществления эксперимента обучающихся поделили на две группы, первая группа курс математики пятого класса осваивала обычными методами с использованием разработанных учителями материалов и обычных учебников, а преподавание во второй группе осуществлялось на основе разработанного универсального курса. В экспериментальных группах, для чистоты эксперимента, были подобраны ученики, указавшие в индивидуальном плане разное количество часов математики в неделю и различный по сложности уровень подготовки. Учителя, принимавшие участие в эксперименте, проводили уроки на основе традиционной методики и с использованием разработанного курса, таким образом, педагог работал с учениками из первой и второй группы. Эксперимент проводился в течение двух лет с двумя параллелями учащихся.
Для обеспечения достоверности результатов эксперимента была проведена проверка знаний учащихся с использованием различного уровня контрольных, тестов и срезов знаний, представленных независимыми педагогами других учебных заведений и департаментом образования области.
Для оценки результатов педагогического эксперимента можно представить следующие уровни формирования знаний и умений [6] у учащихся 5 классов:
– 3 уровень – учащиеся автоматизированно, свернуто и безошибочно выполняют математические действия (80–100 %),
– 2 уровень – учащиеся умеют достаточно свободно выполнять математические действия, осознавая каждый шаг (60–80 %),
– 1 уровень – учащиеся умеют выполнять математические действия самостоятельно, но лишь по образцу (40–60 %);
– 0 уровень – учащиеся совершенно не владеют знаниями и умениями (менее 40).
На основе представленных уровней были получены контрольные результаты в обеих группах:
В контрольной группе, проходившей обучение по обычной программе, получены результаты, изображенные на рис. 1.
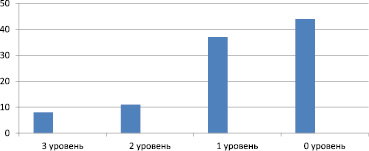
Рис. 1. Уровень формирования знаний и умений в контрольной группе
– 3 уровень – 8 %;
– 2 уровень – 11 %;
– 1 уровень – 37 %;
– 0 уровень – 44 %.
В экспериментальной группе, обучавшейся с использованием разработанного курса, получены результаты, отображенные на рис. 2.
– 3 уровень – 21 %;
– 2 уровень – 34 %;
– 1 уровень – 36 %;
– 0 уровень – 9 %.
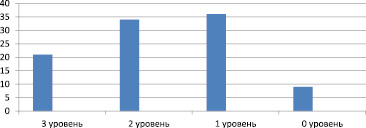
Рис. 2. Уровень формирования знаний и умений в экспериментальной группе
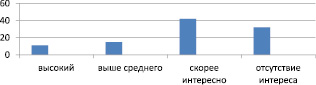
Рис. 3. Уровень интереса к предмету в контрольной группе

Рис. 4. Уровень интереса к предмету в экспериментальной группе
Полученные результаты свидетельствуют, что применение универсального дистанционного курса по математике повысило уровень сформированных [7] знаний и умений у учащихся, что показывает положительный эффект разработанного материала.
Вторым параметром оценки эксперимента показывался интерес у учащихся к предмету. Для оценки интереса были выделены следующие критерии:
– высокий интерес (90–100 %),
– интерес выше среднего (70–90 %),
– скорее интересно, чем нет (40–70 %);
– отсутствие интереса (менее 40).
В контрольной группе, обучавшейся по обычной программе, получены результаты, представленные на рис. 3.
– высокий интерес – 11 %;
– интерес выше среднего – 15 %;
– скорее интересно, чем нет – 42 %;
– отсутствие интереса – 32 %.
В экспериментальной группе получены результаты, представленные на рис. 4.
– высокий интерес – 27 %;
– интерес выше среднего – 38 %;
– скорее интересно, чем нет – 23 %;
– отсутствие интереса – 12 %.
Представленные результаты демонстрируют рост интереса к предмету в экспериментальной группе.
Заключение
Таким образом, можно утверждать, что разработанный нами универсальный дистанционный курс по математике для пятого класса позволит в полной мере использовать преимущества дистанционных технологий обучения, а также повысит качество обучения не только при дополнительном обучении математике детей с особыми образовательными потребностями, но и при использовании данного материала в обычном образовательном процессе.
Работа выполнена при поддержке гранта РФФИ № 17-16-67015-ОГН и Администрации Смоленской области.



