В научных исследованиях используются различные технологии, в том числе компьютерное моделирование. Большое значение имеет выбор подходящих методов и подходов при решении конкретных задач. Например, в физике плазмы широко используется подход, основанный на применении численных методов при решении уравнений магнитной гидродинамики.
Одним из перспективных направлений таких исследований стал учет различных физических и технологических факторов при постановке и численного решения задач динамики выбросов плазмы на Солнце. Этот класс задач, несмотря на его значимость, мало исследован, что связано, прежде всего, со значительными трудностями в построении алгоритмов их решения. Применение новых технологий разработки программ, использующих современный аппарат математического моделирования, способствует достижению высоких технологических показателей и повышению критерия качества решения.
В конкретных ситуациях, при выборе технологии численного решения важно учитывать те или иные физические эффекты магнитной гидродинамики, а именно вязкость, теплопроводность и электрическое сопротивление плазмы, а также правильно подбирать начальные и граничные условия.
В настоящей работе рассматриваются задачи о распространении облаков плазмы в межпланетном магнитном поле, задаются определенные конфигурации магнитного поля и начальных условий. Обсуждаются различные подходы к её решению, в том числе и технологические.
Материалы и методы исследования
Для решения системы уравнений идеальной магнитной гидродинамики использовался численный метод – схема WENO (weighted essentially non-oscillatory). WENO-схема базируется на локальном характеристическом разложении волн. Во-первых, потоки разделяются в каждом семействе волн. Затем они дробятся в положительной и отрицательной частях по глобальному или локальному делению потока Лакса – Фридрихса. Впоследствии потоки на границах ячеек создаются по WENO-аппроксимации.
Теоретические исследования динамики корональных выбросов массы (КВМ), как крупномасштабного явления, обычно проводятся в приближении магнитной гидродинамики. Проблема гидродинамического описания здесь осложняется необходимостью учета структуры магнитного поля, которая в большинстве случаев не является очевидной. В связи с тем, что постановка задачи о моделировании КВМ не является однозначной ни с физической, ни с математической точки зрения особенно важен выбор технологического подхода. Поэтому задача определения технологических показателей численного решения делает актуальной проблему построения соответствующих математических моделей, выбора подходящего технологического критерия качества, а также разработки численных методов решения соответствующих задач.
История наблюдений КВМ насчитывает около полувека, однако использование в последнее время различных новых технических средств позволило получить большое количество подробных данных, из которых можно сделать ряд заключений о характере этого явления. Отдельной важной проблемой является описание механизма запуска КВМ, которое здесь мы не затрагиваем. Наша задача – показать существующие возможности технологии МГД-моделирования для объяснения основных наблюдаемых свойств КВМ. С этой точки зрения удобно выбрать кинематические параметры явления – скорость и ускорение.
Оценки видимой скорости ядер КВМ дает значения от 20 до 1500 км/с, случаи больших скоростей существуют, но редки [1] (рис. 1). Кинематическая классификация позволяет разделить КВМ на медленные и быстрые, причем первые имеют тенденцию к ускорению (рис. 2), по крайней мере, в поле видимости коронографа, вторые – к замедлению [1–2]. Подобное усреднение скоростей объясняется действием потока солнечного ветра, среднее значение которого находится около 400 км/с.
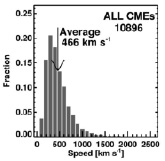
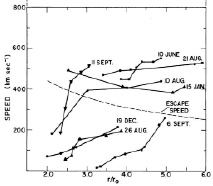
Рис. 1. Распределение КВМ по скоростям [1]
Рис. 2. Изменение скорости КВМ с расстоянием от Солнца [2]
Одним из часто обсуждаемых вопросов, связанных с изучением возникновения и динамики КВМ, является роль магнитного пересоединения. В настоящее время принято считать, что вспышки, эрупция протуберанцев и КВМ есть составные части единого процесса глобальной магнитной эрупции. Согласно стандартной модели вспышки/КВМ, магнитное пересоединение играет ключевую роль на начальной стадии эрупции, когда процесс развивается в нижних, относительно плотных областях короны.
В обзоре [3] подробно проанализированы кинематические свойства 6621 событий, наблюдавшихся при помощи SOHO/LASCO. Замедленное движение (DD CME) оказалось далеко не характерным для их динамики и наблюдалось только в 1797 из рассмотренных случаев, в то время как в 2132 случаях наблюдалось ускорение (AA CME). Наблюдалось также движение со знакопеременным ускорением: ускорение с последующим замедлением (AD CME, 1482 случая) и даже замедление с последующим ускорением (DA CME, 1210 случаев). Обозначена корреляция кинематических свойств с условиями возникновения КВМ: тип AA наблюдается перед вспышками, тип DD – после вспышек, в других случаях подобная корреляция не очевидна.
Подобная статистика свидетельствует о неоднозначности в целом динамики КВМ и существовании множества факторов, приводящих к этому результату. Механизм их распространения в гелиосфере так же до конца не понят, как и механизм начального ускорения. На распространение могут оказывать влияние как солнечный ветер (аэродинамическое торможение), так и ударная волна, возникающая впереди самого облака КВМ [4].
Адекватное моделирование процесса распространения КВМ до расстояний в несколько десятков R? является существенно трехмерной задачей, которая требует для своего решения солидных технических и программных ресурсов. В последние годы оно становится доступным для широкого круга исследователей, что объясняет появление целого ряда работ на эту тему. Для постановки задачи требуется определить модель процесса, то есть необходимо сформулировать уравнения, начальные и граничные условия, первоначальный вид можно задать в виде петли [5], например можно задать начальные условия магнитного поля, которые зависят от ускорения КВМ [6, 7]:
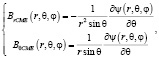
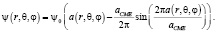 (1)
(1)
Имеется много работ с использованием уравнений идеальной МГД. Распространены также модели, где учитываются диссипативные эффекты:
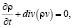
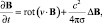
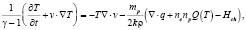
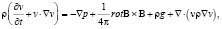
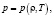
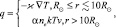 (2)
(2)
где ρ – плотность, v – скорость, B – вектор магнитной индукции, σ – коэффициент электропроводности, T – температура, k – постоянная Больцмана, mp – масса протона, γ – адиабатический коэффициент, ne, np – концентрация электронов и протонов, p – давление, g – ускорение свободного падения, ν – динамическая вязкость, Hch – функция нагрева солнечной короны, Q(T) – функция радиационных потерь, ? – коэффициент теплопроводности, α – постоянная. Даже система уравнений (2) не является полным набором всех МГД уравнений. Решение системы уравнений (2) сводится к нахождению скорости или координат КВМ в виде зависимости или численных значений. При решении возникает ряд проблем, которые связаны с заданием магнитного поля, распределения температуры, плотности, вида функций радиационных потерь и нагрева солнечной короны.
Из-за вращения Солнца и наличия активных областей общее магнитное поле все время меняет свою конфигурацию, поэтому можно использовать только приближенные полуэмпирические зависимости вектора магнитной индукции от времени и координат, одной из главных проблем астрофизики до сих пор является задача нагрева солнечной атмосферы и, соответственно, неизвестны распределения температуры и плотности, а функцию Hch можно только выбирать различными способами, отталкиваясь от конкретной используемой модели, для построения функции радиационных потерь нужно учитывать множество факторов, в том числе химический состав. Также можно упростить систему, если рассматривать полностью ионизованную водородную плазму, тогда функция состояния выглядит так:
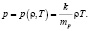 (3)
(3)
Типичным примером подхода на основе идеальной МГД можно считать модели, в которых начальное положение КВМ задается аналитически магнитной трубкой, а окружающая среда представлена в виде упрощенной модели солнечного ветра с учетом эффектов гравитации и дополнительных источников нагрева [5, 6]. Область, в которой разворачивается картина движения, обычно простирается от расстояний порядка 1R? до нескольких десятков и сотен R?.
Более реалистичный подход должен основываться на конкретных данных о КВМ и внешней среде на определенную дату. Необходимо также отметить, что свойство идеальности в некоторой степени является относительным при численном моделировании, поскольку влияние искусственной вязкости способно привести к тем же результатам, которые могут дать вполне реальные диссипативные эффекты.
На рис. 3 и 4 показаны результаты моделирования события от 28–31 марта 2001 г. [7]. Силы, приводящие к замедлению движения КВМ, в данном случае есть силы аэродинамического торможения, магнитного натяжения и гравитационного притяжения. Силы, приводящие к ускорению, – это силы магнитного и газового давлений. На движение может влиять также обмен моментом количества движения с солнечным ветром, особенно значительно этот эффект проявляется при взаимодействии двух различных КВМ.
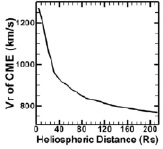
Рис. 3. Изменение скорости КВМ с расстоянием [7]
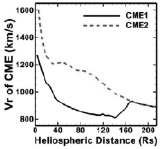
Рис. 4. Иллюстрация процесса взаимодействия двух КВМ [7]
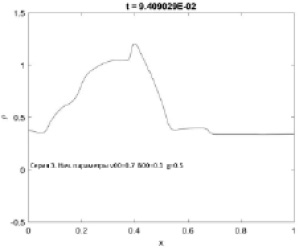
Рис. 5. Начальное распределение плотности вещества в солнечной короне под действием КВМ
В диссипативном приближении широко используются уравнения так называемой термодинамической МГД, в которых учтены вязкость, теплопроводность, электрическое сопротивление, а также излучение и нагрев короны [8, 9]. Для численного моделирования разработан код MAS (Magnetohydrodynamic Algorithm outside a Sphere) с расчетами в сферических координатах, в данном коде используется система уравнений (2). Имеются версии с векторным потенциалом, что освобождает от проблемы выполнения условия 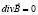 .
.
MAS-код используется при моделировании начального выброса. Для описания движения КВМ в межпланетном пространстве используется его гелиосферная версия, где в уравнении для энергии исключены диссипативные эффекты, нагрев и радиационные потери, но в уравнении для момента количества движения учтены сила Кориолиса и центростремительная сила. При описании движения межпланетных КВМ учитывается также структура межпланетного магнитного поля.
Результаты исследования и их обсуждение
После упрощения системы дифференциальных уравнений для МГД (2) и использования схемы WENO получим распределение плотности в солнечной атмосфере под воздействием КВМ. Благодаря данной схеме погрешности имеют незначительный характер. Задача о динамике облака плазмы решается в приближении двумерной МГД. На плоскости декартовых координат XOY облако задается определенной формы, в данном случае в виде круга. В начальный момент времени облако находится у левой границы области в виде прямоугольника.
Для определения начальных данных потребуется задать распределения плазмы и магнитного поля внутри и вне круга. Распределения внутри круга, описывающие КВМ, будет осесимметричным. Распределение поля вне круга, изображающее внешнее поле, имеет однородный характер на большом удалении от КВМ, то есть от круга.
Заключение
При помощи MAS-кода было проведено моделирование вспышки Бастилия и связанных в ней двух КВМ [9]. Расчеты дали значение скорости, на 200 км/с меньшее наблюдавшейся скорости, что могло привести к задержке времени по прогнозу прибытия КВМ в область околоземного пространства. Одной из возможных причин рассматривается возможность того, что эффекты вязкости и электрического сопротивления в уравнениях МГД оказываются чрезмерными по сравнению с реальными. Таким образом, в результатах моделирования могут появляться артефакты.
Значительные достижения в компьютерном моделировании и разработке технологических решений позволяют развивать следующие задачи:
– численное решение задач динамики корональных выбросов массы (КВМ) на Солнце;
– численное исследование физических эффектов магнитной гидродинамики в динамике КВМ.
Они формулируются как задачи математического программирования, в которых учитываются различные технологические ограничения в виде соответствующих критериев. Основные результаты работы получены на основе современных технологий математического моделирования и численного исследования динамики КВМ.



