Практическая реализация разработанных алгоритмов управления динамическими системами обеспечивается их простотой реализации и понимания, а также гибкостью, устойчивостью, наличием адаптивных свойств, способностью к обучению. Большинство разработанных алгоритмов, базирующихся на теории оптимального и адаптивного управления, не отвечают поставленным требованиям. Кроме того, практическая приемлемость математических моделей, лежащих в основе построения алгоритмов, должна обеспечиваться низкой чувствительностью к изменениям параметров, что для нелинейных систем реализовать достаточно сложно. В последнее время для целей управления все шире начинают применяться методы искусственного интеллекта [1–3]. Интерес к нейросетевому управлению обусловлен прежде всего следующими причинами:
– наличием живых образцов интеллектуальных адаптивных контроллеров – биологических нервных систем;
– способностью нейронных сетей аппроксимировать любые функции [4]. Способность нейронных сетей к самообучению избавляет от необходимости использовать сложный математический аппарат, применяемый во многих традиционных методах адаптивного и оптимального управления; кроме того, способность к самообучению избавляет также от требования наличия большого объема априорной информации об объекте управления, необходимого для реализации методов оптимального и адаптивного управления; Кроме того использование нелинейных функций активации в слоях нейронной сети обеспечивает возможность нелинейного отображения. Данное свойство особенно важно для решения задач управления объектами с существенными нелинейностями, для которых традиционные подходы пока не дают практически реализуемых решений [5];
– высокой степенью параллельности нейронных сетей, позволяющей реализовать очень быстрые методы мультипроцессорной обработки на основе использования нейронных кристаллов или параллельных аппаратных средств [5];
– реализацией архитектуры параллельной обработки, благодаря которой повреждение отдельных технических элементов сети не может существенно влиять на работу сети в целом [5].
В данной работе в качестве объектов управления (ОУ) рассматриваются электроприводы суставов робототехнических систем. Цель управления состоит в обеспечении требуемой точности отработки заданного закона управления в условиях действия внешних дополнительных недетерминированных возмущений гармонического характера, которые могут быть обусловлены следующими факторами [6]:
1) наличием геометрически-силового взаимодействия соседствующих пар координат кинематической цепи робототехнических устройств, обусловленного инерционными, диссипативными и кориолисовыми силами;
2) динамическими нагрузками со стороны объекта или выполняемого технологического процесса;
3) неточностью базирования или неопределенностью расположения технологической траектории в пространстве (случаи, когда фактическая траектория отличается от программной);
4) отклонением параметров ТР от номинальных значений, обусловленным изнашиванием механизмов силовой передачи и движителя, а также изменением климатических характеристик внешней среды.
Материалы и методы исследования
Анализ имеющихся результатов по рассматриваемой тематике свидетельствует об усложнённости конструкций почти всех схем нейроуправления из-за наличия нескольких нейронных сетей (НС) и нетривиальной последовательности процедур их обучения. Кроме того, необходимость процедуры предварительного обучения НС ограничивает применение разрабатываемого контроллера конкретным динамическим объектом, а также ограничивает диапазон изменения параметров объекта и возмущающих воздействий, при которых регулятор обеспечивает требуемые показатели качества. Поэтому перспективным направлением исследований является построение единой управляющей НС, работающей в режиме онлайн-обучения. Можно условно выделить четыре основных подхода нейросетевого управления, применяющих парадигму оперативного обучения в реальном времени [7]:
1. Последовательная схема управления. Нейронная сеть включается в прямой контур управления и обучается отображению желаемых сигналов в управляющие воздействия. В качестве сигнала ошибки, используемого для обучения нейронной сети, применяется сигнал рассогласования между опорным сигналом и фактическим выходом объекта управления. При этом в алгоритм обучения необходимо введение переменной, отражающей динамику объекта управления (якобиан системы).
2. Параллельная схема управления (нейронная сеть служит для компенсации управляющего воздействия, задаваемого обычным контроллером).
3. Схема управления с эмулятором и контроллером (максимизируется некоторая мера полезности и эффективности во времени, однако действительное обучение в реальном времени не достигается из-за медленной сходимости процесса обучения [5]).
4. Адаптивно-критическая схема (приближена к динамическому программированию).
В целом процесс проектирования нейросетевого регулятора можно условно описать следующей последовательностью шагов:
1) определение целей и задач управления;
2) выбор структуры системы автоматического управления (САУ) и типа нейронной сети (НС);
3) выбор алгоритма обучения;
4) обучение НС;
5) моделирование САУ с НС.
Выбор структуры САУ и типа нейронной сети НС
а)
б)
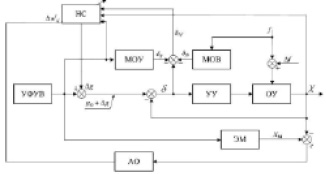
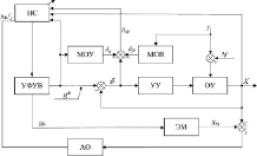
Рис. 1. Структурные схемы САУ с нейросетевым регулятором: а) формирование автономной корректирующей поправки в закон управления; б) коррекция на стадии формирования управляющего воздействия
В качестве базового метода формирования алгоритма управления в САУ динамическими объектами в настоящей работе рассматривается метод комплементарного управления, в основе которого лежит реализация четвертой модифицированной формы инвариантности [6, 8]. Формирование корректирующих поправок для закона управления выполняется методом последовательных приближений, при этом алгоритмы контуров формирования корректирующих сигналов определяются как [6]:
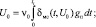
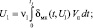
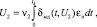
где δмс, δмк, δмд – соответственно статическая, кинетическая и динамическая ошибки по возмущению; U0, U1, U2 – составляющие управляющего воздействия, соответствующие положению, скорости и ускорению сигнала задания;; ν1, ν2, ν3 – коэффициенты передачи в контурах коррекции.
На основе анализа структур САУ с комплементарной коррекцией разработаны две схемы включения нейросетевого регулятора в контур САУ (рис. 2) [9]. Первая структура предполагает формирование НС дополнительной составляющей в управляющее воздействие, обеспечивающей парирование ошибки, обусловленной влиянием внешнего недетерминированного возмущения. Вторая структура предполагает включение НС в процедуру формирования управляющего воздействия в УФУВ.
а) б)
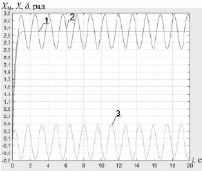
Рис. 2. Характеристики работы САУ в режиме стабилизации: а) характеристики САУ в режиме отработки постоянного задающего сигнала без контура коррекции: 1 – эталонное значение регулируемой координаты; 2 – кривая изменения выходной координаты системы при действии возмущения f(t) = 3sin(4t + 1,57); 3 – ошибка; б) графики ошибок в САУ с контуром коррекции при различных параметрах возмущения:
1 – f1(t) = 5sin(2t + 1,57); 2 – f2(t) = 3sin(4t + 1,57); 3 – f 3(t) = 5sin(4t + 0,7)
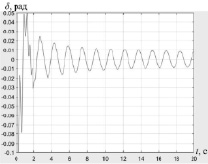
а) б)
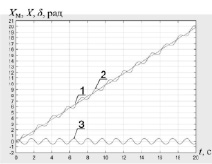
Рис. 3. Характеристики работы САУ в режиме движения с постоянной скоростью: а) характеристики САУ в режиме движения с постоянной скоростью без контура коррекции: 1 – эталонное значение регулируемой координаты; 2 – кривая изменения выходной координаты системы при действии возмущения f(t) = 3sin(4t + 1,57); 3 – ошибка; б) график ошибки в САУ с контуром коррекции
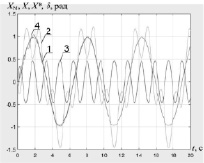
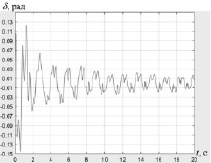
а) б)
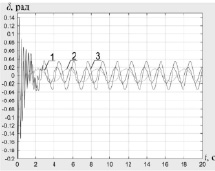
Рис. 4. Характеристики работы САУ при отработке гармонического входного сигнала вида y(t) = sint: а) характеристики САУ при отработке гармонического входного сигнала: 1 – эталонное значение регулируемой координаты; 2 – кривая изменения выходной координаты системы без контура коррекции при действии возмущения f(t) = 3sin(4t + 1,57); 3 – ошибка; 4 – кривая изменения выходной координаты с контуром коррекции; б) график ошибки в САУ с контуром коррекции
На схемах обозначено: УФУВ – устройство формирования управляющего воздействия; УУ – устройство управления; ОУ – объект управления; ЭМ – эталонная модель, обладающая заданными динамическими показателями; МОУ – модель ОУ по ошибке от управляющего воздействия; МОВ – модель ОУ по ошибке от возмущающего воздействия. МОВ и МОУ образованы статическими зависимостями первого и второго коэффициентов ошибки от соответствующего воздействия; НС – нейронная сеть; АО – алгоритм обучения, g0, f – управляющее и возмущающее воздействия соответственно; X, XМ – регулируемая координата и выходная координата эталонной модели соответственно; δ – суммарная ошибка системы; Δf – дополнительное неизмеримое возмущение; δf0, δg – составляющие ошибки системы, обусловленные возмущающим и задающим воздействиями; δΔf – составляющая ошибки, пропорциональная дополнительному возмущению; Δg – дополнительная составляющая управляющего воздействия; ? – ошибка между выходной координатой ОУ и ЭМ. В качестве основного входа нейронной сети выступает ошибка пропорциональная внешнему неопределенному возмущению, выделяемая из суммарной ошибки системы исключением детерминированных составляющих ошибки, получаемых с помощью МОУ и МОВ, а также задержанные значения данного сигнала, определяемые порядком дифференциальных уравнений рассматриваемой динамической системы. Кроме того, в качестве дополнительной информации для обучения НС могут применяться сигналы задающего воздействия и регулируемой переменной. Значимость данных входов НС для процесса формирования корректирующей поправки может быть определена в процессе исследования.
Выделяются три способа идентификации составляющей ошибки, обусловленной влиянием внешнего неопределенного возмущения:
1) использование модели ошибки объекта управления по возмущающему и управляющему воздействиями;
2) использование параллельной прогнозирующей модели;
3) применение блока оценки основных статистических параметров составляющей ошибки системы автоматического управления, обусловленной внешним неопределенным возмущением, и использование данных параметров в качестве входов нейронной сети (данная схема применима для расширения класса рассматриваемых внешних возмущений).
В качестве сигнала ошибки, используемого для настройки весов НС, предлагается использовать сигнал рассогласования между выходной координатой ЭМ и ОУ ?, цель управления – минимизация ошибки в контуре системы. Здесь полагаются неизвестными поправки закона управления, формируемые в контуре коррекции системы, т.е. отсутствие эталонного значения выходного сигнала НС.
В работе [10] доказана универсальная аппроксимационная теорема, обобщающая как результаты А.Н. Колмогорова и Р. Хехт-Нильсена, так и аппроксимационную теорему Стоуна – Вейерштрасса [11]. С точки зрения нейронных сетей ее смысл сводится к тому, что для сколь угодно точной аппроксимации любой функции многих переменных достаточно двухслойной структуры НС при условии, что в скрытом слое использована нелинейная функция активации [12]. Приведенные результаты позволяют сделать вывод о целесообразности рассмотрения для решения поставленной задачи двухслойных НС: входной слой – скрытый слой – выходной слой.
При выборе количества нейронов в скрытом слое можно опираться на методики, изложенные в работе [13]. Для получения нижней оценки количества нейронов в скрытом слое целесообразно использовать результаты, представленные в работе [14], в которой было обосновано, что число нейронов скрытого слоя должно удовлетворять следующему неравенству: Nhid ≥ 2N + 1, где N – это число входов НС.
В большей части работ, посвященных управлению робототехническими системами и различными технологическими процессами, для решения задач управления применяются многослойные нейронные сети прямого распространения, что можно объяснить следующими причинами: 1) такие сети представляют собой структуры с прямыми связями, в которых информация передается от входов к выходам, что особенно удобно для работы с системами, представимыми в виде блоков, в которых сигнал передается последовательно в одном направлении; 2) основной алгоритм обучения таких сетей – алгоритм обратного распространения ошибки, относящийся к широкому классу градиентных методов, часто применяемых в теории оптимального управления [5].
Алгоритм обучения НС
При выборе алгоритма для реализации предложенной схемы обучения следует рассматривать методы последовательного обучения НС, обладающие высокой скоростью сходимости, к таким методам относятся прежде всего методы градиентного спуска первого и второго порядка.
В качестве алгоритма обучения в настоящей работе принят алгоритм обратного распространения ошибки (метод моментов) с регуляризацией [4], в силу простоты его реализации и малых вычислительных затрат. При этом предлагается использовать переменный параметр скорости обучения для каждого слоя НС в функции ошибки нейронов, соответствующего слоя. Алгоритм обучения представляет собой совокупность следующих действий:
1. Инициализировать веса W (случайными малыми значениями), выбрать начальное η0 и максимальное ηmax значения скорости обучения, ошибки управления δ.
2. Инициализировать нулями начальные значения изменения весов ΔW.
3. Определить ошибку E(n).
4. Если результат удовлетворительный, а именно |E(n)| ≤ δ, то обучение сети не реализуется, в обратном случае переход на п. 5.
5. Вычислить значение градиента функции потери ∇E(n) на текущей итерации.
6. Определить параметр скорости обучения для i-ого слоя согласно выражению
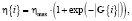
где ηmax – максимальное значение скорости обучения;
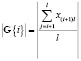– среднее арифметическое значение ошибки для i-го слоя сети; l – число нейронов в j-м следующем относительно i-го слое.
X – матрица ошибок сети, dim(X) =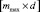 
, где mmax – максимальное значение нейронов среди всех слоев НС; d – число слоев НС. При этом рассматриваем входы сети как первый слой.
7. Вычислить изменение параметров:
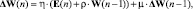
где η – коэффициент, характеризующий скорость обучения; ρ – коэффициент регуляризации; ΔW(n – 1) – изменение весов на предыдущей итерации; μ – коэффициент момента; W(n – 1) – значение весовых коэффициентов на предыдущей итерации.
8. Корректировать веса сети
.
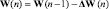9. Переход на п. 3.
Результаты исследования и их обсуждение
Исследование работоспособности рассматриваемой структуры управления было реализовано в пакете Simulink программы MatLab на примере электропривода постоянного тока, расположенного в суставе робототехнической системы. Полагалось, что ОУ подвержен влиянию внешнего неизмеримого возмущения, имеющего вид гармонической функции. В ходе моделирования проводилась оценка точности работы нейросетевого контроллера при типовых видах управляющих воздействий – 1) g(t) = const; 2) g(t) = Vt; 3) g(t) = Asin(ωt + φ) – и изменениях параметров возмущения. На рис. 2–4 представлены кривые, характеризующие работу САУ с применением динамической коррекции, реализуемой нейросетевым регулятором, и без нее. Параметры НС:
1) количество слоев НС – 3;
2) количество входов – 5 (в качестве входов использовался сигнал ошибки, пропорциональный внешнему возмущению и его задержки, а также сигнал задающего воздействия и фактическое значение регулируемой координаты);
3) количество нейронов в среднем слое – 12;
4) функция активации нейронов в среднем слое – логарифмическая;
5) функция активации выходного слоя НС – линейная;
6) алгоритм обучения – алгоритм обратного распространения ошибки;
7) начальный параметр скорости обучения – 0,01;
8) дискретность сети – 0,001.
Анализ результатов исследования при использовании различных функций активации в скрытом слое (сигмоидальной, логарифмической, экспоненциальной, синусоидальной) свидетельствует о том, что наилучшую сходимость процесса обучения обеспечивает применение сигмоидальной и экспоненциальной функций активации. Преимуществом логарифмической функции активации является отсутствие необходимости нормировать входные сигналы, однако в процессе отработки системой гармонического входного сигнала может наблюдаться колебательный характер регулируемой переменной, в некоторых случаях происходит потеря устойчивости.
В ходе исследования была проанализирована точность работы контура коррекции с нейросетевым регулятором на базе двух типов НС c логарифмической функцией активации в скрытом слое: рекуррентной сети и сети прямого распространения ошибки. Анализ результатов свидетельствует, что применение рекуррентных сетей, обеспечивает лучшую скорость сходимости процесса компенсации возмущения, а также меньшие значения ошибки. Однако отсутствие учета динамики объекта управления в формировании алгоритма обучения при отработке гармонического входного сигнала приводит к необходимости включения в цепь формирования дополнительной составляющей коэффициента усиления, обеспечивающего масштабирование выходного сигнала НС, что усложняет процедуру коррекции управляющего воздействия. Поэтому целесо-
образно модифицировать алгоритм обучения с учетом динамики объекта управления. Так как в условиях применения рекуррентной архитектуры НС процедура получения производных от ОУ усложняется, целесообразно также применение сети прямого распространения ошибки.
Анализ точности работы контура коррекции с нейросетевым регулятором с сигмоидальной функцией активации в скрытом слое при отработке гармонического входного сигнала показал большие значения величины рассогласования в контуре системы, чем при использовании НС с логарифмической функцией активации. Однако в данном случае не возникает необходимость в масштабировании выходного сигнала НС, а процесс компенсации устойчив.
Уменьшение времени дискретности НС (что фактически соответствует количеству итераций обучения нейронной сети, приходящемуся на один такт работы системы) приводит к снижению рассогласования выходных величин ОУ и ЭМ при постоянных параметрах НС, поэтому одним из направлений последующей работы является разработка алгоритма определения оптимального параметра дискретности сети.
Результаты исследования также свидетельствуют, что выходной сигнал НС с точностью до коэффициента усиления САУ воспроизводит возмущающее воздействие, то есть предложенные структуры могут применяться также для оценки параметров внешнего неопределенного возмущения при реализации различных алгоритмов управления.
Заключение
Результаты исследования предложенных структур построения систем автоматического управления с нейросетевым регулятором на базе онлайн-обучения свидетельствуют о работоспособности предложенного подхода. Анализ результатов исследования показывает парирование неизмеримого возмущающего воздействия гармонического характера в пределах от 90 до 97 %. Однако отсутствие учета динамики объекта управления при формировании алгоритма обучения нейронной сети приводит к росту ошибки отработки гармонического входного сигнала при полигармонических внешних воздействиях в пределах до 15 % от величины задающего сигнала. Результаты исследования свидетельствуют, что использование логарифмической функции активации в скрытых слоях при отработки системой гармонического входного сигнала требует также включения в контур коррекции звена с коэффициентом передачи 0,01. Кроме того, в ряде случаев наблюдалась потеря устойчивости процесса компенсации. Поэтому целесообразным является применение сигмоидальной функции активации, процесс компенсации при которой во всех проведенных экспериментах устойчив. Дальнейшие исследования будут направлены на разработку модификации алгоритма обучения нейронной сети с учетом динамики объекта управления и алгоритма определения оптимального параметра дискретности сети с целью повышения точностных характеристик предложенных структур.
В целом результаты исследования свидетельствуют о целесообразности применения предложенного подхода формирования закона управления в робототехнических системах, подверженных влиянию внешних недетерминированных возмущений. Однако для полноценной практической реализации необходима модификация алгоритмов, лежащих в основе предложенного подхода, позволяющая улучшить точностные характеристики системы управления.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-08-01126 «а».