При проектировании электроустановок (ЭУ), являющихся компонентами регионально обособленного регионального электротехнического комплекса и других технических объектов, достаточно часто приходится сталкиваться с тем, что эти объекты имеют относительно небольшую предполагаемую длительность использования (типичный пример: осветительные установки). Поиск целесообразного решения основывается на сравнении различных вариантов ЭУ.
Общепринятым [1] является выбор того или иного варианта электроустановки на основе сравнения годовых приведенных затрат. Однако в отдельных случаях может представлять интерес распределение накопленных затрат З на создание и использование ЭУ с течением времени её эксплуатации [2]. Эти затраты включают [3] первоначальные капитальные вложения К1 и годовые эксплуатационные расходы Э. Составляющими К1 является стоимость оборудования и материалов, а также электромонтажных и строительных работ. Основными составляющими Э являются: стоимость электроэнергии, расходуемой на технологический процесс и теряемой в сетях, амортизационные отчисления от капитальных вложений, затраты на текущий ремонт ЭУ, зарплата персонала.
В отличие от К1, которые являются единовременными (иногда распределенными на период строительства), Э являются каждодневными и, постепенно накапливаясь с течением времени, могут превысить значения К1.
Следует также учитывать, что ресурс, заложенный в любой ЭУ, не бесконечен, а иногда и достаточно мал (например, у источников света) [4]. Поэтому наступает момент tР, когда электрооборудование необходимо заменить вследствие его отказа, не поддающегося восстановлению путем ремонта, или вследствие необратимого снижения эффективности [5] (будем называть это событие «исчерпанием ресурса»). Процесс замены влечет за собой новые капитальные вложения К2. Возникает задача учёта случайного характера как самих затрат, так и моментов их вложения.
Цель исследования: определить аналитическое выражение для непрерывной функции математического ожидания предполагаемых накопленных затрат на создание и использование электроустановок с учётом наличия разрывов отдельных реализаций и закона распределения случайной координаты точки разрыва (случайной длительности работы объекта до исчерпания ресурса.
Материалы и методы исследования
Материалом исследования послужили калькуляции затрат на создание и использование электроустановок. Методом исследования явилось математическое моделирование случайной функции накопленных затрат.
При анализе затрат на создание и использование ЭУ следует различать две прогнозируемые функции затрат от времени использования:
1. Фактические затраты, т.е. те затраты, которые имеют место при определенной длительности работы ЭУ до исчерпания ресурса и стабильных расходах на эксплуатацию, например ожидаемые затраты при замене оборудования через один год.
2. Ожидаемые затраты, т.е. затраты при предполагаемой (вероятностной) длительности работы до замены, например ожидаемые затраты при предполагаемой средней продолжительности работы до замены в один год.
По своей вероятностной природе зависимость затрат от времени является случайной функцией [6]. Причиной тому является случайный характер ценообразования в том или ином регионе в тот или иной промежуток времени и случайная длительность работы до исчерпания ресурса. Подобную случайную функцию можно представить в виде семейства реализаций (рис. 1).
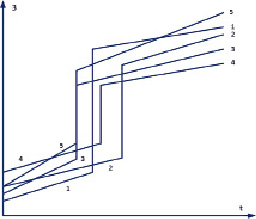
Рис. 1. Накопленные затраты с начала эксплуатации оборудования как семейство реализаций (1–5) случайной функции
Каждую из реализаций (рис. 1, реализация 1–5) накопленных затрат от времени можно назвать фактической. Она позволяет определять распределение затрат с течением времени, если ЭУ была создана и эксплуатировалась, а следовательно, момент замены оборудования точно известен.
Казалось бы, что в качестве времени работы до исчерпания ресурса при прогнозировании затрат можно взять среднее время использования оборудования (средний ресурс), указываемое изготовителем. На самом деле заранее знать момент замены оборудования невозможно, так как он является случайной величиной, распределенной по тому или иному закону распределения вероятностей [7]. Поэтому наряду с фактическими функциями затрат от времени необходимо рассматривать и вероятностные функции, когда ожидаемые затраты определяются с учётом случайной длительности работы до замены.
Для каждой из реализаций характерен различный характер зависимостей затрат от времени на участках непрерывности (он зависит от стоимости электроэнергии и других эксплуатационных расходов, а также от их изменения с течением времени), случайная длительность работы до замены оборудования и случайные первоначальная стоимость и стоимость последующих замен оборудования.
Известно [8], что случайная функция может быть охарактеризована математическим ожиданием (МО), а также дисперсией или средним квадратическим отклонением (СКО). Достоверно определить МО невозможно, но его можно оценить на основе обобщения данных по отдельным реализациям:
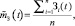
где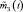 
– оценка МО накопленных затрат, соответствующая длительности периода использования, равной t;
Зi(t) – значение затрат для i-й реализации случайной функции, соответствующее времени t;
n – количество реализаций случайной функции.
Как пример, представлены 5 реализаций случайной функции затрат З (рис. 1) и графически построенная на их основе (рис. 2) ступенчатая линия оценки МО случайной функции.
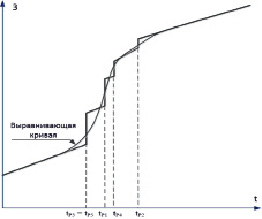
Рис. 2. Обобщающие зависимости (ступенчатая и непрерывная) случайной функции накопленных затрат с начала эксплуатации оборудования
Характерной особенностью последнего графика является наличие точек конечного разрыва, причем их число определяется количеством значений аргумента tР, при которых наблюдаются разрывы отдельных реализаций (в рассматриваемом примере таких точек четыре, т.е. на одну меньше числа реализаций, так как на двух из них разрыв наблюдается при одном и том же значении аргумента). Скачок функции в каждой точке разрыва равен предполагаемым капитальным вложениям на замену исчерпавшего ресурс оборудования.
Возникает вопрос: должна ли также быть разрывной предельная обобщающая зависимость или увеличение количества реализаций в итоге приведет к получению непрерывной функции? Элементарная логика подсказывает, что при наличии разрыва на графике МО затрат диапазон их значений, соответствующих точке разрыва, получен быть не может. Однако совершенно очевидно, что затраты являются непрерывной случайной величиной. Кроме того, из анализа построенного графика (рис. 2) вполне естественно следует, что с увеличением числа реализаций количество точек разрыва обобщающей зависимости будет расти, что в пределе позволяет получить непрерывную функцию З(t) даже в области конечных разрывов отдельных реализаций.
Определим теоретический вид функции З(t) на участке, где наблюдаются разрывы отдельных реализаций.
Будем считать, что имеется n реализаций случайной функции З(t), причем каждая из реализаций Зi(t) имеет разрыв на рассматриваемом интервале времени и может быть описана следующим образом:
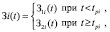
где tРi – точка разрыва i-й реализации;
З1i(t) – вид функции Зi(t) на участке, лежащем левее точки разрыва.
З2i(t) – вид функции Зi(t) на участке, лежащем правее точки разрыва.
Оценка МО случайной функции mЗ(t) для произвольно взятого внутри интервала [tp min); tp max] сечения tj
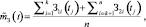
где k – число реализаций, для которых точка разрыва tРi лежит правее рассматриваемого сечения (tj < tРi);
n-k – число реализаций, для которых точка разрыва лежит левее рассматриваемого сечения (tРi ≤ tj);
З1i(tj) и З2i(tj) – значения i-й реализации, соответствующие рассматриваемому сечению.
Преобразуя, получим
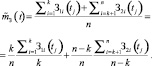
Согласно теореме Чебышева [9], определим МО случайной функции:
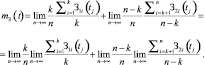
Последнее выражение может быть преобразовано, исходя из условия
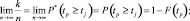
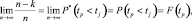
где tР – случайная координата точки разрыва на оси времени;
P*(tР ≥ tj) – статистическая вероятность попадания точки разрыва правее сечения tj;
P(tР ≥ tj) – вероятность попадания точки разрыва правее сечения tj;
P*(tР < tj) – статистическая вероятность попадания точки разрыва левее сечения tj;
P(tР < tj) – вероятность попадания точки разрыва левее сечения tj;
F(tР) – интегральная функция распределения случайной координаты точки разрыва.
Кроме того, при достаточно больших k и n-k
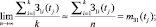
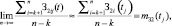
где mЗ1(tj) – МО случайной функции в точке tj при условии, что точка разрыва всех реализаций лежит правее сечения tj;
mЗ2(tj) – МО случайной функции в точке tj при условии, что разрыв всех реализаций наблюдается левее сечения tj.
В итоге после подстановки получим
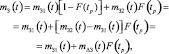
где mΔЗ(t) – МО разности функции З2(t) и З1(t).
Эти выражения получены при условии достаточно больших k и n-k. Однако и при малых k или n-k использование этих выражений вполне допустимо. Это объясняется тем, что малые значения возможны лишь для сечений, лежащих значительно правее МО точки разрыва функций Зi(t), т.е. при выполнении условия tj >> M[tР], где M[tР] – МО точки разрыва реализаций.
Последнее условие предполагает близкие к единице значения F(tp) и, следовательно, mЗ(t) ≅ m2(t).
Аналогично, при малых n-k (то есть при больших k) значения F(tР) близки к нулю, так как соответствующие сечения лежат много левее M[tР], вследствие чего МО случайной функции почти не зависит от значения mЗ2(t):
mЗ(t) ≅ mЗ1(t).
Результаты исследования и их обсуждение
Таким образом, полученные выражения в общем виде описывают функцию mЗ(t) на участке прерывности отдельных реализаций и зависят от закона распределения случайной координаты точки разрыва.
Если предположить, что время исчерпания ресурса tР является случайной величиной, распределенной по нормальному закону, то интегральная функция распределения может быть описана общеизвестным выражением
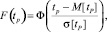
где Ф – нормальная функция распределения, равная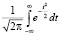 
;
σ[tР] – CKO времени tР.
Тогда общий вид функции mЗ(t) для нормального закона распределения времени tР имеет вид
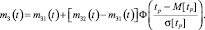
В частном случае, когда МО случайной функции на участках непрерывности линейно зависит от времени перерыва электроснабжения, получим
mЗ(t) = a1t + b1 + (At + B)F(tp),
где a1t + b1 = mЗ1(t);
a2t + b2 = mЗ2(t);
A = a2 – a1;
B = b2 – b1.
В качестве примера (рис. 3) построена функция mЗ(t) с использованием полученного выражения для нормального закона распределения критического времени. В примере заданы следующие параметры:
mЗ1(t) = 20 t + 20; mЗ2(t) = 25 t + 45; M(tР) = 1 год;
σ[tР] = 0 (график 1); σ[tР] = 0,2 (график 2); σ[tР] = 0,1 (график 3);
Для графика 2:
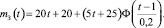
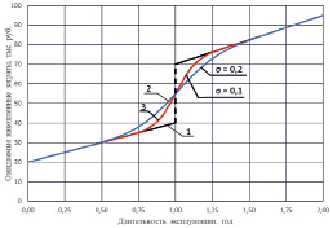
Рис. 3. Функция ожидаемых накопленных затрат З(t) при неслучайном времени исчерпания ресурса (1) и нормальном законе распределения этого времени (2, 3)
При практических расчетах построение подобных зависимостей необходимо осуществлять путем определения неизвестных параметров M[tР] и σ[tР]. Эти параметры возможно оценить на основании статистических данных о длительности работы электрооборудования до замены. Так как сбор такой статистики трудоёмок, искомые параметры можно оценить по данным производителей оборудования. Значение M[tР] приравнивается к средней продолжительности работы (среднему ресурсу). Значение σ[tР] можно оценить, используя «правило 3 σ» [10], определив этот интервал как разность между гарантийным tP ГАР и средним tP СР ресурсами:
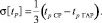
Заключение
1. Накопленные затраты при создании и дальнейшем использовании ЭУ являются случайной функцией времени, реализация которой имет конечные разрывы в точках, соответствующих моментам замены оборудования вследствие исчерпания ресурса.
2. Распределение накопленных затрат при использовании ЭУ зависит от длительности работы оборудования до замены (ресурса), которая является случайной величиной.
3. Получены выражения для определения математического ожидания случайной функции предполагаемых накопленных затрат при распределении длительности работы до исчерпания ресурса по нормальному закону распределения.
Исследование выполнено при финансовой поддержке РФФИ и Правительства ХМАО – Югры в рамках научного проекта № 18-47-860017.